风险中性过程的非参数估计（二）

    二、衍生证券定价

当用连续模型描述基础资产的价格或收益过程时，一般能够给出衍生证券的精确定价形式，但众所周知，连续模型的参数估计相当困难，而且衍生证券一般没有解析形式，通常依赖于一定的数值求解方法。在应用中通常是用离散模型描述基础资产价格或收益过程，然而，在一般情况下，此时只能给出近似的衍生证券定价。刘忠(1998)对此有较详细的叙述。

（一）近似的风险中性定价

假设仍用一阶滞后模型(7)描述基础资产的收益，对于在T时刻到期，且到期时价格为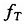的欧式衍生证券，根据引言所述的风险中性定价理论，其在t时刻的价格为





（三）Black-Scholes公式定价

还可以结合一定的参数定价模型来实现定价。比如，如果是对欧式期权定价或美式期权定价，可以将条件方差函数的非参数估计与BS公式结合起来实现定价。

我们知道，BS公式是假设基础资产价格服从几何布朗运动的情形下得到的。尽管对于一般的离散模型(7)，BS公式通常不再是风险中性定价的结果，但是，在许多时候，比如收益的方差是时间的函数时，或者收益的方差是It过程时，BS公式仍然成立或者近似成立，但此时BS公式中的方差应该是期权有效期内中的平均方差。刘忠(1998)对此有较详细的说明。因而，即使是一般的离散模型(7)，对于欧式期权的定价采用BS公式仍然是合理的。

显然，采用BS公式(5)对期权定价时，如果无风险利率已知，方差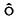就是唯一需要估计的量，而且上述讨论说明，一般情况下应该用期权有效期内的平均方差的估计代替BS公式的。

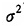当然，最简单的也是最为常用的是将基础资产的历史收益的样本方差作为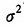的估计，但这忽略了金融数据的条件异方差的个实。另外，历史样本段长度的选取也是没有合理的准则的，也正因为条件异方差性，不同样本段的样本方差可能有较大的差异。这在许多文献中都有说明，比如Rubinstein(1994)。最后，如果是对美式期权定价的话，由于要估计各个时间段内的平均方差，情况可能会更糟糕。

由于参数化模型估计的诸多缺点，采用一给出一些非参数估计是可取的。假设已经得到了收益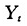的条件方差函数v(x)的估计。不妨假设期权的有效期是从n＋1到n＋T这段时间，获得期权有效期内的平均方差的估计可以有多种方法。

一种方法是逐步预测方法。首先对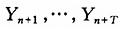进行预测，然后再进行方差的预测。如果期权有效期比较长，这样预测的步数会比较多，实现起来不太自然。





可以看到，基于历史样本方基的BS公式对三种执行价的期权定价都有些偏高，非参数方差估计的定价对平值期权和虚值期权的定价偏低，而对实值期权的定价非参数方差估计的定价要比基于历史样本方差的定价要稍好些。从而非参数估计的定价区间看，都比理论结果（如果假设模拟的理论期权价格服从正态分布）大。

由于在模型(27)下用BS公式定价本身就是近似的，所以两种方法的定价有一定的偏差是可以理解的。另外，这里对模型(27)设定的参数使条件异方差性表现得还不是很强烈，所以非参数方差函数估计的定价比基于历史样本方差的定价的优越性还没有充分体现出来。而且，由于计算速度的原因，这里进行模拟的次数还比较少，更多的模拟结果可能会得到更有说服力的结果。而非参数定价的置信区间一般较大，这是因为非参数估计本身的方差就一般较大，况且这里是对条件方差函数的非参数估计。

所以，从这里的模拟计算看，非参数方差估计的定价是可行的。当然，对于这样的非参数定价，条件方差函数的估计好坏定价结果有很关键的影响。然而，由于条件方差函数的非参数估计还有许多问题没得到很好的解决，所以付诸实践可能还有一段较长的路。

参考文献：

1Cleveland,W.S.and Devlin,S.J.,Locally Weighted Regression:An Approach to Regression Analysis by Local Fitting,J.A.S.A.,83(1988),596-610.

2Duffie,D.,Dynamic Asset Pricing Theory,Princeton University Press,1992.

3Fan,J.,Design-adaptive Nonparametric Regression,J.A.S.A.,87(1992),998-1004.

4Fan,J.,Local Linear Regression Smoothers and Their Minimax Efficiencies,Ann.Statist.,21(1993),196-216.

5Ghysels,E.,Harvey,A.C.and Renault,E.,Stochastic Volatility,Handbook of Statistics.14,Statistical Method in Finance,Edited by G.S.Maddala and C.R.Rao,1996.

6Hardle,W.and Tsybakov,A.,Locally Polynomial Estimates of Volatility Function in Nonparametric Autoregression,Journal of Econometrics,81(1997),223-242.

7Hardle,W.,Lutkepohl,H.and Chen,R.,A Review of Nonparametric Time Series Analysis,International Statistics Review,65(1)(1997).

8Haste,T.and Loader,C.,Locally Weighted Regression,Statistical Science,8(2)(1993).

9Hull,J.,Options,Futures and Other Derivative Securities,2nd Edition,Prentics-Hall,1993.（张陶伟译）

10刘忠.衍生证券定价的非参数方法，华东师范大学一九九八届博士学位论文，1998.

11Robinson,P.M.,Non-parametric Estimation for Time Series Models,Journal of Time Series Analysis,4(1983),185-208.

12Rubinstein,M.,Implied Binomial Trees,Journal of Finance,Vol.LXIX,1994(3)(1994),771-818.

13Wilmott,P.,Horison,S.and Dewynne,J.,The Mathematics of Financial Derivatives,a Student Introductionm,Cambridge University Press,1995.
    责任编辑：夏雨