随机系数离散值时间序列模型（上）

内容提要：本文建立了q阶随机系数整值滑动平均模型。研究发现：固定指标t，该过程服从泊松分布；求得该过程的期望、方差、协方差；证明了该过程是宽平稳过程，均值与协方差均是遍历的；得到了特殊情况下模型参数的矩法估计，该估计是相合估计。通过Monte Calro模拟来验证估计量的优劣。
    关键词：打薄算子 整数值滑动平均模型 随机系数 遍历性
    作者简介：喻开志(1977- )，男，四川成都人，数量经济学博士研究生，西南财经大学统计学院讲师，研究方向：离散值金融时间序列分析、计量经济、消费经济。史代敏(1965- )，男，四川绵竹人，教授、博士研究生导师，西南财经大学统计学院院长，中国统计学会副会长，教育部统计学教学指导委员会委员，研究方向：金融投资数量分析、金融时间序列分析、应用统计。邹红(1982- )，女，湖南娄底人，经济学博士，西南财经大学经济学院讲师，研究方向：消费经济、时间序列分析（成都610074）。
    一、引言
    离散值时间序列数据在现实生活中相当普遍，比如股票的大宗交易、失业数据和不规则金融事件等。但是关于这类数据建模与分析方法最近才发展起来，主要原因是利用传统连续时间序列的相依结构来度量离散值时间序列基本上不可行。关于离散值时间序列数据的建模，众多学者做了有益尝试。比如，Mardia[1](1973)研究了具有Markovian输入的大坝流量问题；Harvey和Fernandes[2](1989)利用状态空间模型建立了计数数据运动模型；Hujer[3]等人(2002)提出了Markov Switching ACD模型来预测金融交易量过程；Ferland，Latour和Oraichi[4](2006)研究了整数值GARCH过程的构建与估计；Andersson和Karlis(2010)[5]研究了整数值自回归过程中缺失数据的填补问题。类似的文献还很多，综合起来大致可以归为三类：①利用转移概率建立相依结构的Markov链模型；②利用潜在过程建立相依结构的状态空间模型；③利用打薄算子建立相依结构的thinning模型。整值滑动平均模型(INMA)属于经典的thinning模型。
    第一个提出INMA模型的是Al-Osh M.and Alzaid A[6](1988)，在用ARMA模型来描述相依泊松计数过程中用到了INMA模型，Brannas和Quoreshi[7](2010)给出了INMA(q)模型参数的条件最小二乘估计、可行最小二乘估计和CMM估计。在这些模型中，变量的系数是常数。受到Zheng，Basawa，Datta[8](2006)关于整值随机系数自回归模型研究的启发，本文提出了一类特殊的整值随机系数滑动平均模型。由于模型的建立需要用到Steutal和Harn[9](1979)定义的“thinning”算子，现在来回顾一下它的定义。
    
    
    
    
    
    
    
    定理5的证明方法比较容易，这里从略。
    

    样本均值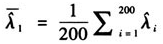、均方根误差。
    
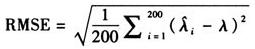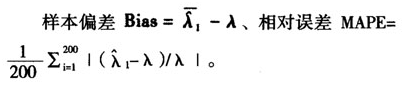
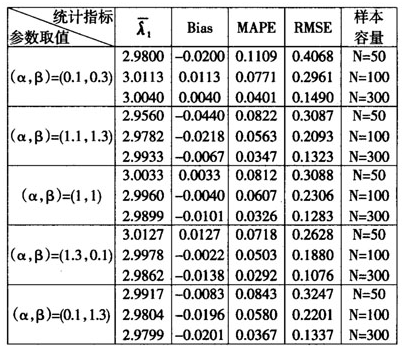
    其中λ表示真实值，具体模拟结果见表1。
    表1λ=3、q=3时，统计量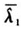、Bias、MAPE、RMSE的估计值
    
    
    

（未完待续）