由于对机制设计理论的开创及发展做出了巨大贡献,赫维茨(Leonid Hurwicz)、马斯金(Eric S. Maskin)和梅尔森(Roger B. Myerson)获得了2007年诺贝尔经济学奖。机制设计理论如今已成为主流经济学的重要组成部分。
一、信息不对称与经济机制
经济理论的一个重要目标是了解什么样的资源配置机制能够最小化由于私人信息而产生的经济损失。什么样的交易机制会实现最大交易收益以及会最大化卖方预期收入?什么样的集体决策程序会成功实施合意的联合项目而否决为不可取项目提供资金?什么样的保险计划会提供最佳保额而不至于被滥用?
机制设计理论,是由赫维茨开创并由马斯金、梅尔森进一步加以提炼与应用的全新理论,为分析与回答这些问题以及其他类似问题提供了有效工具。例如,机制设计理论表明,拍卖在给定的潜在买家间配置私人物品效率最高,同时也能够确定哪种形式的拍卖会给卖家带来最大预期收入。[1][2][3]同样,机制设计理论能够解释为什么市场通常无法解决诸如清新空气、国家安全之类公共品提供的问题,并且能够确认其他更有效率的制度。
在机制设计理论出现之前,资源配置机制的微观经济分析基本上都是关于市场的理论。市场理论的一个核心问题是:市场机制足以有效配置资源吗?市场充分有效需要有非常严格(但不现实)的条件,如市场是完全竞争性的,信息免费获得,只有私人物品,生产与消费没有外部性。而机制设计理论提出了更一般化的问题:资源配置机制在更一般性的条件下能产生最佳结果吗?部分答案是:即使达不到完全有效,市场至少与在不满足完全有效条件下的其他任何机制一样好。例如,双重拍卖(买方和卖方报出买价和卖价)是私人物品交易的常见机制。另一部分答案是市场不适合提供公共品。萨缪尔森(Samuelson)推测资源配置机制不能确保完全有效的公共品供给水平。[4]机制设计理论可以精确地分析萨缪尔森的推测。
赫维茨第一个考虑机制设计问题。他把机制定义为一种信息系统,参与者相互之间或向信息中心传递信息。在这个框架中,市场或类市场的制度可与一系列备择制度相比较。马沙克(Marshak)和日德勒(Radner)的团队理论对机制设计理论做出了重要贡献。[5]在赫维茨1972年引入激励相容的关键概念之后,机制设计理论才获得了广泛应用。[6]激励相容将激励与拥有私人信息参与者的自利结合起来进行严谨分析。随后,显示原理和执行理论对机制设计理论的发展起到了关键作用。第一个系统阐述显示原理的是戈巴德(Gibbard);[7]一些学者独立地将其扩展成贝叶斯—纳什均衡的思想。梅尔森将该原理在一般化方面进行了发展,并开创性地将之应用于规制和拍卖理论等重要领域。[8]然而,显示原理不能解决多重均衡问题,因为最优结果可能在一个均衡点达到,但其他次优均衡也可能存在,参与者有可能选择的是次优均衡。能否设计这样一个机制保证所有均衡都是最优的?马斯金第一个提出了解决该问题的方案即著名的马斯金定理,后来成为执行理论研究的基础,而执行理论是机制设计理论的关键内容。[9]
二、机制设计理论的激励相容、显示原理与执行理论
(一)激励相容和显示原理
最优机制与激励相容这一核心概念有关。为确定最优机制,对于给定的目标函数(如卖方利润或社会福利),首先必须描绘可行机制集,然后明确说明用以预言参与者行为的均衡标准。假设我们关注“直接机制”集,其中行为人报告其私人信息。假定行为人讲的不一定是真话;他们仅在对自己有利的情形下才是诚实的。假定采用占优策略均衡(一个行为人的最优选择和其他行为人的行为无关)作为行为准则,赫维茨将激励相容定义为:如果每个参与者真实报告其私人信息是占优策略,那么这个机制是激励相容的。[6]此外,还要考虑一个参与约束:任何参与主体的福利水平不因参与这个机制而降低。在这种情况下,即使参与者根据自利原则行事,机制也能实现设计者所要实现的目标。在一些弱假设下,赫维茨得出了相反的结论:在一个标准的交换经济中,满足参与约束条件的激励相容机制不能产生帕累托最优结果。[6]换言之,私人信息无法实现完全有效性。
赫维茨的经典研究自然引发这样的疑问:如果考虑到更多类机制或要求不像占优策略均衡那样严格的均衡概念(如纳什均衡或者贝叶斯—纳什均衡),帕累托均衡能否实现?[6]如果不能,社会福利的损失有多大?效率的适当标准是什么?更一般地讲,什么样的机制可以最大化一个给定的目标函数,如利润或社会福利(不论这个结果是否完全有效)?在随后的研究中,这些问题得到了解决,而其中大部分成就要归功于显示原理的发现。
显示原理发现独裁机制的任何均衡结果都可以找到与之相对应的某个激励相容的直接机制。在梅尔森所发展的最一般化理论中,显示原理不仅在行为人拥有私人信息、在采取观测不到的行动(道德风险)时是有效的,在机制有多重阶段时也是有效的。[8]
运用显示原理可将赫维茨的不可能性结果推广到贝叶斯—纳什均衡的情形。[6]因此,在参与者拥有私人信息时,经典意义上的帕累托最优一般是得不到的,需要一种将激励考虑在内的新的有效性标准。如果一种直接机制在激励相容约束下最大化了行为人经加权的预期支付,则称它是激励有效的。以此定义为基础,研究者能够回答源自赫维茨研究中的许多问题。[6]一个关键性问题是市场机制是否是激励有效的。在局部均衡下,梅尔森和萨特瓦特(Saterthwaite)、威尔逊(Wilson)证明了双重拍卖是激励有效的。[10][11]普雷斯科特(Prescott)和汤森(Townsend)对竞争性的一般均衡是激励有效的信息结构特征进行了刻画。在大量模型中,即便没有公共品,经典帕累托有效与自愿参与也是不相容的。在这些模型中,帕累托有效的经典概念通常被相关性更强的激励有效所替代。拉丰(Laffont)和马斯金[12]以及梅尔森和萨特瓦特[10]证明了这一效应的基础性的“不可能结果”,即自愿参与与帕累托有效不相容。
(二)执行理论
激励相容保证了讲真话是一种均衡,但并不能保证它是唯一均衡。许多机制都产生了不同结果的多重均衡。例如,雷宁格(Leininger)、林哈特(Linhart)和日德勒发现双重拍卖有无限多种(实际上是数不清)非线性均衡,这些均衡的福利从激励有效到0。显然,多重均衡降低了双重拍卖的吸引力。[13]
威尔逊分析了可分品的一价拍卖均衡,其中出价者在讨价还价中以非常低的价格拆分商品。在这些“串谋”的均衡中,每一出价者以任何低于其预期均衡份额的价格报价,这种做法阻止了其他出价者获取高于他们(暗中协商的)份额的尝试。这种串谋严重损害了卖方利益。[14]根据克勒门帕(Klemperer)的观点,这种暗中串谋确实给包括英国电力市场在内的许多现实中的拍卖造成了困扰。[15]
社会选择理论也难摆脱多重均衡问题。那些将从许多候选人中选出一个来的投票者,实际上面临着一个合作问题。将票投给几乎没机会赢的人意味着“浪费选票”。如果选举中大家都认为某位候选人没有机会获胜,那这可能成为自我实现的预期。这种现象容易产生多重均衡,其中一些导致了次优结果。
鉴于这些困难,需要设计使所有的均衡结果对于给定目标函数都是最优的机制,这就是众所周知的“执行问题”。格罗伍兹(Groves)和莱亚德(Ledyard)、赫维茨和舒梅勒(Schmeidler)认为,在某些情况下,构建使所有纳什均衡都是帕累托最优的机制是可能的。[16][17]不过,正式的情形是:“弱”执行要求每个均衡都是最优的,而“完全”执行还进一步要求每个最优都是一个均衡。马斯金则给出了纳什均衡社会选择函数的一般性描述。他认为纳什均衡需要一个现在被称为“马斯金单调”的条件。[9]马斯金也说明:如果马斯金单调和被称为“无否决力量”的条件得到满足,若至少有三个行为人,那么纳什均衡的实现是可能的。[9]马斯金在其原稿中对这一结果没有给出完整证明,威廉姆斯(Williams)、瑞普罗(Repullo)、西条(Saijo)后来完整地证明了马斯金定理。[18][19][20]
马斯金在完全信息博弈中考察纳什均衡,但他的结论已被推广到不完全信息博弈中的贝叶斯—纳什均衡。例如,帕尔弗雷和斯瑞瓦斯塔瓦表明,对双重拍卖进行修正可使所有均衡是激励有效的。[21]
马斯金的结论还被拓展到其他许多方面,如虚拟(或近似)执行、“防止重新谈判”均衡中的执行、序列机制路径。[22]执行理论已经并继续在经济学的一些领域发挥重要作用,如社会选择理论、不完备契约理论。
三、机制设计理论的一个应用:双边贸易的贝叶斯机制
许多现实和理论问题都可归结为机制设计问题,如规制、最优税制、民主选举、社会制度设计等。不过,机制设计理论提供的许多震撼人心的结论看起来似乎很抽象,这里以一般商品双边贸易的情形为例来看贝叶斯机制设计分析。
假定某人A拥有一个不可分的物品,A正考虑把这个物品卖给潜在的买方B,物品对A的价值为w,而对B的价值为v。标准化价值v和w以使它们介于0到1之间。如果物品以价格P出售,那么A的效用是p-w,他将放弃对其而言价值为w的物品而获得p作为回报。与此对应,B从这个交易中获得的效用是v-p。如果没有交易发生,各方获得的效用都是0。假定这是一个真实的双边情形,没有一方可以与第三方交易。
在这种情形下,帕累托有效的经典概念要求:如果w<v,卖出物品;如果w>v,则不卖物品。这意味着所有贸易所得应当被实现;从几何上看,当且仅当(w,v)落于图1单位正方形对角线的上方时交易才会发生。现在假定B不知道A的价值,故w是A的私人信息。与此对应,假定v是 B的私人信息。更精确地说,假定A和B这两个人是从具有不同价值的个人总体中随机抽取出来的,在这种方式下,他们的“类型”w和v从统计上来说是不相关且独立分布的随机变量,在整个正方形内,具有正的密度。那么,他们可以用来相互交易的机制是何种类型的?
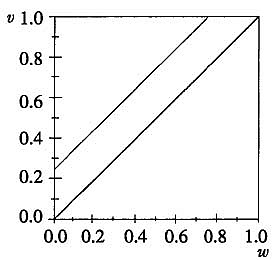
图1帕累托有效的几何示意图
一种可能是A给B提供“要么接受要么放弃”(take-it-or-leave-it)的要约报价;另一种可能性是B给A也提供这样一种要约报价;第三种可能性是双重拍卖,在这种机制中双方(同时)报价,如果B的报价超过A的报价,他们在两个报价之间的某个价格成交(例如,在两个报价的中点处成交)。结果,没有一个机制具有这样的性质:在w≤v的任何时候,交易在均衡下发生。例如,如果A提供一个“要么接受要么放弃”的报价p,则有明确的意图p>w;只有在v≥p时B接受报价。如果w<v<p,交易不会发生,这是一个具有正概率的事件。反之,当B提出要约报价时,情况相同。如果行为人在他们自己的价值上定价,机制将实现所有的贸易利得。然而,这不是激励相容的。行为人A将从高于其价值的定价中获利(目的是获取更高的销售价格);行为人B将从低于其价值的定价中获利(目的是在较低的价格水平下获取物品)。因此,双方愿意不以其真实价值的定价来尝试改善贸易条件。然而这样做他们将不会实现所有的贸易利得。
如果总体价值分布是均匀分布,则双重拍卖存在一个线性贝叶斯—纳什均衡,即在均衡中每一方的买价或卖价随其真实价值上升呈线性增加。更具体地说,在这个均衡中,A的卖价是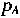

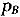
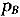
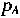
实际上,这种情形很普遍。拉丰和马斯金以及梅尔森和萨特瓦特所确定的不可能结果意味着,对于双边贸易而言,不存在满足参与约束的激励相容直接机制使得当且仅当w≤v时交易发生。[12][10]根据显示原理,可以推断不论如何,不存在能够实现所有贸易利得的机制。而双重拍卖在数学上等价于直接机制,在这种机制中,各方报出自己的价值,当且仅当卖方的价值低于潜在买主的价值时,物品以两个报价之间的价格成交。换而言之,在这个例子中,经典帕累托有效与自愿参与和自由贸易是不相容的。虽然上述均衡结果显然与经典帕累托最优相背离,任何激励相容的机制都不能实现贸易的潜在利得,但可以证明双重拍卖是激励有效的,也可以证明线性均衡达到了有效上边界。利用显示原理,梅尔森和萨特瓦特为贸易利得确立了上边界v-w,它在诸如此类的任何交易机制中都是可实现的。该方法可做如下解释。[10]

式(1)、式(2)这两个不等式就是直接机制的激励相容约束,其中A报价w,B报价v,交易在价格p(w,v)的水平下以概率q(w,v)发生。因此,也可以集中于这样的直接机制——这是显示原理。进一步,如果交易者的预期报酬为负,他将拒绝参与。因此,(事前)参与约束是:

为确定在任意机制下都能达到的贸易利得上边界,只需要考虑能很好定义的数学问题,即:在激励相容和参与约束条件下,最大化预期贸易利得E(v-w)。一个(在某些均衡中)达到这个上边界的机制是激励有效的。梅尔森、萨特瓦特的上边界结果表明由查特吉(Chatterjee)和萨缪尔森首先进行细节研究的双重拍卖是激励有效的。[10][23]
【参考文献】
[1]M. Harris, A. Raviv. Allocation Mechanisms and the Design of Auctions[J]. Econometrica, 1981, (49): 1477-1499.
[2]R. Myerson. Optimal Auction Design[J]. Mathematics of Operations Research, 1981, (6): 58-73.
[3]J. Riley, W. Samuelson. Optimal Auctions[J]. American Economic Review, 1981, (71): 381-392.
[4]P. Samuelson. The Pure Theory of Public Expenditure[J]. Review of Economics and Statistics, 1954,(36): 387-389.
[5]J. Marshak, R. Radner. Economic Theory of Teams[M]. Yale University Press, 1972.
[6]L. Hurwiez. On Informationally Decentralized Systems[A]. Radner, McGuire. Decision and Organization[C]. North-Holland, Amsterdam, 1972.
[7]A. Gibbard. Manipulation of Voting Schemes: A General Result[J]. Econometrica, 1973,(41): 587-602.
[8]R. Myerson. Multistage Games with Communication[J]. Econometrica, 1986, (54): 323-358.
[9]E. Maskin. Nash Equilibrium and Welfare Optimality[J]. Review of Economic Studies, 1999, (66):23-38.
[10]R. Myerson, M. Satterthwaite. Efficient Mechanisms for Bilateral Trading[J]. Journal of Economic Theory, 1983, (28):265-281.
[11]R.
[12]J. Laffont, E. Maskin. A Differentiable Approach to Expected Utility-Maximizing Mechanisms[A]. Laffont. Aggregation and Revelation of Preferences[C]. North-Holland, Amsterdam, 1979.
[13]W. Leininger, P. B. Linhart, R. Radner. Equilibria of the Sealed-Bid Mechanism for Bargaining with Incomplete Information[J]. Journal of Economic Theory, 1989,(48): 63-106.
[14]R.
[15]P. Klemperer. Auctions: Theory and Practice[M]. Princeton: Princeton University Press, 2004.
[16]T.
[17]L. Hurwicz, D. Schmeidler. Construction of Outcome Functions Guaranteeing Existence and Pareto-Optimality of Nash Equilibria[J]. Econometrica, 1978, (46):1447-1474.
[18]S. Williams. Realization and Nash Implementation: Two Aspects of Mechanism Design[J]. Econometrica, 1986, (54):139-151.
[19]R. Repullo. A Simple Proof of Maskin's Theorem on Nash Implementation[J]. Social Choice and Welfare, 1987, (4): 39-41.
[20]T. Saijo. Strategy Space Reduction in Maskin's Theorem[J]. Econometrica, 1988,(56): 693-700.
[21]T. Palfrey, S. Srivastava. Efficient Trading Mechanisms with Pre-Play Communication[J]. Journal of Economic Theory, 1991, (55): 17-40.
[22]H. Matsushima. A New Approach to the Implementation Problem[J]. Journal of Economic Theory, 1988, (45): 128-144.
[23]K. ChatterJee, W. Samuelson. Bargaining under Incomplete Information[J]. Operations Research, 1983, (31): 835-851.^
【原文出处】《经济理论与经济管理》(京)2008年2期第35~39页
【作者简介】杨咸月,上海社会科学院部门经济研究所研究员,经济学博士。上海200020
