政府拨款博弈中拖延和等靠行为：一个模型分析

作者简介：董志强，华南师范大学经济研究所、华南市场经济研究中心副教授，510006。
    一、引言
    在政府部门工作或有过工作经历的人们，已经见惯这样一种现象：上级部门在一些项目上的经费拨款迟迟不到位，或者上级略有拖延但很快就接受了下级申请或拒绝了下级申请；而有些下级会积极地自筹资金去实施其项目，另一些却坚持“等靠要”而不收回向上级伸出的讨钱之手。在一些研究县乡公共财政(比如教育经费)困难的文献中，拨款“拖延”和“等靠要”被视为经费困难的原因之一。
    政府拨款过程中的拖延和等靠行为，通常被人们归因为上级部门工作效率低下或缺乏财力，以及下级懈怠懒惰。不过，效率低下或财力缺乏而导致拖延，以及懈怠懒惰而导致等靠，其道理显而易见，这不足以引起研究者的兴趣。相比之下，如果上级追求工作效率且财力充足，而下级也不懈怠懒惰，此种情况下出现的拖延和等靠就比较令人费解了。而且，如果这种情况确实存在的话，那么政府拨款中的某些拖延和等靠行为就不可能通过提高上级的工作效率和下级的责任心来加以克服，必须对症下药提出另外一些治理对策。
    本文就试图说明，即使上级追求效率且有财力，而下级也并不懈怠，但是拖延和等靠仍是有可能形成的。本文模型的关键假设是上级不知道下级是否有能力以自己的财力实施其项目。由于上级偏好将拨款配置给确实缺乏财力的下级(这样做也更符合效率要求)，它会尝试通过拖延拨款来识别下级的类型。对于确实没有财力的下级来说，没有拨款就无力实施项目，因此它只能在拨款拖延中消极等待，即其等待的机会成本为零。而拥有财力的下级，它可以在以自己的财力实施项目和等待上级拨款来实施项目之间进行选择；但它的等待是有机会成本的——因为任期有限，越是等待则项目实施后在任期内能显示出的政绩越小。正因为不同类型的下级具有不同的等待成本，所以一定条件下上级就可以通过拖延拨款来甄别出下级的类型；或者说，下级对拨款的“等靠要”时间可以传递其类型信号。本文证明，在某种情况下，一定时间的拖延和等靠将是拨款博弈的均衡结果。有趣的是，在我们的模型中除了分离均衡结果外，也存在混同均衡结果和半分离均衡结果。
    当然，任何经济模型都应有其现实基础。与本文模型有关的一个真实案例来自蒲勇健(2004)的一篇评论文章：重庆市曾指令各县级政府对中小学基础设施进行建设、改造和完善，并承诺对建设困难予以拨款资助，但是拨款却迟迟不到位。一些稍有财力的县便自己筹资完成了任务，然后向上级讨拨款，结果却遭到拒绝。这些县以为上级取消了先前承诺的拨款，但是不久却获悉那些根本没有动手改造中小学设施的县最终得到了上级的全额拨款资助。这个例子体现的正是本文模型的分离均衡结果。事实上，本文最初的思想源泉正来自于这一案例。
    本文的学术意义在于：首先，我们对上下级的拨款博弈进行了模型刻画，从而可以较好地解释我们观察到的拨款拖延和等靠行为，以及下级伪装财力困难蒙骗拨款与上级随机拨款的现象；其次，对拖延行为的研究是政治经济学的重要研究议题，虽然经济学中对于拖延行为的研究主要集中在改革政策的拖延中(相关研究综述参见Drazen，2000，Chap.10)，但经济中诸多的策略行为导致的拖延显然也应给予关注，本文则提供了政府在处理经济问题中的拖延行为之一种；尤其是模型表明即使上级没有财力困难而且追求效率，拖延行为也可能因信息不对称而产生，这丰富了我们对于拨款拖延行为的理解。第三，本文也得到了提高上级工作效率之外的促进拨款效率的一些对策性思路。
    二、模型
    考虑上级政府和下级政府(以下简称上级、下级)之间的拨款博弈。一个刚上任的下级试图投资于一个公共项目，该项目产生的社会价值为v，投资需要成本c∈(0，1)。下级的类型取决于其能够分配于该公共项目的财力k，k来自一个规范化的二元随机变量
    
    由于上级不知道下级的具体类型，在某些情况下上级将有动力设计合约去甄别下级的类型；而下级也将有动力传递自己的信号。信息甄别和信号传递之间本质上并没太大区别，主要的差异在于哪一方先行动而已(Dixit和Skeath，2004)。信号传递是掌握私有信息的代理人率先采取行动，信息甄别也无非就是委托人先设计一份合约而且他知道该合约条款可以传递代理人的信息(马可·斯达德勒，佩雷斯·卡斯特里罗，2004)：即信号传递模型和信息甄别模型总可以通过改变参与人顺序而相互转换(Wolfstetter，1999)。因此，本文模型要研究的上级“拖延”行为和下级的“等靠要”行为本质上是一个问题的两个方面，没有上级的拖延也就不会有下级的等靠要(在随后的行文中，“拖延”时间与“等靠要”时间将是同一段时间从两个不同角度的叫法而已)。为了使模型变得简单，我们姑且假设上级政府必定拖延到t＞0的时间长度之后再决定是否拨款；而下级的策略则是要么在时间中一直采取无所作为的等靠要，要么就选择不等待(t=0)而立即实施项目。下级的任期长度被规范化为1，则要求下级等待的时间长度为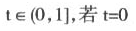是下级没有做任何等待。
    
    是因为如果等待时间越长，离下级任期结束越近，则项目的社会价值越难以在其任期内显示出来作为政绩，比如t=1即在离任时才实施该项目，则根本就没有政绩了；若离任期结束越短，则项目更能在任期内显示其价值，特别地，t=0即没有任何等待，上任就实施该项目，下级离任时将完全获得项目所显示的政绩。
    
    这一点应很容易被理解，给没有财力的下级拨款，而拒绝给有财力的下级拨款，对上级来说应该是最合理的资源配置选择。
    以上的模型假设，可以表示为一个简单的等价博弈树(图1)，其中t＞0的t值假设已由上级事先给定。
    
    该博弈中，赢利是按照各种不同情形根据上下级赢利函数计算出来的。需要特别说明两点：①第二阶段贫困型下级的选择中，只能选择等靠要，原因是它自己根本没有财力，在上级没有拨款时候无力实施项目；
    
    三、模型分析
    图1的拨款博弈将存在分离均衡、混同均衡和半分离均衡。下面，我们逐一进行讨论。
    1.分离均衡
    由于贫困的下级只能选择等靠要，若存在分离均衡，则其中：下级的策略必定是对应于类型
    
    这说明下级等待的最短时间不会突破上级的任期)，以得到充分的信号来判断下级的类型，从而使得其拨款精确地到达贫困的下级手中。而富足的下级预期到这一点，也就不会做无谓的等待，而是上任即立刻实施项目。相反的，如果上级任期较短，如上级很快就会调离或退休，那么就不可能有分离均衡，因为满足分离均衡的t无解(原因是上级自己拖不起时间)。综合上述分析，我们有：
    
    富足的下级不会等靠要，而是立即以自己的财力实施项目；上级观察到下级等靠要(时间至少为t=c/v)后则给予拨款，而观察到下级实施项目则不给予拨款。②如果上级的任期较短，或离任期终止时间较短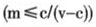，则不存在分离均衡。
    2.混同均衡
    
    若上级不拨款，则富足下级就不会选择等靠要。即上级不拨款将不会存在于混同均衡中。因此，我们集中考察上级选择拨款，即EU(拨款)≥EU(不拨款)的情形。但这又需区分两种情况：
    
    既然t是上级事先决定的拖延时间，从效率角度讲，混同均衡中上级应选择一个非常小的拖延时间t→0。
    
    命题2：当下级属于富足型的概率较小(条件式(3)成立)，而上级拖延时间(或下级等靠时间)t＜min(1-c/v，c/v)时，各种类型的下级都选择等靠要而上级选择拨款的混同均衡是存在的。从效率角度讲，上级拖延(下级等靠要)的时间应是非常之短(t→0)。
    3.半分离均衡
    半分离均衡是这样一种情形：贫困的下级仍只有(惟一的)选择“等靠要”，而富足的下级则以混合策略
    
    
    式(6)表示下级选择等待的预期赢利(等号左边)与选择不等待的预期赢利(等号右边)是一样的；式(7)表示上级选择拨款的预期赢利(等号左边)与不拨款的预期赢利(等号右边)是一样的。对此两式化简，有下级和上级的混合策略解：
    
    ，
    则贫困的下级始终不得不等靠要，而富足的下级以概率选择等靠要；上级在拖延时间到期后以概率选择拨款。这里，τ和y的值由式(8)决定，他们的取值都在区间(0，1)中。
    四、上级的均衡偏好及其选择
    模型中拖延时间的主动权在上级手中，而t的取值对于所达到的均衡有深刻影响，即上级通过操纵t就可导向不同的均衡。如此，则上级必然会操纵以实现最有利于自己的均衡。
    
    
    
    从图2的直观结果中可发现，所以情况可划分为4个区域：①上级任期短，下级富足概率较小，则上级选择混同均衡，此时无论贫穷或富足的下级，都可及时得到拨款；②上级任期短，下级富足概率较大，则上级选择半分离均衡，此时富足的下级将以一定概率选择立即实施项目，以一定概率伪装财政困难申请拨款，而上级也随机地决定是否给予拨款；③上级任期较长，下级富足概率大，则上级选择分离均衡，此时富足下级立即实施项目，上级对等靠一定时间的下级(必为贫困者)给予拨款；④上级任期较长，而下级富足概率较小，这一区域右上部是分离均衡，左下部则是混同均衡，即随着下级富足概率越来越小(x↓)则上级越来越倾向于选择混同均衡(或者实施分离均衡需要的任期m越来越长)——这一点要从区域④中的右下倾斜曲线看出来，这条曲线是分离均衡和混同均衡的分界线。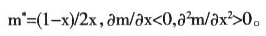
    根据上级的效用函数，可知道模型中的上级是社会效率的追求者，若不考虑上级任期的其他影响，则在本文中给上级一个较长任期而使其可以选择分离均衡，将是最具社会效率的结果。
    五、进一步引申
    本文建立的上下级之间的拨款博弈模型，可以解释上下级政府之间的拨款博弈现象：上级有时会拖延，下级不得不等靠；上级有时拨款又很及时，但是对下级政府是否真的需要拨款却未加详细考察，因此某些有财力的下级也会伪装出财力困难来蒙骗拨款——而且上级任期较短、没有条件拖延拨款的时候这种蒙骗是有可能成功的。本文模型也反映了传统观点的缺陷。传统观点认为拨款拖延主要是上级政府工作效率低下或上级财政困难，而本文模型的结果则表明即使对于一个有财力而且追求效率的高效上级，拖延行为也有可能因信息不对称而产生。这一结论丰富了我们对拨款拖延行为的理解。
    上级究竟会做何决策与下级属于富足型的概率x密切关联，而x与项目的成本和项目的价值v有关。譬如，我们将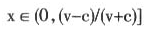为下级富足的概率较小，此时拨款基本上不会被拖延。这里，若v越大或c越小，则显然有x属于“很小”范畴的临界值(v-c)/(v+c)将可以更大。即给定下级类型的概率分布，那么单位投资效益更大的项目，则更容易获得几乎不会拖延的拨款。即若下级希望迅速获得拨款，就应当选择单位投资效益更大的项目。
    模型所表现出的另一个重要观点是：为了保证拨款效率，有必要保证上级政府具有一定的任期长度。上级若是短任期，则只有不拖延一律给予拨款(生活中有一个现象也可由此得到解释，即当一个上级即将离任的时候，总是特别慷慨地满足下级的要求)；由于上级的赢利函数包含了社会资源配置效率的考量，当上级任期够长，可以实施分离均衡的时候，则拨款虽有所拖延，但却保证了资源没有错误配置，拖延的代价可以从资源配置效率得到补偿。这样看来，保证上级具有一个相对下级要长一些的任期将是有积极意义的。事实上，确有一些实际工作者指出，频繁的干部调动也是县乡财政困难的原因之一(吴文军，2004)。
    此外，分离均衡中拖延的时间t=c/v，可以发现越是有价值(v↑)或者越是成本低(c↓)的项目，则均衡的拖延时间也越小。所以要减少拖延时间和等靠时间，那么选择投资效益高的项目仍是重要的因素。现实中大量的拨款拖延和等靠，虽然有可能因上级工作效率而引起，但也完全有可能是因为下级选择的项目投资效益低下所引起。上级的拨款拖延，实际上在一定程度上限制了本已有财力的富足下级仍向上级伸手而投资于缺乏效率的项目。
    诚然，模型中涉及时间但是却没有考虑货币价值的贴现问题。这是因为贴现问题并不是模型的关键问题。如果加入时间上的贴现，那么我们无非是得到分离均衡所要求的上级任期将有所缩短。而且，贴现利率越高，则上级分离下级类型所需要的拨款拖延时间应越短。当然，贴现利率越高也可解释为下级耐心越低，或者解释为社会对资金需要的紧张程度越高。由此而得到的一些结论仍将是很有意义的。
    本文的模型尚存在的一个缺陷是缺乏对上级和下级拨款博弈中谈判动态过程的考察。加入谈判的动态过程可能会得到更深刻的洞见，但是也会使模型复杂很多。这可列为进一步研究的议题。
    参考文献：
    [1]马可·斯达德勒，佩雷斯·卡斯特里罗：《信息经济学引论：激励与合约》，上海财经大学出版社2004年版。
    [2]蒲勇健：《政府拨款博弈：一个眼见的例子》，《经济学家茶座》2004年第14辑。
    [3]吴文军：《多管齐下化解县乡财政困难》，《会计之友》2004年第8期。
    [4]Dixit，A.and Susan Skeath，Games of Strategy.W.W.Norton & Company，2004．
    [5]Drazen，Allan，Political Economy in Macroeconomics.USA：Princeton University Press，2000．
    [6]Wolfstetter，Elmar，Topics in Microeconomics：Industrial Organization，Auctions and Incentives.The Press Syndicate of the University of Cambridge，1999．