内容提要:本文引入“同一时刻各经济体面对的技术前沿各不相同”的假定,改进了现有的数据包络分析方法,并用该方法将1978-2000年中国29个省区市的劳均GDP增长分解为技术效率变化、技术进步和劳均资本积累三个因素的贡献。之后,在Barro回归的基础上,通过控制发展战略的特征,检验了林毅夫归纳的发展战略对资本积累和技术进步影响的两个假说。检验结果表明,中国地区增长的经验事实和假说相容。
关键词:发展战略 经济收敛 中国经济 数据包络分析方法
作者简介:林毅夫,1952年生,经济学博士,北京大学中国经济研究中心教授(北京100871);刘培林,1969年生,经济学博士,国务院发展研究中心发展战略和区域经济研究部助理研究员(北京100010)。
一、导言
劳均产出增长的两个源泉是劳动资本积累和技术进步。在假定各经济体技术进步步伐一样的条件下,新古典经济增长理论得出的推论是,由于资本边际报酬递减,所以初始劳均资本量较少的经济体的劳均资本积累速度,会相对快于初始劳均资本量较多的经济体,进而劳均资本量和劳均收入水平最终收敛。Barro等进一步的研究认为,初始技术水平落后的经济体,在未来的技术进步速度要比初始技术水平先进的经济体快。(注:Robert J.Barro and Xavier Sala-I-Martin,Technological Diffusion,Convergence,and Growth.Journal of Economic Growth,2:1,1997,pp.1-26.)
但是,新古典理论对劳均资本积累和技术进步收敛机制的分析,抽象掉了政府长期经济发展战略以及发展战略所决定的经济结构的影响。与此相对应的经验研究也没有考虑发展战略的影响,无论是Mankiw等(注:N.G.Mankiw,D.Romer and D.N.Weil,A Contribution to the Empirics of Economic Growth.Quarterly Journal of Economics,107,1992,pp.407-437.)、Barro等(注:Robert J.Barro and Xavier Sala-I-Martin,Convergence Across States and Regions.Brookings Papers on Economics Activity,no.1,1991,pp.107-182.and Robert J.Barro and Xavier Sala-Martin,Convergence.Journal of Political Economy,100:4,1992,pp.223-251.)对国际经验和发达国家经验的检验,还是蔡昉等(注:蔡昉、都阳:《中国地区经济增长的趋同与差异》,《经济研究》2000年第10期。以及蔡昉、王德文、都阳《劳动力市场扭曲对区域差距的影响》,《中国社会科学》2001年第2期。)、Jian等(注:T.Jian,J.D.Sachs and A.M.Warner,Trends in Regional Inequality in China.China Economic Review,7:1,1996,pp.1-21.)、Tusi(注:Kai-yuan Tusi,Economic Reform and Interprovincial Inequalities.Journal of Development Economics,50,1996,pp.353-368.)、魏后凯(注:魏后凯:《中国地区经济增长及其收敛性》,《中国工业经济》1997年第3期。)、Cheng(注:Y.Cheng,Regional Growth Dynamics in China:A Re-examination of σ-convergence.and β-convergence.Mimeo,International Workshop on the Chinese Economy.Shanghai,2002.)对中国经验的检验,均是如此。
如果说新古典理论在分析发达的成熟市场经济国家情形时,这种抽象还不至于影响其解释力的话,那么在分析广大发展中国家经济增长的实际情况时,则决不可忽视发展战略的影响。经济发展战略以及由此决定的经济结构是否顺应比较优势,在很大程度上决定着劳均资本积累和技术进步的步伐。林毅夫总结上个世纪,尤其是二战以来的经济史,归纳出发展战略对经济发展影响的若干理论假说,并用国际经验进行了检验。(注:林毅夫:《发展战略、自生能力和经济收敛》,《经济学(季刊)》第1卷第2期,2002年。)刘明兴则用中国的经验检验了林毅夫的假说。(注:刘明兴:《比较优势、工业化与经济增长》,北京大学博士论文,2001年。)但是这些文献和上面提到的其他经济增长的实证检验文献,均有一个共同的特点,即假定技术进步在各个经济体之间是相同的。
假定技术进步速度相同的前提下进行的经济增长收敛实证检验,在一定程度上是误导的。正因为如此,Kumar等、Maudos等以及Gumbau-Albert等新近完成的工作通过数据包络分析的经济增长分解核算框架,将经济增长分解为技术进步(注:技术进步的直观含义是技术前沿的外推;而技术前沿指的是给定投入水平对应的潜在产出。对于技术前沿和技术进步的严格定义,将在后文给出。)和要素积累的贡献,在此基础上,进一步分析要素积累和技术进步各自的收敛效应。(注:S.Kumar and R.Robert Russell,Technological Change,Techological Catch-up,and Capital Deepening:Relative Contributions to Growth and Convergence.American Economic Review,92:3,2002,pp.527-548.and J.Maudos,J.M.Pastor and L.Serrano,Convergence in OECD Countries:Technical Change,Eifficiency and Productivity.Applied Economics,32,2000,pp.757-765.and Mercedes Gumbau-Albert,Efficiency and Technical Progress:Sources of Convergence in the Spanish Regions.Applied Economics,32,2000,pp.467-478.)但是,这些文献所使用的数据包络分析框架面临一个难以解释的结果:“技术有可能退步”。这个结果意味着,在当前时期复制过去时期的生产要素投入结构之后,当前时期的产出水平有可能低于过去时期的产出水平。对这样的分析结果,显然难以从经济学上给出合理可信的解释。正因为如此,Henderson等的论文中,通过对现有数据包络分析框架的改进,避免了“技术有可能退步”的尴尬结果。(注:D.I.Henderson and R.R.Russell,Human Capital and Convergence:A Production-Frontier Approach.University of California,Riverside Working Papers,2001.)
但无论是Kumar等、Maudos等以及Gumbau-Albert等的工作,还是Henderson等的论文,都基于一个共同的假定:“在同一时点上,各经济体面对的技术前沿是相同的”。这个假定事实上是数据包络分析方法一开始赖以发展的基石,但也正是这个暗含的假定导致了两方面的不利后果:(1)限制了该方法在生产率分析方面的运用;(2)测度给定经济体技术效率(注:本文使用的技术效率的含义是,给定投入水平下,实际产出和潜在的最大产出之比。严格的定义将在后文给出。当然,技术效率还可以用给定产出之下,实际投入和潜在的最小投入之比来衡量。)和技术进步时,存在偏差。出于这些考虑,本文放松“各经济体在给定时期技术前沿相同”的假定,构造相应的分析框架。在此基础上,运用1978-2000年期间中国30个省区市的经验资料,对林毅夫归纳的关于发展战略对技术进步和劳均资本积累的影响的两个假说(注:林毅夫:《发展战略、自生能力和经济收敛》,《经济学(季刊)》第1卷第2期,200年。)进行经验检验。本文后面部分的结构安排如下:第二部分将基于本文构造的经济增长分解核算方法,对中国29个省区市在1978-2000年期间的劳均GDP的增长进行分解;第四部分报告了计量检验方程的设定;第五部分报告检验的结果;最后是结论。
二、1978-2000年中国29个省区市劳均GDP增长的分解核算
沿用Henderson等的论文中暗含的“过去掌握的技术不会遗忘”的假定,并引入“各经济体在同一时期面对着不同的技术前沿”的假定,可以构造如下的经济增长分解核算框架。

这个定义的思想与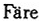 等中的思想(注:R.
等中的思想(注:R.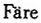 ,S.Grosskopf,M.Norris and Zhongyang Zhang,Productivity Growth,Technical Progress and Efficiency Change in Industrialized Countries.American Economic Review,84:1,1994,pp.66-83.)基本上是一致的。所不同的是这里的定义明确了这样一点:t时期的技术必须使得t以及t以前所有时期的生产行为点可行。显而易见,按照这个定义,即使仅仅有单个经济体时间序列资料的情况下,也可以构造其技术前沿。在这样拟合得到的技术前沿之下,定义该经济体在各时期的技术效率为:
,S.Grosskopf,M.Norris and Zhongyang Zhang,Productivity Growth,Technical Progress and Efficiency Change in Industrialized Countries.American Economic Review,84:1,1994,pp.66-83.)基本上是一致的。所不同的是这里的定义明确了这样一点:t时期的技术必须使得t以及t以前所有时期的生产行为点可行。显而易见,按照这个定义,即使仅仅有单个经济体时间序列资料的情况下,也可以构造其技术前沿。在这样拟合得到的技术前沿之下,定义该经济体在各时期的技术效率为:

上面的(5)式将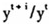 分解为三个因子的乘积,其中前两个因子分别为技术效率变化带来的增长效应(EC)和技术进步带来的增长效应(TP),第三个因子刻画了从时期t到时期t+i之间,投入水平变化带来的产出增长效应(INC)。而前两个因子EC和TP的乘积就是Malmquist生产率。(5)式中的4个产出距离函数
分解为三个因子的乘积,其中前两个因子分别为技术效率变化带来的增长效应(EC)和技术进步带来的增长效应(TP),第三个因子刻画了从时期t到时期t+i之间,投入水平变化带来的产出增长效应(INC)。而前两个因子EC和TP的乘积就是Malmquist生产率。(5)式中的4个产出距离函数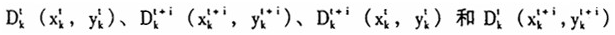 分别通过求解下面的线性规划问题而得到:
分别通过求解下面的线性规划问题而得到:

基于(1)-(7)式构造的方法,我们对1978-2000年期间中国29个省区市(注:由于无法将重庆成立直辖市之前的数据从原来的四川省中分离出来,所以将重庆成立直辖市以后的数据和现在的四川省的数据合并起来,作为一个整体。)劳均GDP的增长的源泉进行分解(注:前面介绍的数据包络分析方法,是在中性规模报酬假定之下,针对总量的生产函数而构造的。这里使用的总量生产函数对应的生产要素包括从业人数、固定资本存量和存货资本存量等三种。但是将要进行分解分析的是劳均产出的增长。这样,集约形式的生产函数对应的生产要素为劳均固定资本和劳均存货资本两种。在总量生产函数满足规模报酬中性的条件下,集约生产函数则呈现规模报酬非递增的特征。在单一产出品的情况下,也即在这里分析的情形下,经由总量生产函数分解得到的技术效率和技术前沿提升对总量GDP增长贡献的测度结果,和经由集约生产函数得到的技术效率和技术前沿进步对劳资GDP增长贡献的测度结果是一致的。所以我们可以运用第三部分的分析框架进行劳均GDP增长的分解核算。)。使用的计量软件是Coelli(1996)给出的数据包络分析专用程序DEAP(注:T.J.Coelli,A Guide to DEAP Version 2.1:A Data Envelopment Analysis(Computer)Program.mimeo,Department of Econometrics.University of New England,Armidale,1996.),分析结果见表1。(注:分析所使用的不变价格总量GDP和从业人数数据,均来自《新中国五十年统计资料汇编》(国家统计局国民经济综合统计司,1999年)和各省区市的统计年鉴。固定资本和存货资本的存量序列,基于《中国国内生产总值核算历史资料1952-1995》(国家统计局国民经济核算司,1997年)和各省区市统计年鉴中报告的固定资本投资和存货资本投资流量数据,运用Harberger(1978年)的方法估算得到1978年的固定和存货资本存量,之后运用永续盘存法估算出各省区市的固定和存货资本存量序列。Harberger的方法参见A.C.Harberger,Perspective on Capital and Technology in Less Developed Countries.In M.J.Artis and A.R.Nobay(eds.),Contemporary Economic Analysis.Croom Helm,1978,pp.15-42。)
上述的分析结果中与直观的印象相违背的是两个西部省区的情形:在本文得到的结果中,青海的技术进步步伐甚至快于山东,而新疆则仅次于山东。青海和新疆的技术进步位于海南和几个直辖市之前。对于这个结果,本文从两方面进行解释。首先,本文测度的技术进步,是各经济体在一定时期的末端年份和起点年份技术前沿的对比,它是各经济体自身时间序列上纵向比较的结果。由于青海和新疆在改革开放之初技术水平就比较低,所以,尽管技术前沿可以迅速提高,但是,其提高之后的技术前沿,仍然要低于其他相对发达的省区市。其次,在概念上要将技术前沿和要素投入水平两者区别开来。一个技术前沿快速提升的经济主体,其实际要素总量和劳均要素总量有可能处于比较低的水平上。其综合作用的结果是,尽管技术前沿快速提升,但是最终的劳均GDP水平也还是比较低。)基于这些结果,下面对两个假说进行检验。(注:严格地讲,发展战略的特征还将影响到技术效率的水平。不过在我们得到的分解结果中,只有湖北一个省的技术效率下降。因而这里仅仅针对技术前沿的提升(即技术进步)进行检验,而不虑及发展战略对技术效率的影响。)
表11978-2000年期间29个省区市总量和劳均GDP增长及其源泉
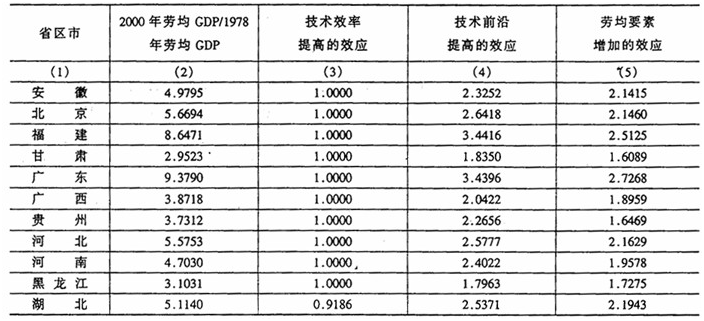
续表1
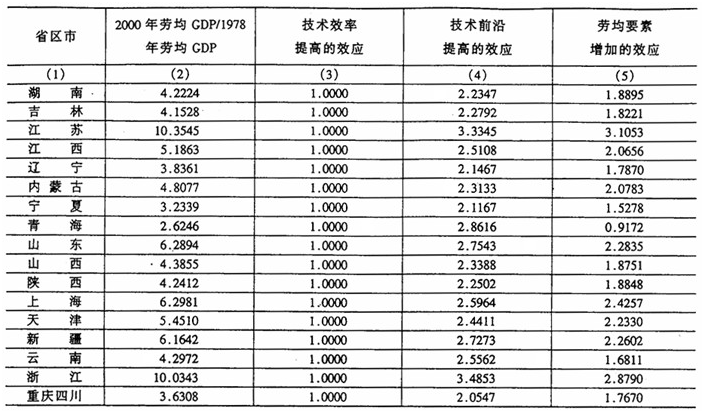
资料来源:根据作者收集的数据集计算得到。
三、计量方程设定
在给出检验的计量方程式设定之前,首先介绍待检验的假说。
(一)两个待检验的假说
假说Ⅰ:经济发展战略对劳均资本积累的影响
当各个经济体按照比较优势战略发展经济,则各经济体之间劳均资本积累符合新古典经济增长理论所刻画的收敛机制;但如果一个经济体优先发展资本密集度超越其所处发展阶段要素禀赋结构决定的最优产业、产品和技术结构,则其劳均要素积累的实际速度会慢于古典收敛机制决定的潜在速度。
假说Ⅱ:经济发展战略对技术进步的影响
在顺应比较优势发展战略的情况下,初始时刻技术落后的经济体通过从先进经济体那里选择适合自身发展阶段比较优势的目标技术进行模仿,可以在未来获得比先进经济体更快的潜在技术进步速度。但如果一个经济体奉行赶超战略,选定的目标技术超前于自身发展阶段的比较优势,技术模仿的成本就高,技术进步的实际速度就会低于潜在速度;该赶超经济体内部各个地区的技术进步速度,也将因为受赶超战略影响的大小而程度不同地减缓,承担赶超任务越重的地区,技术进步速度越慢。
(二)发展战略特征的度量指标
为检验上述两个假说,需要度量发展战略的特征。作者之一构造了实际的技术选择指数(TCI)以及最优的技术选择指数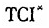 来度量发展战略的特征。(注:林毅夫:《发展战略、自生能力和经济收敛》,《经济学(季刊)》第1卷第2期,2002年。)可以采取如下方式间接度量政府推行的发展战略对于比较优势战略的偏离:
来度量发展战略的特征。(注:林毅夫:《发展战略、自生能力和经济收敛》,《经济学(季刊)》第1卷第2期,2002年。)可以采取如下方式间接度量政府推行的发展战略对于比较优势战略的偏离:

如果一个国家(地区)推行顺应比较优势的发展战略,则DS=0。如果优先发展资本密集度超越所处发展阶段要素禀赋结构所决定的具有比较优势的产业,则这种赶超战略之下DS>0。DS的实际取值越是大于0,则表明赶超力度越大,或者赶超的特征越强。基于这里介绍的发展战略特征的度量指标,下面介绍计量检验的方程设定。
(三)检验假说Ⅰ的方程式设定
针对假说Ⅰ的计量方程式,设定为如下形式:
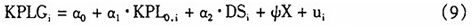
(9)式中,下脚标i代表省区。以及X是各个解释变量;这些解释变量之前的系数,就是待估计的参数;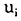 是方程的随机扰动项(注:这两个随机扰动项的分布,我们后面再交待。)。下面介绍方程涉及的变量的含义。
是方程的随机扰动项(注:这两个随机扰动项的分布,我们后面再交待。)。下面介绍方程涉及的变量的含义。
首先介绍因变量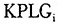 的含义。表1的第(5)列报告了劳均固定资本和劳均存货资本增长对劳均GDP增长的贡献。这个指标是一个无量纲的标量。按照标准增长收敛的方程中线性近似结果,将该结果取自然对数之后得到的值再除以分析时期(1978-2000年)的长度——22年,所得到的最终指标就是
的含义。表1的第(5)列报告了劳均固定资本和劳均存货资本增长对劳均GDP增长的贡献。这个指标是一个无量纲的标量。按照标准增长收敛的方程中线性近似结果,将该结果取自然对数之后得到的值再除以分析时期(1978-2000年)的长度——22年,所得到的最终指标就是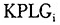 ,其含义是:1978-2000年期间,劳均固定资本和劳均存货资本积累引致的劳均GDP的年平均增长率。(注:在常规的增长收敛估计方程中,因变量是末端年份劳均GDP(或者劳均GDP)的自然对数减去初始年份劳均GDP(或者劳均GDP)的自然对数的差值,再除以所涉及时期的年数。这等于将末端年份劳均GDP(或者劳均GDP)除以初始年份劳均GDP(或者劳均GDP)得到的商,再取自然对数,并再除以所涉及时期的年数。不难理解我们这里定义的因变量和标准做法的定义是类似的,只不过我们定义的因变量中,不包含技术进步对劳均GDP(或者劳均GDP)增长的贡献;而常规做法定义的因变量中包含技术进步对于劳均GDP(或者劳均GDP)增长的贡献。)
,其含义是:1978-2000年期间,劳均固定资本和劳均存货资本积累引致的劳均GDP的年平均增长率。(注:在常规的增长收敛估计方程中,因变量是末端年份劳均GDP(或者劳均GDP)的自然对数减去初始年份劳均GDP(或者劳均GDP)的自然对数的差值,再除以所涉及时期的年数。这等于将末端年份劳均GDP(或者劳均GDP)除以初始年份劳均GDP(或者劳均GDP)得到的商,再取自然对数,并再除以所涉及时期的年数。不难理解我们这里定义的因变量和标准做法的定义是类似的,只不过我们定义的因变量中,不包含技术进步对劳均GDP(或者劳均GDP)增长的贡献;而常规做法定义的因变量中包含技术进步对于劳均GDP(或者劳均GDP)增长的贡献。)
为检验假说Ⅰ当中的收敛机制,需要在(9)式的解释变量中加入初始条件变量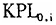 。按照Kumar等、Maudos等和Gumbau-Albert的做法,在我们这里的情形下,应该用各省区1978年的劳均CDP本身作为初始条件变量
。按照Kumar等、Maudos等和Gumbau-Albert的做法,在我们这里的情形下,应该用各省区1978年的劳均CDP本身作为初始条件变量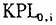 的替代变量。但是假说Ⅰ要检验的收敛机制仅仅是资本边际报酬递减规律作用下,劳均资本拥有量积累带来的收敛效应。而Kumar等、Maudos等和Gumbau-Albert的论文中定义的初始条件变量,则暗含了一个假定:即各个经济体在初始年份的劳均GDP差别,全部来源于劳均资本拥有量之间的差别。显而易见的是,初始时刻劳均GDP差别的原因,除了劳均固定资本和劳均存货资本拥有量的差别之外,还有技术水平(即技术前沿)和技术效率的差别。因此,将技术水平差距和技术效率差距导致的劳均GDP水平差距剔除出来之后,才能更加准确地测度初始时刻劳均固定资本和存货资本拥有量差异引致的劳均GDP水平差异。为此我们尝试在数据包络分析方法的框架之下,将初始年份(1978年)各个省区劳均GDP差异分解为技术前沿差异(
的替代变量。但是假说Ⅰ要检验的收敛机制仅仅是资本边际报酬递减规律作用下,劳均资本拥有量积累带来的收敛效应。而Kumar等、Maudos等和Gumbau-Albert的论文中定义的初始条件变量,则暗含了一个假定:即各个经济体在初始年份的劳均GDP差别,全部来源于劳均资本拥有量之间的差别。显而易见的是,初始时刻劳均GDP差别的原因,除了劳均固定资本和劳均存货资本拥有量的差别之外,还有技术水平(即技术前沿)和技术效率的差别。因此,将技术水平差距和技术效率差距导致的劳均GDP水平差距剔除出来之后,才能更加准确地测度初始时刻劳均固定资本和存货资本拥有量差异引致的劳均GDP水平差异。为此我们尝试在数据包络分析方法的框架之下,将初始年份(1978年)各个省区劳均GDP差异分解为技术前沿差异(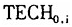 )、技术效率差异,以及劳均固定资本和劳均存货资本差异
)、技术效率差异,以及劳均固定资本和劳均存货资本差异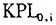 等三个方面的原因。我们以分解测度得到的初始劳均固定资本和劳均存货资本差异
等三个方面的原因。我们以分解测度得到的初始劳均固定资本和劳均存货资本差异 作为初始条件变量。
作为初始条件变量。
发展战略特征由(9)式中的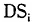 刻画。按照理论预期,如果假说Ⅰ成立,那么初始条件变量
刻画。按照理论预期,如果假说Ⅰ成立,那么初始条件变量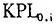 和发展战略变量在方程(9)中系数
和发展战略变量在方程(9)中系数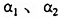 的符号应该显著为负。
的符号应该显著为负。
由于最优的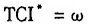 是不可观察的,所以无法直接计算出
是不可观察的,所以无法直接计算出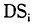 的取值。但是,注意到ω是一个正的常数,在回归分析时,可以将(9)式最终展开为(9')式。
的取值。但是,注意到ω是一个正的常数,在回归分析时,可以将(9)式最终展开为(9')式。
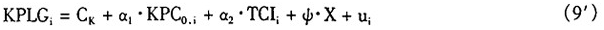
在(9)'式中, 。如果假说Ⅰ成立,那么在(9')式中
。如果假说Ⅰ成立,那么在(9')式中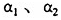 的符号应该为负。
的符号应该为负。
在标准的经济增长收敛计量方程设定形式中,常数项是两个因素的和:(1)技术进步因子;(2)稳态劳均收入乘以初始条件变量系数的绝对值得到的乘积。(注:Robert J.Barro and Xavier Sala-I-Martin,Convergence Across States and Regions,Brookings Papers on Economics Activity,no.1,1991,pp.107-182.and Robert J.Barro and Xavier Sala-I-Martin,Convergence,Journal of Political Economy,100:4,1992,pp.223-251.)我们这里的函数形式中,常数项的含义发生了变化。我们通过数据包络分析方法将Barro回归中的技术进步因子剔除出来(注:在Barro回归方程式的推导中,为了使得稳态增长路径存在,要求技术进步是Harrod中性的。我们运用数据包络分析方法分解出来的技术进步,未必满足这个条件。);同时加入了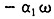 。如果新古典模型的收敛机制成立,而且我们这里的假说Ⅰ成立,则常数项在方程(9')中的估计结果应该为正。
。如果新古典模型的收敛机制成立,而且我们这里的假说Ⅰ成立,则常数项在方程(9')中的估计结果应该为正。
关于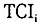 的具体测算办法,请参见中国经济研究中心发展战略研究组(注:北京大学中国经济研究中心发展战略研究组:《关于技术选择指数的测量与计算》,北京大学中国经济研究中心讨论稿,No.C2002003,2002。需要说明的是,由于国家推行的资本密集重工业优先发展战略只能吸收少量劳动力,出于社会稳定等考虑,往往还赋予企业吸收超过必要量的劳动力的社会性政策负担。从而出现一个人的工作三个人干的局面。这和追求资本相对密集产业优先发展的技术赶超是两个概念,两者并不矛盾。因为雇佣同样劳动力数量之下,实际的劳动力利用效率可以大不一样。高就业表象背后实际上是大量的隐性失业。我们这里计算TCI指数所依据的劳动力数量,实际上就高于真实(或者说有效)的劳动力雇佣量。这样一来,就会低估劳均资本装备水平。也就是说,我们得到的TCI指数高估了实际情况。不过这个事实只会加强我们的结论。)。
的具体测算办法,请参见中国经济研究中心发展战略研究组(注:北京大学中国经济研究中心发展战略研究组:《关于技术选择指数的测量与计算》,北京大学中国经济研究中心讨论稿,No.C2002003,2002。需要说明的是,由于国家推行的资本密集重工业优先发展战略只能吸收少量劳动力,出于社会稳定等考虑,往往还赋予企业吸收超过必要量的劳动力的社会性政策负担。从而出现一个人的工作三个人干的局面。这和追求资本相对密集产业优先发展的技术赶超是两个概念,两者并不矛盾。因为雇佣同样劳动力数量之下,实际的劳动力利用效率可以大不一样。高就业表象背后实际上是大量的隐性失业。我们这里计算TCI指数所依据的劳动力数量,实际上就高于真实(或者说有效)的劳动力雇佣量。这样一来,就会低估劳均资本装备水平。也就是说,我们得到的TCI指数高估了实际情况。不过这个事实只会加强我们的结论。)。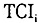 实际上是刻画各个省区的产业、产品和技术结构特征的变量。我们得到的原始数据是各个省区的时间序列数据。因为要刻画1978-2000年整个22年时期里各经济体的发展战略特征,所以比较理想的选择就是将1978-1999年各年份的
实际上是刻画各个省区的产业、产品和技术结构特征的变量。我们得到的原始数据是各个省区的时间序列数据。因为要刻画1978-2000年整个22年时期里各经济体的发展战略特征,所以比较理想的选择就是将1978-1999年各年份的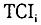 求算术平均。所以我们首先引入了这样定义的TCI7899。
求算术平均。所以我们首先引入了这样定义的TCI7899。
但是,由于TCI7899的分母实际上就是各省区各年度的资本存量除以劳动力存量的比值,所以该指标可能招致这样的误解:TCI7899越高说明其分母项越小,也即该省区总体上的劳均资本越少;而被解释变量正是各个省区的资本积累对经济增长的贡献,理论预期的TCI7899系数的符号为负,自变量和因变量几乎就是同义反复。需要指出的是TCI7899是一个结构变量,TCI7899的分母的确和被解释变量是确定的正向关系,但是TCI7899真正要反映的是给定其分母之后,由于其分子项取值的大小而对资本积累带来的影响。
考虑到这个因素,为了使检验更加稳定(Robust),我们还引入了另外两个定义的发展战略指标:TCI_5_A和TCI7885。前一个指标的定义是1978、1980、1985、1990年和1995年各个省区TCI的算术平均值;后一个指标的含义是1978-1985年各个省区TCI的算术平均值(注:之所以用1978-1985年TCI指数的平均值,是因为以城市经济体制为重点的改革从1985年开始。)。显然TCI7885的外生性更强。如果说围绕TCI7899指数上述误解还在一定程度上值得考虑的话,那么就没有任何理由认为TCI7885和被解释变量存在同义反复的问题。
(9')式涉及的其他解释变量X视具体情况而不同。按照新古典增长理论,储蓄倾向越高的经济体,其稳态劳均产出就越高。这样,如果各经济体之间储蓄倾向不同就会影响到收敛速度。具体来讲,储蓄倾向越高的经济体,经济增长速度就越高。因为其他条件相同的情况下,高储蓄倾向导致高稳态收入水平,进而意味着给定的初始劳均收入和稳态收入之间存在更大的差距,从而就有更快的劳均收入增长速度。所以,我们引入了储蓄倾向(以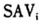 代表)指标。按照新古典增长理论的预期,这个解释变量的系数符号应该显著为正。
代表)指标。按照新古典增长理论的预期,这个解释变量的系数符号应该显著为正。
在具体进行计量估计时,我们模仿Maniw等的做法(注:N.G.Mankiw,D.Romer and D.N.Weil,A Contribution to the Empirics of Economic Growth.Quarterly Journal of Economics,107,1992,pp.407-437.),定义各个省区储蓄倾向为:
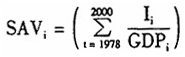
其中分子代表固定资本和存货资本投资(注:我们这里没有考虑政府财政盈余和净出口对于储蓄的影响。毕竟这两者与生产性资本的意义要远一些。这里的储蓄指标的定义,事实上不是特别理想。在新古典模型中运用的是自愿的储蓄倾向,同时暗含了市场出清的条件,从而储蓄自动地全部转化为投资。而我们这里的指标还可以被解释为投资率。而一旦从投资率角度理解这个变量,那么得出的政策含义就应该谨慎对待。毕竟,Solow模型中暗含的自愿储蓄和储蓄自动全部转化为投资的机制,和政府进行赤字政策扩大投资的机制,包含着迥然二致的含义。),分母代表当年的GDP。两者均为当年价格。
另外,在新古典增长模型中,劳动力平均增长率越高的经济体,稳态劳均收入就越低。为此我们引入了各个省区劳动力平均增长率(以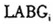 来代表)作为解释变量。按照新古典增长模型的推断,这个解释变量的系数符号应该为负。实际进行计量估计时采用的劳动力平均增长率是各个省区从业人数的年均复合趋势增长率。
来代表)作为解释变量。按照新古典增长模型的推断,这个解释变量的系数符号应该为负。实际进行计量估计时采用的劳动力平均增长率是各个省区从业人数的年均复合趋势增长率。
大量的经济增长收敛回归都将人力资本作为一个解释变量。不过各个研究者实际使用的定义不一样。我们在这里也将各个省区起点时刻的人力资本存量作为解释变量(以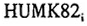 代表)。具体定义是各个省区1982年具有小学文化程度的人口占总人口的比例。
代表)。具体定义是各个省区1982年具有小学文化程度的人口占总人口的比例。
(9')式就是我们最终用来进行计量估计的方程式。方程式中的随机扰动项我们假定存在异方差问题,即:

(四)检验假说Ⅱ的方程式设定和数据
针对技术进步的假说Ⅱ的计量方程式,设定为如下形式:
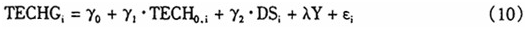
上式中,因变量的含义是技术前沿提高引致的劳均GDP年均增长效应(注:在古典的Solow模型中,稳态路径的存在要求技术进步为Harrod中性的。数据包络分析方法测定技术进步时,并不要求生产函数呈现某个具体形式。这样,我们测定的技术进步未必就符合Harrod中性的要求。在其他类似的文献中,也没有什么办法处理这个问题。)。具体来说就是表1报告的第(4)列数据取自然对数之后,除以22年。
方程(10)中刻画起始时刻技术水平的变量是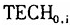 。如果假说Ⅱ成立,那么初始时刻技术水平越高的经济体,在未来的技术进步越慢。所以预期
。如果假说Ⅱ成立,那么初始时刻技术水平越高的经济体,在未来的技术进步越慢。所以预期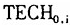 在方程(10)中的系数
在方程(10)中的系数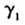 符号为负。Kumar等、Maudos等和Cumbau-Albert的论文在检验技术进步的收敛效应时,用初始劳均GDP本身作为初始技术水平变量
符号为负。Kumar等、Maudos等和Cumbau-Albert的论文在检验技术进步的收敛效应时,用初始劳均GDP本身作为初始技术水平变量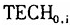 的替代变量。正如前面指出的那样,初始劳均GDP的差距当中,事实上还包含初始劳均资本拥有量差异的影响。所以我们还是沿用数据包络分析方法将初始劳均GDP差距进行分解,以分解之后得到的单纯的初始技术水平差距
的替代变量。正如前面指出的那样,初始劳均GDP的差距当中,事实上还包含初始劳均资本拥有量差异的影响。所以我们还是沿用数据包络分析方法将初始劳均GDP差距进行分解,以分解之后得到的单纯的初始技术水平差距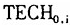 作为方程(10)的初始条件变量。
作为方程(10)的初始条件变量。
上面方程涉及的发展战略特征变量,同样经过和假说Ⅰ的检验方程类似的代数变换,最终得到可以用于估计的计量方程式为:

上面两个方程中涉及的其他解释变量Y,包括人力资本和外国直接投资。人力资本的定义和假说Ⅰ的计量方程中的定义完全一样,不再赘述。外国直接投资(以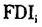 表示),往往意味着先进的管理经验和技术诀窍,所以外国投资越多的省区,则技术进步方面的优势就越大。我们在计量分析中实际使用的外国直接投资指标的定义是:1978-2000年期间外国直接投资累计额的自然对数(注:严格地说,外国直接投资的具体投入形式可能是多种多样的,有现金,有技术股权,有实物作价的资本品等等。国民经济核算角度的总投资定义和外国直接投资的含义不是完全吻合的。从这个角度考虑,通常研究中采用FDI除以投资总额的比例来刻画外资对于经济增长影响的做法,未必妥当。我们认为,从我们主要关注的技术进步角度而言,外资的绝对量要比前述的比例指标的含义更加合适。当然采用这样的定义也暗含地假定,所有来自FDI的技术进步优势,是最初投资时候的一次性贡献。事实上,或许外商投资企业在未来能够分享母公司R&D的进一步信息。也就是说一次FDI带来了持续的技术进步优势。对此我们无法刻画。)。我们预期人力资本和外国直接投资两个解释变量的系数符号应该为正。
表示),往往意味着先进的管理经验和技术诀窍,所以外国投资越多的省区,则技术进步方面的优势就越大。我们在计量分析中实际使用的外国直接投资指标的定义是:1978-2000年期间外国直接投资累计额的自然对数(注:严格地说,外国直接投资的具体投入形式可能是多种多样的,有现金,有技术股权,有实物作价的资本品等等。国民经济核算角度的总投资定义和外国直接投资的含义不是完全吻合的。从这个角度考虑,通常研究中采用FDI除以投资总额的比例来刻画外资对于经济增长影响的做法,未必妥当。我们认为,从我们主要关注的技术进步角度而言,外资的绝对量要比前述的比例指标的含义更加合适。当然采用这样的定义也暗含地假定,所有来自FDI的技术进步优势,是最初投资时候的一次性贡献。事实上,或许外商投资企业在未来能够分享母公司R&D的进一步信息。也就是说一次FDI带来了持续的技术进步优势。对此我们无法刻画。)。我们预期人力资本和外国直接投资两个解释变量的系数符号应该为正。
在(10')式中的随机扰动项,我们假定存在异方差问题,即:
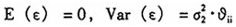
四、两个假说的计量检验结果
基于前述的介绍,我们依次给出假说Ⅰ和假说Ⅱ的计量检验结果。
(一)经济发展战略对劳均资本积累影响的检验
我们运用LIMDEP7.0的计量软件,对方程(9')进行了OLS估计。考虑到截面估计的异方差问题,我们报告了基于White Robust方差协方差矩阵的系数标准差估计。这些结果报告于表2中。
为了和通常的研究所考虑的解释变量进行比较,也为了检验发展战略特征变量(TCI)的稳定性(Robustness),我们估计了8种具体的函数形式。模型Ⅰ是Barro回归的无条件β收敛的方程设定,其中仅仅包含初始条件作为解释变量。初始条件变量的定义在前文已经介绍过,这里不再赘述。我们看到,模型Ⅰ的估计结果在统计上不理想,初始条件变量的系数估计结果的符号为正,与理论预期相背。
无条件β收敛背后的理论依据是资本边际报酬递减。那么模型Ⅰ的估计结果似乎说明在中国资本边际报酬递减规律不成立。但是正如模型Ⅱ—模型Ⅳ所表明的那样,一旦将各省区发展战略特征控制住,就会得到迥然不同的结论。模型Ⅱ当中,除了初始条件变量之外,我们还通过1978-1985年期间各个省区的TCI指数的算数平均值指标TCI7885控制住各个地区的发展战略特征。模型Ⅲ、模型Ⅳ与模型Ⅱ的区别在于控制发展战略特征的变量不同,模型Ⅲ当中用1978、1980、1985、1990、1995年共5个年份的TCI指数的算术平均指标TCI_5_A来控制发展战略特征;模型Ⅳ则用1978-1999年期间各省区TCI指数的算术平均值指标TCI7899来控制发展战略特征。
表2经济发展战略对劳均资本要素积累影响的检验
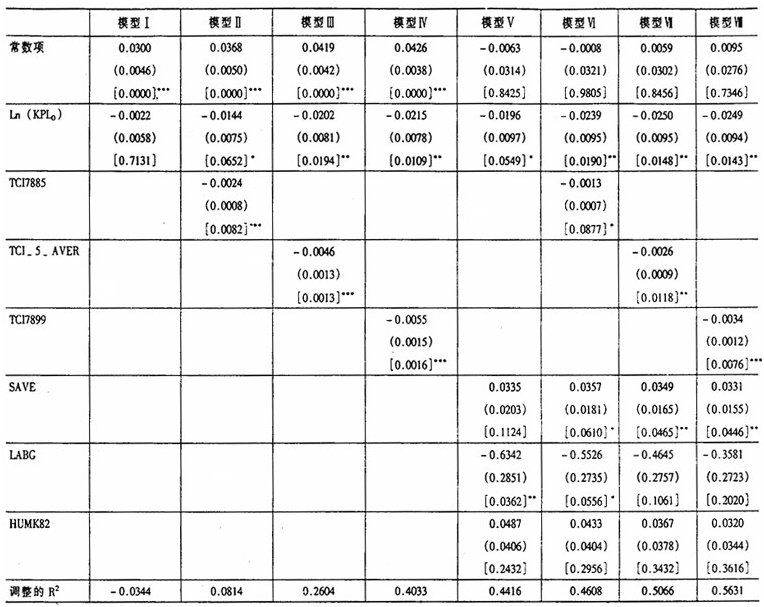
说明:(1) 每个解释变量的系数估计值下面的圆括号里的数字,是系数估计的标准差;再下面的方括号里的数据为“该系数显著异于零”的假说的双尾t检验的p值。以下各个OLS计量结果报告中各个数字含义都与此相同,不再另行交待。
(2) 因为我们假定方程的随机扰动项呈现异方差特征,所以在进行OLS估计时,进行了相应的调整。表中所报告的系数估计值的标准差,是调整之后得到的White Robust方差协方差矩阵。以下各个OLS计量结果都进行了同样的处理,不再另行交待。
(3) 为了直观起见,我们将双尾t检验的显著性水平(p值)小于1%的情形标记为“***”;将双尾t检验的显著性水平(p值)大于1%小于5%的情形标记为“***”;将双尾t检验的显著性水平(p值)大于5%小于10%的情形标记为“*”。以下相同,不再专门说明。
(4) 由模型Ⅱ—模型Ⅳ、模型Ⅵ—模型Ⅷ推算出来的收敛系数β分别为:0.0173、0.0267、0.0291、0.0339、0.0363、0.0361。
从模型Ⅱ—模型Ⅳ的估计结果来看,所有的场合之下发展战略变量和初始条件变量的系数符号均符合理论预期,且双尾t检验均在1%一10%的水平上显著异于零。
另外一旦控制住发展战略特征之后,模型Ⅱ—模型Ⅳ的整体显著性就较之模型Ⅰ大大提高,从调整的可决系数的变化可以看出这一点。由此表明在控制住发展战略特征的条件下,中国1978-2000年期间29个省区的经济增长与无条件β收敛的理论推断相容(注:作者还进行了以1978-2000年期间劳均GDP平均年增长率作为被解释变量的Barro回归,结果表明,当控制住发展战略特征之后,也支持无条件β收敛的理论假说。)。也就是说资本边际报酬递减规律以及发展战略特征共同决定着一个地区的经济增长。
模型Ⅴ当中根据新古典增长理论的分析,引入了初始条件、储蓄率、劳动力增长率和人力资本初始条件等作为解释变量。模型Ⅳ—模型Ⅷ在模型Ⅴ的基础上增加了TCI7885、TCI_5_A和TCI7899作为解释变量。
引入初始条件、储蓄率、劳动力增长率和人力资本初始条件等解释变量之后,模型Ⅴ—模型Ⅷ分别比模型Ⅰ—模型Ⅳ的统计性质发生了根本的改善。初始条件变量和发展战略变量的系数符号符合预期,且其双尾t检验均在1%-10%的水平上显著异于零,整个方程的调整可决系数也大大提高。这在一定程度上说明了条件收敛比起无条件收敛而言,更符合中国实际情况。
储蓄率、劳动力增长率和初始人力资本三个解释变量的符号符合理论预期,但是,除了储蓄率在大多数场合下显著异于零之外,其他两个变量在大部分场合下不显著。对于这些变量揭示出来的信息,我们予以进一步说明。
储蓄率在新古典增长理论中的含义是自愿的储蓄倾向,同时新古典理论模型又假定了储蓄自动全部转化为投资的市场出清假定。但是我们定义的储蓄率实际上是事后的投资率,投资率未必和自愿的储蓄意愿相一致。最容易想见的例子是,存货资本的增加往往是经济周期的反映;而且在许多国有企业执行赶超任务的情况下,因为多生产了不符合市场需要的产品而增加的存货,显然不是社会合意的储蓄行为。更重要的是中国政府在经济中发挥的作用比较大,政府的投资行为在整个社会投资中占有的比例比较大。所以,我们这里的计量结果反映的信息,一部分是自愿的合意储蓄行为的结果,另一部分是其他因素的作用。有鉴于此,应该谨慎对待这里的计量结果的政策含义。新古典模型中社会合意的自愿储蓄行为能够影响长期的稳态收入水平,但是储蓄倾向在较长时期内是稳定的,政府政策对这个因素固然有影响,但影响毕竟是有限的。至于我们的计量结果中蕴涵的政府投资方面的信息,我们的看法是,政府不应该为了提高投资率而采取各种短期的宏观政策增加投资,尤其不应该从赶超目的出发大量投资于资本密集的产业、产品和技术。这样的政策尽管可以刺激短期产出上升,但赶超在短期的有限的正作用,会被TCI指数的反向影响所抵消。
饶有趣味的是劳动力增长率变量的影响。在模型Ⅴ和模型Ⅵ里面,劳动力趋势增长率的系数符号显著为负,在其他情况下均不显著。从业人数的增长包含两方面原因:劳动力随着人口增长的自然增长和劳动力的净流入。新古典增长模型本来要求各个经济体是相对封闭的经济体。一旦考虑到开放条件下的生产要素流动,则收敛速度会加快,因为资本会从相对丰裕(从而资本边际报酬比较低)的经济体,流向资本相对稀缺(从而资本边际报酬比较高)的经济体,而劳动力的流动方向则是从劳动力相对丰裕的经济体流向相对稀缺的经济体。要素流动在新古典增长理论中的直接含义是,各个经济体劳均资本的趋同速度,要比封闭经济条件下来得快,从而劳均产出的趋同速度在开放条件下也比封闭条件下来得快。我们研究的对象是中国的各个省区,这种情形下的要素流动性应该比较强,从而收敛检验所要求的封闭经济条件就不能够满足。不过我们在现实的观察中,并没有看到大量的资本从相对富裕的东部地区流向中西部地区,中国各个省区之间要素流动的主要形式是劳动力从中西部流向东部。这种劳动力流动的作用是使得各个省区之间的劳均资本量更快地趋同,从而使得劳均产出水平的收敛更加迅速。
但是在中国,劳动力流动也许有更加复杂的含义。按照我们的理解,赶超特征越强的省区,劳动力富裕程度就越高,在劳动力流动限制比较严格的情况下,难以流动出来。但一旦劳动力流动的限制逐渐放松之后,赶超特征强的省区里的富裕劳动力,就会流向按照比较优势发展的省区。如果抛开中国的现实情况不论,仅仅在新古典理论设想的没有干预和扭曲的条件下考察劳动力流入东部沿海省区的事实,其含义应该是降低这些流入地的劳均资本提升速度,进而降低其劳均产出增长速度;同时应该使得劳动力流出地省区的劳均资本提升速度和劳均产出增长速度加快。但是,一旦考虑到中国的现实,则结论就大不一样。劳动力之所以从某个地区流出,流入另外一个地区,在很大程度上是因为流出地的赶超特征强,调整存量结构的步伐缓慢,对于劳动力的吸收能力弱,而流入地的赶超特征弱,吸收劳动力的空间大。赶超特征强的省区如果不调整产业、产品和技术结构的话,尽管统计上看从业人数减少了,但是劳均资本积累速度、进而劳均产出增长速度,会低于潜在水平,从而收敛速度还是不能够达到顺应比较优势时的水平。进一步的结论是,尽管赶超特征弱的省区是劳动力流入地,但是其劳均资本和劳均产出的增长速度未必比劳动力流出地的增长速度慢。我们认为这个机制可以在很大程度上解释为什么劳动力增长率变量的系数不太显著的现象。
初始人力资本水平变量的统计性质不理想,尽管系数的符号为正,符合理论预期。当然我们这里得到的仅仅是初始时刻的人力资本。如果资料允许我们控制住整个时期的人力资本特征,或许会得到更加理想的统计结果。所以并不能够从这里的结果中导出人力资本不重要的结论来。
Cheng在评介关于中国地区经济增长收敛性的经验研究文献时指出,经验检验的结果对于京津沪三大直辖市是否包括在样本中比较敏感。(注:Y.Cheng,Regional Growth Dynamics in China:A Re-examination of σ-convergence and β-convergence. Mimeo,International Workshop on theChinese Economy.Shanghai,2002.)为此我们还进行了不包含三个直辖市的数据集的回归。检验表明,数据集当中是否包含三大直辖市对估计结果稍有影响,但没有根本性的改变。我们要检验的假说在包含和不包含三个直辖市的两种数据中,基本上和经验事实相容。另外,作者还将上述介绍的针对方程(9')的8个模型中的初始条件变量,全部用初始的劳均GDP本身作为替代变量,进行了估计,而且分别就包含和不包含三个直辖市两个数据集进行了检验。结果也表明,经验事实和假说Ⅰ相容。对这些结果感兴趣的读者,可以向作者索要有关的结果。
表2报告的估计结果的一个不太理想的性质是,在方程(9')的估计中,模型Ⅴ—模型Ⅷ的常数项的估计结果中甚至出现了负号,和理论预期相反。不过这些估计结果的p值为0.8以上,非常不显著。对于这个现象,我们目前还难以给出合理的解释。而在不包含储蓄率、劳动力增长率和人力资本的模型中,则常数项均显著吻合于理论预期。
需要说明的是,像Kumar等、Maudos等和Gumbau-Albert的论文那样,以初始GDP作为初始条件变量得到的估计结果,和以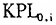 作为初始条件变量得到的估计结果相比,前者条件下初始条件变量的系数估计值的绝对值均小于后者的情形。这个差别的现实含义是,后者情形中收敛速度比在前者情形中来得快。这些现象其实是非常直观的。在我们的分析框架中,落后经济体之所以初始时刻劳均GDP比较低,根源有二:劳均资本比较少;技术水平比较低。相应地落后经济体追赶先进经济体的途径就有二:(i)凭着资本边际报酬递减规律而以较之先进经济体更快的速度积累劳均资本;(ii)凭着技术模仿的低成本优势而以较之先进经济体更快的速度改进技术。我们要检验的假说Ⅰ是这里的途径(i),所以,以
作为初始条件变量得到的估计结果相比,前者条件下初始条件变量的系数估计值的绝对值均小于后者的情形。这个差别的现实含义是,后者情形中收敛速度比在前者情形中来得快。这些现象其实是非常直观的。在我们的分析框架中,落后经济体之所以初始时刻劳均GDP比较低,根源有二:劳均资本比较少;技术水平比较低。相应地落后经济体追赶先进经济体的途径就有二:(i)凭着资本边际报酬递减规律而以较之先进经济体更快的速度积累劳均资本;(ii)凭着技术模仿的低成本优势而以较之先进经济体更快的速度改进技术。我们要检验的假说Ⅰ是这里的途径(i),所以,以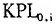 作为初始条件变量进行估计,所得到的收敛系数反映的就是单纯资本边际报酬递减规律的作用机制。而一旦将初始条件变量定义为是1978年劳均GDP的自然对数,那么实际上是误导的,这个替代变量的含义不是纯粹的,其中还包含着技术水平和技术效率差异带来的影响。因为初始时刻劳均GDP较少的经济体,往往技术水平和技术效率低下,所以,Kumar等、Maudos等和Gumbau-Albert的做法等价于这样的含义:劳均资本的积累除了要追赶劳均资本量本身的差别以外,还要追赶初始时刻技术水平和技术效率方面的差距。换言之,按照Kumar等、Maudos等和Gumbau-Albert的做法估计得到的收敛系数,实际上还包含了将初始时刻的技术水平和技术效率等方面的差距弥补到起始时刻先进经济体那样高的水平上的任务。从这个角度可以看出,我们运用数据包络分析方法将初始年份劳均GDP差异分解为劳均要素拥有量差别的效应和技术水平差别的效应,对于问题的理解是有意义的,从而丰富了这方面的经验研究文献。
作为初始条件变量进行估计,所得到的收敛系数反映的就是单纯资本边际报酬递减规律的作用机制。而一旦将初始条件变量定义为是1978年劳均GDP的自然对数,那么实际上是误导的,这个替代变量的含义不是纯粹的,其中还包含着技术水平和技术效率差异带来的影响。因为初始时刻劳均GDP较少的经济体,往往技术水平和技术效率低下,所以,Kumar等、Maudos等和Gumbau-Albert的做法等价于这样的含义:劳均资本的积累除了要追赶劳均资本量本身的差别以外,还要追赶初始时刻技术水平和技术效率方面的差距。换言之,按照Kumar等、Maudos等和Gumbau-Albert的做法估计得到的收敛系数,实际上还包含了将初始时刻的技术水平和技术效率等方面的差距弥补到起始时刻先进经济体那样高的水平上的任务。从这个角度可以看出,我们运用数据包络分析方法将初始年份劳均GDP差异分解为劳均要素拥有量差别的效应和技术水平差别的效应,对于问题的理解是有意义的,从而丰富了这方面的经验研究文献。
(二)经济发展战略对技术前沿提升影响的检验
表3经济发展战略对技术进步影响的检验
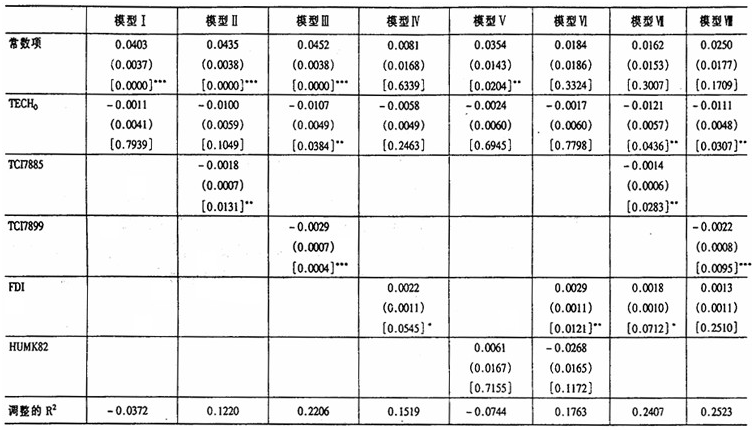
表3报告了假说Ⅱ的检验结果,所给出的系数估计的标准差是White Robust方差协方差矩阵的系数标准差估计。我们估计了8种模型。
从模型I的估计结果来看,技术落后经济体在技术进步方面的后发优势,在中国并不是无条件成立的。在模型Ⅱ和模型Ⅲ当中,我们分别引入了发展战略特征的变量TCI7885和TCI7899。在前面检验劳均资本要素积累时控制发展战略特征的比较理想的变量为TCI7899,但是在那里这个变量的分母和被解释变量同方向变化,所以需要就发展战略特征尽可能地进行Robust的估计。但是在这里检验技术前沿提高和发展战略之间的关系时,没有任何先验理由可以认为1978-1999年22年的TCI指数的平均值TCI7899和被解释变量(即技术进步)之间存在系统性关系。从这个角度来讲,TCI7899是反映发展战略的比较好的指标。不过我们还是估计了以TCI7885为发展战略控制变量的模型。
从模型Ⅱ和模型Ⅲ的估计结果来看,初始技术水平变量以及发展战略特征变量的系数符号均符合理论推断,除初始技术水平变量的系数在模型Ⅱ中的p值为0.1049以外,其他场合下初始技术水平变量和发展战略指标的系数估计值的双尾t检验均显著异于零。
模型Ⅳ和模型Ⅴ在模型Ⅱ的基础上,分别引入了外国直接投资(FDI)和初始的人力资本水平(HUMK82)作为解释变量;模型Ⅵ则同时引进两者作为解释变量。从这里的估计结果来看,FDI变量的系数符号符合预期且显著。但是初始人力资本变量的系数在有些场合下为负,与通常的直觉相背。当然,造成这种情况的原因可能是我们定义的人力资本本身的数据质量不高,所以难以从中归纳出人力资本对技术前沿提高起反向作用的一般性结论。
模型Ⅶ和模型Ⅷ在模型Ⅵ的基础上分别引入了TCI7885和TCI7899作为解释变量。估计结果表明,发展战略变量本身的系数符号均显著为负,双尾t检验的显著性水平分别为5%和10%。初始技术水平变量的系数符号也均稳定地为负,且在5%显著性水平上异于零。
我们还进行了不包含三个直辖市的数据集的回归,检验结果没有根本的变化,要检验的假说在包含和不包含三个直辖市的两种数据中,基本上和经验事实相容。另外,作者还将上述介绍的针对方程(10')的8个模型中的初始条件变量,全部用初始的劳均GDP本身作为替代变量,进行了估计,而且分别就包含和不包含三个直辖市两个数据集进行了检验。结果也表明,经验事实和假说Ⅰ相容。对这些结果感兴趣的读者,可以向作者索要。
以初始GDP作为初始技术水平的替代变量的估计结果,和以初始技术水平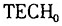 作为初始条件变量的估计结果相比,初始条件的系数估计值的绝对值,在后者情形中均大于在前者情形中的结果。这个对比关系的现实含义是,后者情形中的后发优势比在前者情形中来得更大。在方程(10')中,以纯粹技术前沿相对水平作为初始变量,则我们得到的后发优势变量的系数就是单纯技术模仿成本小于自己创新成本的规律的作用。而当我们将方程(10')中的初始条件变量替换为1978年劳均GDP时,事实上还把由于劳均资本要素拥有量差别以及技术效率差别对初始时刻劳均GDP的影响也包括进来。因为初始时刻劳均GDP较少的经济体往往劳均资本量少、技术效率低下,所以,以1978年劳均GDP自然对数作为初始条件变量进行估计所得到的后发优势系数,实际上还包含了这样的含义:技术模仿成本低下带来的快速的技术进步除了要追赶技术水平本身的差距之外,还要将初始时刻劳均资本量低下等方面的差距弥补起来。由此可见,运用数据包络分析方法将初始年份的劳均GDP差异分解为劳均要素拥有量差别的效应和全要素生产率水平差别的效应,深化了对问题的理解。
作为初始条件变量的估计结果相比,初始条件的系数估计值的绝对值,在后者情形中均大于在前者情形中的结果。这个对比关系的现实含义是,后者情形中的后发优势比在前者情形中来得更大。在方程(10')中,以纯粹技术前沿相对水平作为初始变量,则我们得到的后发优势变量的系数就是单纯技术模仿成本小于自己创新成本的规律的作用。而当我们将方程(10')中的初始条件变量替换为1978年劳均GDP时,事实上还把由于劳均资本要素拥有量差别以及技术效率差别对初始时刻劳均GDP的影响也包括进来。因为初始时刻劳均GDP较少的经济体往往劳均资本量少、技术效率低下,所以,以1978年劳均GDP自然对数作为初始条件变量进行估计所得到的后发优势系数,实际上还包含了这样的含义:技术模仿成本低下带来的快速的技术进步除了要追赶技术水平本身的差距之外,还要将初始时刻劳均资本量低下等方面的差距弥补起来。由此可见,运用数据包络分析方法将初始年份的劳均GDP差异分解为劳均要素拥有量差别的效应和全要素生产率水平差别的效应,深化了对问题的理解。
五、结论性评论
本文对比较优势发展战略理论的两个理论假说进行了经验检验。结果表明,两个理论假说和中国1978-2000年期间29个省区的劳均GDP增长的经验证据相容。归纳起来,有下面几个结论:
因为资本边际报酬递减规律的作用,在顺应比较优势战略从而没有扭曲的情况下,初始劳均资本量较少的经济体在未来时期劳均资本积累的潜在速度,较之初始劳均资本量较多的经济体来得更快;而违背比较优势的发展战略,将使得实际的劳均资本积累速度低于潜在速度。
技术落后经济体顺应比较优势战略,从先进经济体那里选择适合落后经济体自身发展阶段的适用技术进行模仿,所花费的成本低于自己研发这些技术的成本,所以初始技术水平较低的经济体根据自身要素禀赋结构的动态变化,确立适当的目标技术进行模仿,在未来时期潜在技术进步速度可以较之初始技术先进经济体更快;而违背比较优势的发展战略将使技术进步的实际速度低于潜在速度。
综合起来,初始劳均收入水平较低的经济体,通过确立适当的目标技术进行模仿,可以在未来时期获得较之初始劳均收入水平较高经济体更快的劳均GDP潜在增长速度。但是违背比较优势的发展战略则会使劳均收入实际增长速度低于潜在速度。
经济学
经济发展战略对劳均资本积累和技术进步的影响——基于中国经验的实证研究
http://www.newdu.com 2018/3/8 《中国社会科学》(京)2003年04期第18~32页 林毅夫 刘… 参加讨论
Tags:经济发展战略对劳均资本积累和技术进步的影响
责任编辑:admin相关文章列表
没有相关文章
[ 查看全部 ] 网友评论
没有任何评论