内容提要:基于纳什合作博弈议价理论,研究劳动分工对收入分配影响的多重性发现:当生产者之间的总体生产效率差异过大时,进行分工合作的利益基础会消失,收入差距会达到最大的状态。在分工条件下,生产者之间的收入差距取决于高技能生产者的总体优势强度;但分工条件下的收入差距小于自给自足下的收入差距,劳动分工具有缩小收入差距的效应。当生产者各有所长,总体优势相当,是完全“互补型”时,则平分分工产品,高效率与高公平同时实现,是一种最理想的分工经济。结论表明,“公平与效率相统一”在一定条件下可以实现。要实现经济的又好又快增长,政府应当进行以分工为基础的发展制度创新。
关键词:劳动分工,收入分配,利益关系
该标题为《改革》编辑部改定标题,作者原标题为《劳动分工对收入分配的影响研究》。基金项目:2010年度国家软科学重大招标项目“城乡统筹与农村生活形态变化研究”(批准号:2010GXS1D094)、国家社会科学基金项目“推进中国农村流通现代化研究”(批准号:09XJY031)。
解决收入分配的公平性问题是我国“十二五”时期的重要任务。“劳动分工是促进生产率提高的最主要因素”[1]。劳动分工在促进总产出增长的同时,对人们的收入分配又会产生怎样的影响呢?国内外学者从宏观层面和微观层面进行了探索。
在宏观层面上,学者们认为劳动分工会促进收入分配公平。Turgot认为,劳动分工的发展,会带来社会最底层成员生活水平的提高[2]。Smith(1776)在《国富论》中论及了分工与普遍富裕的关系,“在一个政治修明的社会里,造成普及到最下层人民的那种普遍富裕情况的,是各行各业的产量由于分工而大增。各劳动者,除自身所需外,还有大量产物可以出卖;同时,因为一切其他劳动者的处境相同,各个人都能以自身生产的大量产物,换得其他劳动着生产的大量产物,换言之,都能换得其他劳动者大量产物的价格。别人所需的物品,他能予以充分供给;他自身所需的,别人亦能予以充分供给。于是,社会各阶级普遍富裕。”Emile Durkheim认为,劳动分工最大的功能在于促进社会的“有机团结”,增强社会成员之间的有机联系,从而对社会成员收入差距的扩大产生制约[3]。陈宗胜研究认为,当经济发展推进到现代经济占主导地位时,经济中的产业、行业、专业职业等更加多样化,分工更加细密,这时大多数经济活动都需要复杂劳动,对简单劳动需求减少,会使劳动的差异性在更高基础上缩小,由此制约的相对收入差别也会减小[4]。以上这些文献从宏观上分析了劳动分工促进收入分配公平的可能性,但没有清楚地揭示出劳动分工促进收入分配公平的实现条件。
在微观层面上,学者们认为当劳动者之间生产函数和比较优势存在差别时,分工收益是不平等。Yang比较分析了有限个局中人进行劳动分工的纳什议价均衡与瓦尔拉斯均衡,发现各局中人的生产函数事前不相同时,在纳什议解均衡状态下,分工好处在各局中人之间分配是不平均的,但是在收益趋于零时,收入分配趋于平等的意义上纳什议价解均衡显示了它的公平性,是帕累托最优的;而瓦尔拉斯均衡可能导致分工收益的很不平等,产生内生交易成本,结果是一个帕累托无效的分工水平[5]。陆铭、陈钊和杨真真基于纳什议价解建立了包含收益递增的策略性劳动分工模型,论证了按照静态比较优势分工的劳动产品分配是不平等的,而策略性劳动分工甚至会导致人们有时不选择分工,产生分工的效率损失;社会产出更平等的分配可能引导低技能者顺应当前的比较优势而进行专业化分工,从而有利于经济增长[6]。以上这些文献分析了分工条件下收入分配的不平等问题,但同样没有揭示产生不平等的约束条件,同时也缺少对劳动分工与自给自足条件下收入分配不平等的对比分析,而这些问题对全面理解劳动分工与收入分配的关系是极其重要的。
这里通过建立具有外生比较优势的两人两产品劳动分工模型,以自给自足为参照,用纳什议价解来分析劳动分工与收入不平等的关系,其目的在于揭示劳动分工影响收入分配的机制,分析劳动分工促进收入分配公平的实现条件,并对比研究劳动分工与自给自足条件下收入分配的不平等程度。
一、劳动分工与收入不平等关系的理论模型
(一)模型环境描述
假设一个经济体只有两个行为人,一个是低技能生产者(行为人1),另一个是高技能生产者(行为人2)。每个生产者同时也是消费者。有两种消费品X和Y都是必需品,两生产者对X和Y产品的生产量为Xi和Yi,i=1,2。两生产者对X和Y产品的消费量为 和 ,i=1,2。两生产者的效用为Ui,i=1,2。为简化计算,两行为人的总劳动时间标准化为2, 和 分别为投入X和Y产品的生产时间,i=1,2。两生产者的效用函数为:

低技能生产者的生产函数为:

高技能生产者的生产函数为:
式(2)中的a1、a3分别为低技能生产者生产Y和X产品的单位劳动生产率;式(3)中的a2、a4分别为高技能生产者生产Y和X产品的单位劳动生产率。为进一步简化计算,将低技能生产者的劳动生产a1、a3标准化为1。低技能生产者生产两种产品的效率总体低于或不超过高技能生产者,因此a2a4≥1。为了明确分工中的生产产品定位,进一步假定高技能生产者在生产X产品上有绝对优势,令a4>l,且a4≥a2。便于比较生产优势的强弱程度,令 η具有两层含义:一是在a4一定的条件下,η可以看成高技能生产者的总体优势强度系数,η越大,表明高技能生产者的总体优势越强(也即a2a4的值越大);二是η反映高技能生产者相对低技能生产者在两种产品上的优势差异程度,η越大,这种差异越小,极端地η=1,说明高技能生产者相对低技能生产者在两种产品上具有相同的优势;η越小,说明高技能生产者相对低技能生产者在Y产品上优势越弱。利用η与劳动分工的关系,可以检验李嘉图的比较优势理论。
η具有两层含义:一是在a4一定的条件下,η可以看成高技能生产者的总体优势强度系数,η越大,表明高技能生产者的总体优势越强(也即a2a4的值越大);二是η反映高技能生产者相对低技能生产者在两种产品上的优势差异程度,η越大,这种差异越小,极端地η=1,说明高技能生产者相对低技能生产者在两种产品上具有相同的优势;η越小,说明高技能生产者相对低技能生产者在Y产品上优势越弱。利用η与劳动分工的关系,可以检验李嘉图的比较优势理论。
(二)自给自足下的收入及收入不平等
在自给自足下,根据式(1)和式(2),低技能生产者面临的决策问题是

解得 ,因此低技能生产者的效用为:
,因此低技能生产者的效用为:
U1=a1a3=1 (5)
同理,根据式(1)和式(3),高技能生产者的效用为:
U2=a2a4=ηa42 (6)
两行为人的收入不平等如果用效用比来反映,则自给自足下的收入不平等程度D0为式(6)和式(5)之比:
D0=ηa42 (7)
(三)按比较优势分工下的收入及收入平等
由于高技能生产者在产品X的生产上具有优势,一个合意的分工格局是高技能生产者专业生产产品X,低技能生产者专业生产产品Y。为简单起见,不讨论交易成本。设低技能生产者在劳动分工模式下消费Y和X两种产品的份额为α和β,表1列出了两个行为人按比较优势分工下的生产量和消费份额。
下面用纳什议价解来模拟产品的分配①。在这个纳什解中,两个行为人的威胁点是他们在独立自主状态下获得的效用。用U'1和U'2分别表示低技能生产者和高技能生产者在分工下获得的效用,根据纳什合作博弈议价模型[7][8],两人劳动分工的规划可以表示为式(8):
根据一阶条件, ,可得低技能生产者在劳动分工条件下获得的两种产品的份额是相同的,即α=β。将α=β代入一阶条件,可得到式(9):
,可得低技能生产者在劳动分工条件下获得的两种产品的份额是相同的,即α=β。将α=β代入一阶条件,可得到式(9):
命题1:在劳动分工条件下,低技能生产者获得的产品份额(β或α)与高技能生产者的总体优势强度系数η存在负相关关系,收入差距(高技能生产者效用与低技能生产者效用之比)与高技能生产者的总体优势强度系数η存在正相关关系。
证明:对式(9)两端以β为因变量,以η为自应量进行求导,可得到式(10):
由于 ,说明高技能生产者的总体优势强度系数越大,β越小,两变量间存在负相关关系。
,说明高技能生产者的总体优势强度系数越大,β越小,两变量间存在负相关关系。
劳动分工下的收入差距(D1)用高技能生产者效用与低技能生产者效用之比来表示,则:
基于式(11)和式(10),D1关于η的一阶导数为:
由于 ,所以高技能生产的总体优势强度系数越大,在劳动分工条件下两行为人收入差距越大。
,所以高技能生产的总体优势强度系数越大,在劳动分工条件下两行为人收入差距越大。
命题2:高技能生产者的总体优势强度系数η界定了一个分工可行域,只有η处于可行域内,两生产者才能进行有利可图的分工生产。当两生产者之间的总体生产效率差异太大时,进行分工合作的利益基础会逐渐消失,因此李嘉图的比较优势理论是具有约束条件的。
证明:η与β的取值受三个基本条件约束:(1)两行为人进行分工合作生产,在分工下的效用应当不低于各自在自给自足下的效用,也就是U'1≥U1,且U'2≥U2;(2)η与β负相关,β最大时,η最小;(3)由于高技能生产者的强势,在分工条件下低技能生产者获得的产品份额不可能超过高技能生产者所得份额,即β≤0.5。根据这三个条件,结合式(9),可以得到满足分工的η和β的取值范围:
其中β主要由η决定,所以η的取值范围定义了分工的可行域。这一分工的可行域表明,只有比较优势处于一定的范围才能够导致共赢的分工生产。因此李嘉图的比较优势理论是具有约束条件的③。李嘉图的比较优势理论认为,在两生产者、两产品的情况下,如果第一个人生产产品Y和X的生产率都绝对地低于第二个人,但只要这两个人在生产产品Y上的生产率的比率大于产品X,则第一个人在生产产品X上就有一种比较优势,因为她在生产上的绝对劣势要小于Y生产上的劣势。李嘉图认为,只要存在着这种比较优势,则即使一个国家在任何产品的生产上都没有绝对优势,它也能像其他在所有产品生产上都具有绝对优势的国家一样从贸易中得到好处。结合此处的模型环境,李嘉图比较优势理论要求的分工生产条件就是0<η<1。显然,式(13)表明,李嘉图给出的条件过于宽泛,在0<η<1的区域中,有部分η取值会导致无效分工,不会产生共赢的分工生产格局。在 的区间,β>0.5,是不可能区域,由于违背了高技能生产者的假定,不予讨论。在
的区间,β>0.5,是不可能区域,由于违背了高技能生产者的假定,不予讨论。在 的区间,高技能生产者所有产品的生产效率都非常高,此时有U'2<U1,U'1<U2,也就是高技能生产者和低技能生产者在分工下的效用反而低于两者自给自足下的效用,因此是无效的劳动分工,自给自足是理性选择。
的区间,高技能生产者所有产品的生产效率都非常高,此时有U'2<U1,U'1<U2,也就是高技能生产者和低技能生产者在分工下的效用反而低于两者自给自足下的效用,因此是无效的劳动分工,自给自足是理性选择。
命题3:在可行域上,高技能生产者的总体优势强度系数η取端点上的最大值或最小值时,分工下的收入差距刚好等于自给自足下的收入差距;当η不取端点值时,分工下的收入差距小于自给自足下的收入差距。因此,劳动分工具有缩小收入差距的效应。
证明:取最小值, ,β=0.5,劳动分工下的收入差距
,β=0.5,劳动分工下的收入差距 ,自给自足下的收入差距D0=ηa42=1;所以D1=D0。当
,自给自足下的收入差距D0=ηa42=1;所以D1=D0。当 ,D1=D0=ηa42。高技能生产者的总体优势强度系数η取端点上的最大值或最小值时,分工下的收入差距刚好等于自给自足下的收入差距。
,D1=D0=ηa42。高技能生产者的总体优势强度系数η取端点上的最大值或最小值时,分工下的收入差距刚好等于自给自足下的收入差距。
自给自足下的收入差距D0=ηa42,D0与η是一条直线关系,其斜率为a42。由于直线D0和曲线D1在η的两个端点上相交,因此欲证明“η不取端点值时,分工下的收入差距小于自给自足下的收入差距”的命题,只需要证明D1在η的定义域中是严格凸的,D1曲线在直线D0之下,则分工下的收入差距D1小于自给自足下的收入差距D0。对于二阶可微函数而言,严格凸的含义就是要求D1对于η的二阶导数大于零。
 (14)
(14)
其中Φ(.)=-4β2a4×Γ(.)-1,Γ(.)=(12β2-22β+9),由于 是关于β单调递减的,Γ(.)在β=0.5处取得最小值,Γ(0.5)=1,所以Γ(.)>0,则Φ(.)<0;由于
是关于β单调递减的,Γ(.)在β=0.5处取得最小值,Γ(0.5)=1,所以Γ(.)>0,则Φ(.)<0;由于 ,所以D1对于η的二阶导数
,所以D1对于η的二阶导数 ,由此证明分工下的收入差距D1是严格凸的。当η在分工可行域内部取值时,分工下的收入差距小于自给自足下的收入差距,劳动分工具有缩小收入差距的效应。
,由此证明分工下的收入差距D1是严格凸的。当η在分工可行域内部取值时,分工下的收入差距小于自给自足下的收入差距,劳动分工具有缩小收入差距的效应。
二、劳动分工与收入不平等关系:运用Matlab的数值模拟
下面借助于Matlab,对命题1、命题2和命题3进行数值模拟,以便更直观地认识劳动分工与收入不平等关系。
(一)命题1的数值模拟
取a4为2、3、4、5四种情况,根据式(9),利用Matlab的隐函数绘图功能,可以绘制出低技能生产者获得的产品份额β与η的关系(见图一,下页)。图一的左图显示,随着η的增大,β处于递减的状态;同时随着a4的增大,β也相应缩小;η与a4同时增大时,β减少的速度更快。因此低技能生产者获得的分工利益与高技能生产者的总体优势强度呈负相关。
根据式(11)可以解得 ,将β的这一解析式代入式(9),可以得到D1关于η的隐函数,利用Matlab的隐函数绘图功能,可以绘制出分工下的收入差距与η的关系(见图一)。图一的右图显示,η越大,收入差距越大;同时a4越大,收入差距越大。η与a4同时增大时,收入差距增长更加迅速。
,将β的这一解析式代入式(9),可以得到D1关于η的隐函数,利用Matlab的隐函数绘图功能,可以绘制出分工下的收入差距与η的关系(见图一)。图一的右图显示,η越大,收入差距越大;同时a4越大,收入差距越大。η与a4同时增大时,收入差距增长更加迅速。
(二)命题2和命题3的数据模拟
根据式(13),可以计算出不同a4取值下η的分工可行的取值范围(见表2)。当a4为2时,η的取值范围为0.25~0.84;a4为5时,η的取值范围缩减至0.04~0.48,因此当a4取值越小,η的最大值和最小值越大;反之,η的最大值和最小值越小。另外,当a4为2时,η可行域距(η的最大值与最小值之差)为0.59,而a4为5时,η可行域距缩减至0.44,因此a4取值越小,η可行域距越大,两生产者分工合作的空间就越大。a4取值越大,η可行域距越小,两生产者进行分工合作的空间就越小。
图一 η与β、收入差距D1的关系
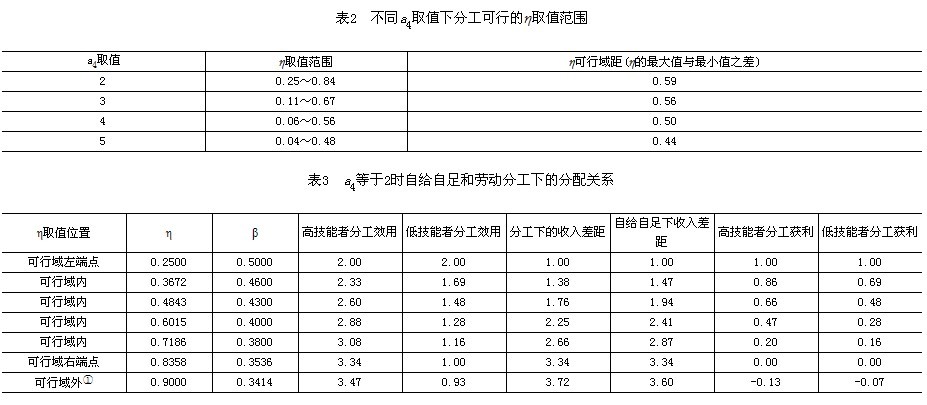
注:①在可行域外,高技能者在自给自足下的效用为ηa42;当η=0.9000,a4=2时,高技能者在自给自足下的效用为3.60,而分工下的效用只有3.47,因此产生分工的负效应。
