M个供应商、1个制造商和N个经销商的三级供应链竞合博弈协调模型

内容提要：本文以供应链系统利润最大化和节点企业利润最大化为目标，建立了M个供应商、1个制造商和N个经销商的三级供应链的竞争合作博弈协调模型。发现核心企业通过制定适当的采购策略、采购价格、研发补贴率、批发策略、批发价格、促销补贴率，可以协调供应链上各节点企业的利益；最后通过算例仿真验证了模型的有效性。
    关键词：三级供应链 博弈 协调模型
    作者简介：郭红莲，北京物资学院商学院讲师，中国农业大学经济管理学院博士研究生；侯云先，中国农业大学经济管理学院。（北京 100083）；杨宝宏，北京物资学院商学院。（北京 101149）
    1引言
    随着经济全球化、一体化和信息化进程的深入，企业之间的竞争已经转变成了供应链之间的竞争，供应链的协调是目前学术界的一个热点和难点。从上世纪80年代起，中外学者就对于这个问题作了大量的相关研究。关于供应链效率方面，Tirole(1988)指出，由于供应链节点企业之间存在相互竞争，他们之间的交易价格会扭曲供应链上的相对成本结构，造成了供应链的低效率，因此在分散决策情况下很难实现供应链整体利润的优化[1]。Cachon和Lariviere(1999)研究了生产能力选择和分配的企业战略行为及其对供应链绩效的影响[2]。Ugarte和Oren(2000)比较了在集中指挥和控制、集中信息纰漏和内部分散信息纰漏三种协调政策下的供应链效率[3]。Tsay和Agrawal(2000)分析了基于价格和服务竞争的供应链动态演变情况[4]。Wang和Gerchak(2001)建立了一个需求决定于货架摆放量的供应链协调模型[5]。包裕玲(2008)分析了不同的年订货量、订货周期、订货次数、单次订购量条件下，多个订货商的两层供应链Stackelberg协调博弈，结果表明通过适当的价格折扣策略，可以改善整个供应链的整体运作[6]。肖条军等(2005)建立了一个基于需求促销和分销管理决策的、包括1个制造商和2个经销商的供应链协调模型[7]。张子健等(2008)考虑了研发不确定条件下的供应商参与协同设计决策，找出了在各种限制因素和相关因素下其最适合的参与程度[8]。
    在激励机制设计方面，Celikbas，Shanthikumar和Swaminathan(1999)讨论了通过市场和制造部门之间的惩罚协议来协调供应链的机制[9]。Corbett和DeCroix(2001)设计了一个供应链上原材料间接供应的利益共享契约模型[10]。丁丁和陈剑(2008)研究了在一个周期内，柔性利润政策下易逝品的三级供应链协调问题[11]。曹细玉等(2006)针对易逝品供应链中的联合广告投入、订货策略与协调问题进行了研究[12]。赵道致、何龙飞(2007)运用downside—risk约束对一个三层供应链模型中风险厌恶型分销商与其下游的风险中性零售商之间的合作进行了契约设计和建模[13]。李善良、朱道立(2005)对不对称信息下供应链线性激励契约委托代理进行了分析[14]。邵晓峰、季建华(2008)研究了基于补偿合约的供应链定价与能力设计的协调问题，分析比较了在集成供应链与独立决策的供应链中的定价与能力计划策略，提出了一种能够有效协调制造商和供应商的决策行为的补偿合约[15]。Tsay(1999)研究了利用数量柔性合约来对供应商进行激励[16]。Taylor(2002)则研究了运用渠道折扣来解决有销售努力效应的供应链协调问题[17]。
    上述文献研究的大都是两级供应链系统[2-10，14-17]，对三级供应链系统的研究也仅限于1个供应商、1个制造商和1个经销商组成的系统[11-13]，而实际中，大多数企业拥有多个供应商和经销商，如上海通用汽车就有3500多个供应商、近600个经销商；深圳民润超市拥有500多个供应商。其次，对于供应链的协调，目标是优化生产能力[2]、库存量[6，11，12]，手段是价格折扣[6，17]、惩罚约束[9，15]机制。本文在以上学者的研究基础之上，主要关注拥有M个供应商、1个制造商和N个经销商的三级供应链系统，以供应链利润最大化为协调目标，并假设供应链利润的优化来源于市场需求的增加和生产成本的降低。为了增加销售，经销商一般会为广告等促销手段作出投资；为了降低生产成本，供应商一般会作出研发投资。我们的模型旨在研究核心企业能否通过适当的政策、价格、补贴率等激励措施来诱导供应商、经销商分别作出系统最优的研发投资和促销投资来最大化整个供应链系统的利润，同时优化各个节点企业的利润。
    2集中决策
    集中决策下的供应链系统，类似由1个供应商、1个制造商(核心企业)和1个经销商组成的三级供应链系统。首先，我们借鉴Wang和Gerchak(2001)的模型，一般的，需求随着促销投资的增加而增加，但投资的边际需求递减，所以假设消费者总需求函数为：
    
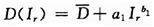
    其中：
    
    
    
    定理1得证。
    3分散决策
    
    由于投资一方面有可能降低产品成本，还可获得研发补贴和更多市场份额，所以理性供应商应该都投资，所以我们只考虑第(1)种情况。供应商的利润函数为共同知识，供应商之间进行完全信息静态投资博弈，每个供应商都选择最大化自己利润的投资，由于存在竞争，设他们的保留效用是利润为
    
    
    定理2表明，N个经销商的促销投资一定是相等的，类似于国家之间的军备竞赛，因为只要有一个经销商比其他经销商多投资，他就会占有更多的市场份额，由于所有的经销商都不甘落后，一定都会尽力赶超先多投资的经销商，所以最终的结果一定是所有的经销商投资相同的数额；同时表明所有经销商的投资之和是一定值时会使供应商利润之和最大化，因为如果系统投资小于该值，则会将市场份额的一部分拱手让与供应链系统的竞争对手(或替代品厂家)，如果系统投资大于该值，则会由于市场饱和而进行无谓的投资，造成资源浪费，得不偿失。由于是完全信息静态博弈，理性的经销商选择系统最优投资的1/N来“瓜分”市场，这样既不造成整个供应链系统资源浪费、数败俱伤和市场份额的丢失，又能在竞争中各得其所，达成均衡。
    定理3制造商——经销商之间的协调：能够满足
    ：
    
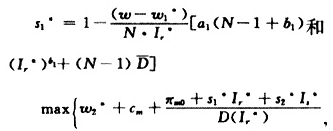    定理3表明，当批发价格很高时，为了避免损伤经销商积极性，核心企业应给予一个很高的促销补贴率来激励经销商；当批发价格很低时，为了保护自身利益，核心企业应适当降低促销补贴率。随着N的增大，经销商间的竞争会更加激烈，使批发价的最小值增大而最大值减小，缩小了可协调的批发价格范围，也就削弱了经销商的讨价还价能力，每个经销商的利润呈指数规律递减。
    
    定理4表明，为了获得制造商的更多订货和不断降低成本，供应商之间会展开研发投资角逐，同样类似于军备竞赛，结果是各个供应商的投资相等；同时表明，该供应链系统的研发投资之和为一定值时，供应商利润之和最大化，如果研发投资小于该定值，则降低成本仍有潜力可挖，如果研发投资大于该定值，则由于成本已达到最低极限，会造成资源浪费。又由于是完全信息静态博弈，每个供应商会各自选择系统最优投资的1/M来分割制造商需求。
    定理5供应商——制造商的协调：当制造商——经销商供应链协调时，能够满足
    
    定理5表明，当采购价格很低时，制造商为了保护供应商的研发积极性，应提供一个较大的研发补贴率；当采购价格很高时，制造商为了自身利益，应提供一个较低的研发补贴率。研发降低了供应商的生产成本，供应商可接受的采购价格下限降低，增强了自己承受低价格的耐力，增大了自己的利润空间，这也显示了企业研发创新和低成本带来的竞争优势。随着M的增大，供应商竞争日趋激烈，采购价格的最大值会降低；由于协调变得越来越困难，因此制造商为了实施激励，采购价格的最小值会上升，当M达到一定值时，采购价格会收敛于某一点。
    经过协调后供应链上各节点企业的利润为：
    
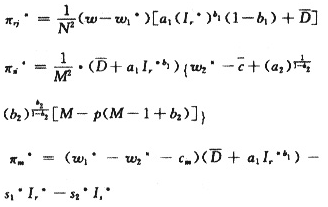
    4算例仿真
    某手机厂生产某一型号的手机，向供应商采购的原料价格为360元/部，制造成本为500元/部，预计初始市场需求为100000部，售价1000元/部。经验表明市场需求与促销投资关系为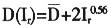，原材料成本与研发投资的关系为
    
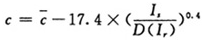
    供应商认为研发成功的概率p＝0.8。表1表明了假设初始时期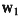＝955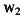，＝405的供应商系统、经销商系统做最优投资与不投资时的供应链系统利润比较。
    
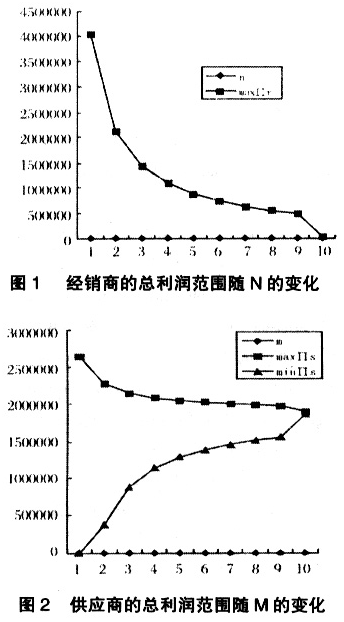
    在模拟计算M个供应商、1个制造商、N个经销商(M＞2，N＞2)构成的供应链系统时，我们发现，从M＝1到M＝2、从N＝1到N＝2会发生质的变化。因为在1个供应商、1个制造商、1个经销商构成的供应链系统中，供应商、制造商和经销商的地位平等，所以当制造商和经销商保留效用与制造商的保留效用相当时(如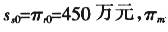＝500万元)，仍能协调。但当M＞2，N＞2时，如果供应商和经销商的保留效用不变，则供应链不能协调。因此，我们假定供应商和经销商的保留效用为0，则我们得到了不同的经销商数量下，供应链被协调时批发价格及促销补贴率的范围(表2)，以及不同的供应商数量下，供应链被协调时采购价格及研发补贴率的范围(表3)。而表4则表示不同的供应商和经销商数量组合下，制造商的利润范围。可以看出，制造商的最大利润与经销商数量无关，而供应商数量越多，制造商的利润最大值越低。图1、图2则分别表达了供应链被协调后，经销商的总利润范围随N的变化趋势和供应商的总利润范围随M的变化趋势(横坐标为10处分别代表N＝100和M＝100时的情形)。
    
    
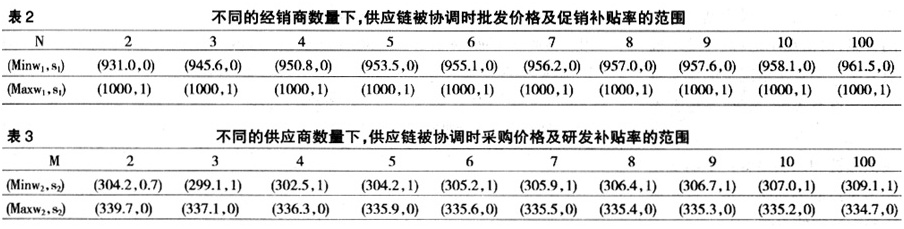
    这与我们实际观察到的结果基本一致，即如果核心企业的规模越大，供应商数量越多，则在谈判中自主定价能力越强，核心企业得到的利润越大。如零售业巨人沃尔玛就经常要求供应商降低其产品价格。但如果超出限度，不能满足供应商的保留利润，则供应商会投向其他零售商，这在沃尔玛就曾发生过，后来沃尔玛意识到了这一点，便又重新与供应商合作，提高了采购价格。而对于宝洁公司这样的大型制造商，与经销商的批发价格一般由宝洁公司确定，即便是沃尔玛也不与其讨价还价。另外模型还可从一个侧面解释中国的“三农”问题：由于农户数量巨大，在供应链中毫无农产品定价话语权，因此农民的收入微乎其微；而如果减少农户数量，农民的增收问题则可在一定程度上得以解决。
    
    5结语
    本文将博弈模型引入供应链的协调过程中，研究发现核心企业通过制定合适的采购政策、采购价格、研发补贴率、批发政策、批发价格以及适当的促销补贴率，可以实现三级供应链的协调，使供应链的整体利润最大化，同时增加供应链上各节点企业的效益，达到共赢的局面。
    本模型旨在追求供应链的高效率，即最大限度地提高市场占有率的同时，使成本达到最小，适合于生命周期中处于成长期至成熟期的产品，这些产品的需求弹性大，促销效果明显，单位产品成本高，降低成本的潜力大；同时适合多个供应商提供的产品是同质、无差异、可互相替代的情形，如汽车、手机、农牧产品等的供应链协调。
    本文的不足之处是模型基于信息完全的背景，对信息不对称、环境不确定等更复杂、更真实情况下的供应链协调问题还没有考虑，另外，本模型不适合以快速响应客户需求为宗旨的敏捷反应供应链和以满足客户不断变化的需要为重点的创新供应链，这些将是以后努力研究的方向。
    参考文献：
    [1]Tirole, J. The Theory of Industrial Organization[M]. Cambridge, MA: The MIT Press, 1988.
    [2]Cachon, G. P. and M. A. Lariviere. Capacity Choice and Allocation: Strategic Behavior and Supply Chain Performance[J]. Management Science, 1999, 45(8):1091—1108.
    [3]Ugarte, A. and S. Oren. Coordination of Internal Supply Chains in Vertically Integrated High-Tech Manufacturing Organizations(HTMOs)[J]. International Journal of Production Economics, 2000, 67: 235—252.
    [4]Tsay, A. and N. Aggrawal. Channel Dynamics under Price and Service Competition[J]. Manufacturing & Service Operations Management, 2000, 2(4):372—391.
    [5]Wang, Y. and Y. Gerchak. Supply Chain Coordination when Demand is Shelf-Space-Dependent[J]. Manufacturing & Service Operations Management, 2001, 3(1):82—87.
    [6]包裕玲.多个订货商的两层供应链Stackelberg协调博弈分析[J].中国管理科学，2008，16(3):68—72.
    [7]TIAOJUN XIAO, GANG YU, ZHAOHAN SHENG, YUSEN XIA. Coordination of a Supply Chain with One-Manufacturer and Two-Retailers Under Demand Promotion and Disruption Management Decisions[J]. Annals of Operations Research, 2005,135: 87—109.
    [8]张子键，刘伟，张婉君.基于不确定条件下的供应商参与协同设计决策分析[J].中国管理科学，2008，16(3)：95—101.
    [9]Celikbas, M., J. G. Shanthikumar, and J. M. Swaminathan. Coordinating Production Quantities and Demand Forecasts through Penalty Schemes[J]. IIE Transactions, 1999,31：851—864.
    [10]Corbett, C. J. and G. A. DeCroix. Shared-Savings Contracts for Indirect Materials in Supply Chains: Channel Profits and Environmental Impacts[J]. Management Science, 2001, 47(7):881—893.
    [11]Ding, Ding, Chen, Jian. Coordinating a three level supply chain with flexible return policies[J]. Omega, 2008, 36(5)：865—876.
    [12]曹细玉，宁宣熙，覃艳华.易逝品供应链中的联合广告投入、订货策略与协调问题研究[J].系统工程理论与实践，2006，3(3)：102—107.
    [13]赵道致，何龙飞.Downside—Risk控制下的供应链合作契约研究[J].系统工程理论与实践，2007，(4)：34—40.
    [14]李善良，朱道立.不对称信息下供应链线性激励契约委托代理分析[J].计算机集成制造系统，2005，11(12)：1758—1762.
    [15]邵晓峰，季建华.基于补偿合约的供应链定价与能力设计的协调问题研究[J].中国管理科学，2008，(8)：62—68.
    [16]Tsay, A. A. The Quantity Flexibility Contract and Supplier-Customer Incentives[J]. Management Science, 1999,45(10)：1339—1358.
    [17]Taylor, T. A. Supply Chain Coordination under Channel Rebates with Sales Effort Effects[J]. Management Science, 2002,48(8)：992—1007.^