内容提要:合作博弈理论中,稳定的财富分配方案是维系大联盟的根本,所以一直是经济学家和管理工作者极感兴趣的焦点之一。本文研究“考虑绩效因素”的合作博弈中的核分配问题,提出“简单化核——占优核——真核——Aubin核”的探索途径。对于具有广泛实用意义的绩效“集团”博弈,本文利用纠正国外同行在他们专著中的致命错误从而证明的“真核”与“占优核”等价的重要结论,为寻求公平合理的分配方案提供了理论基础和实际操作方法。
关键词:绩效“集团”博弈/Aubin核/真核/占优核/简单化核作者简介:施锡铨,电子信箱:xqshi@mail.shufe.edu.cn,上海财经大学金融学院(上海 200433);孙修勇,电子信箱:tdsxy@163.com,通讯作者,上海财经大学金融学院(博士在读),凯里学院(教师)。
一、引言
社会稳定问题是世界各国关心的问题,社会的稳定依赖于社会的公平公正。而社会的公平公正很大程度上取决于社会财富分配的公平合理性。这里,社会财富分配包括了盈利或资源的分配、成本的分摊和经济体之间对某些感兴趣内容的匹配等等。因此,研究分配公平合理性的合作博弈理论引起了世界各国的管理工作者和经济学家的极大兴趣,并且越来越受到经济学界和管理学界的重视。美国经济学家Alvin Roth & Lloyd Shapley凭借“稳定分配理论和市场设计实践”分享了2012年诺贝尔经济学奖是一个最好的例证。在我国,随着深入改革的需要,近几年来也出现了不少关于社会财富分配的研究成果,其中大部分涉及到关于财富分配的公平合理性,如倪迪、符学东(1990)通过对收入分配体制方面重大改革的回顾,提出了对当时社会收入分配不公的认识及其对策;杨圣明、郝梅瑞(Yang & Hao,2007)在他们的文章中分析了贫富两极分化的主观及客观原因,并提出政府必须保证社会公平,既不能越位,更不能缺位的解决方案;有的研究以中国城镇的住房改革为例,从资产转换的角度研究了中国体制转型过程中城镇居民家庭财富积累及分配差距的产生(何晓斌、夏凡,2012)。
合作博弈理论指出,为了维系大联盟(社会)的稳定,分配方案至少必须保证:任何局中人或者部分局中人组成的较小联盟(称为子联盟)如果离开大联盟“自起炉灶”,他们将发现由此所得到的盈利不会超过这个分配方案给予他们的东西,从而使得他们愿意“凝聚”在大联盟中。我们称这样的分配方案使得大联盟具有稳定性,或者说,这个分配方案对于所有的子联盟都是稳定的。显然,稳定的分配方案在相当程度上被认为具有一定的公平合理性。合作博弈理论中最为成熟也广泛被人们认可的“核”分配就是这样的分配方案。“核”分配概念有一个基本的假设:大联盟中所有的局中人都是全力投入合作的,只要大联盟实施一个公平合理的分配方案,大家都愿意凝聚在大联盟中,同心协力做大蛋糕。然而,现实生活并没有那么完美,社会财富分配问题是个复杂的问题,譬如,不是每个局中人都是百分之百地投入大联盟中,具有相同“地位”和相同“能力”的局中人,由于各人的投入程度(或者称“努力程度”)不同,从而不可能对大联盟做出同样的贡献,从公平合理的角度出发,不应该分配给他们相同的盈利,这就是时下所关心的“考虑绩效因素”的分配方案,简单地说,即使是相同“级别”或“职称”的局中人,鉴于他们的“投入”不同,从而引起“绩效”的不同,公平合理的分配方案应该给予他们不同的盈利分配。对于这样的情况,有必要另外建立有关博弈模型,不妨称这样的博弈为绩效博弈。
本文的第二部分把绩效博弈与合作博弈理论研究中正在兴起的模糊博弈(Aubin,1974)相联系,对于这类模型,我们也将关心它的“核”分配——对于所有的子联盟都具有稳定性的分配方案,不过,这里的子联盟必须包含所有“考虑绩效因素”的子联盟。为了说明“考虑绩效因素”的子联盟的含义,举一个最简单的例子:譬如局中人1与局中人2组成一个原先意义下的两人联盟{1,2},假设他们各自的投入水平分别是
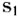 和
和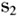 ,其中
,其中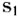 和
和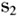 是位于0与1之间的数,这两个数在某种程度上可以看作是他们相应的绩效水平,于是,{
是位于0与1之间的数,这两个数在某种程度上可以看作是他们相应的绩效水平,于是,{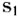 ,
,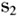 ,0,…,0}就是考虑到他们两个绩效因素的子联盟(其他人不参加这个联盟,因此,在这个联盟中与这些人相应的绩效水平都为0)。对于所有“考虑绩效因素”的子联盟具有稳定性的分配的集合在合作博弈理论中称为“Aubin核”(Aubin,1981),这里简称为“核”。“核”分配的稳定性自然受到人们的欢迎,至少给人一个思路,一个比较令人满意的分配方案应该从核分配中挑选。然而,想设计一个“核”分配方案或者想验证一个方案是否属于“核”,是相当不容易的事情。因为这需要顾及到无限多个“考虑绩效因素”的子联盟是否对方案“满意”或者至少没有反对意见,因此,想完全地得到“核”再从其中去挑选“佼佼者”又谈何容易。甚至,有时候“核”分配有可能不存在,根本无从找起。有关学者对付这个难题的办法是适当放宽稳定性的要求或者缩小稳定的范围,由此逐步提出“真核”(Tijs et al.,2004)、“占优核”(Branzei et al.,2008)等等概念,用意很清楚,总是先求稳定性比较强的,如果找不到或者甚至不存在,那么只得退而求次之,如此下去。这些概念和有关讨论将在本文的第二部分介绍。
,0,…,0}就是考虑到他们两个绩效因素的子联盟(其他人不参加这个联盟,因此,在这个联盟中与这些人相应的绩效水平都为0)。对于所有“考虑绩效因素”的子联盟具有稳定性的分配的集合在合作博弈理论中称为“Aubin核”(Aubin,1981),这里简称为“核”。“核”分配的稳定性自然受到人们的欢迎,至少给人一个思路,一个比较令人满意的分配方案应该从核分配中挑选。然而,想设计一个“核”分配方案或者想验证一个方案是否属于“核”,是相当不容易的事情。因为这需要顾及到无限多个“考虑绩效因素”的子联盟是否对方案“满意”或者至少没有反对意见,因此,想完全地得到“核”再从其中去挑选“佼佼者”又谈何容易。甚至,有时候“核”分配有可能不存在,根本无从找起。有关学者对付这个难题的办法是适当放宽稳定性的要求或者缩小稳定的范围,由此逐步提出“真核”(Tijs et al.,2004)、“占优核”(Branzei et al.,2008)等等概念,用意很清楚,总是先求稳定性比较强的,如果找不到或者甚至不存在,那么只得退而求次之,如此下去。这些概念和有关讨论将在本文的第二部分介绍。应该承认,上述思路是符合科学逻辑的。而且对于一般的绩效博弈,由于上述几类“核”成立(或者在某种程度上成立)从大到小的包含关系,先求“核”,不行再退而求“真核”,这样形成从小到大寻求尽可能好的解的途径,是人人都能接受的想法。但是,在实际操作中,大联盟的管理者(诸如政府决策者、公司高层等)很难沿着这种思路去设计分配方案以保证公正。根据各种类型“核”的定义及其性质,在本文的第三部分,我们建议,方案的设计应该逆向操作,遵循“简单化核”——“占优核”——“真核”——“核”的思路,一步一步走下去,尽可能地“精益求精”,只有这样,才能真正达到维系大联盟的目的。
倘若存在一类特殊的有实际意义的绩效博弈发生了两类核等价的现象,无疑使我们在处理此类博弈时大大提高了工作效率,可以比较容易地确定合意的分配方案。我们最近成功证明的一个有关合作博弈的数学结果(施锡铨,2012)在这方面有令人满意的应用效果。
在现实经济生活中有这样的一类合作博弈,其中的部分局中人拥有否决权,而另外的大部分局中人则没有否决权,譬如,著名的大老板博弈(Muto et al.,1988),其中大老板(譬如工厂主、农场主等等)拥有否决权而所有的雇工完全没有否决权。现在的许多公司就存在这种现象,不过,在那里拥有否决权的董事会成员不止一个。此类模型在合作博弈中被称为“集团”(clan)博弈(Potters et al.,1989),需要注意的是,这里的“集团”只是那些拥有否决权的局中人集合的称呼,并不表示他们形成了一个“一致对外的团体”。在许多“集团”博弈中,可以假设“集团”成员是百分之百投入合作的(因为他们是“老板”,他们总是希望公司的“蛋糕”越大越好),但是非“集团”成员则未必如此。不妨暂且称这样的博弈为绩效“集团”博弈。在著作“Models in Cooperative Game Theory”(Branzei et al.,2008)中,作者认为,绩效“集团”博弈(Tijs et al.,2004)的“占优核”等价于“真核”。如果这个结论成立,在绩效“集团”博弈中,沿着我们提供的思路,由于“占优核”一定为非空,可以轻而易举地确定比较理想方案的范围,然后再做下一步细致的工作。可惜的是,他们在证明中把复杂的“考虑绩效因素”的合作博弈当作一般的合作博弈来处理,这样去证明显然无法说明结论的正确性。本文作者曾经向他们指出,他们在专著中存在的问题并得到了他们的认可,甚至还向我们询问有无正确的答案。我们得到的数学结果启发了在考虑绩效因素的社会财富分配中采用逆向求解的想法。但是由于其证明过程的纯数学味极强,在本文的第四部分我们只能阐述为何他们是错误的和我们如何纠正的基本思路,重点解释我们所加条件的意义并讨论绩效“集团”博弈的财富分配方案制定时如何应用第三部分所提出的建议。
熟知合作博弈理论的人也许会争辩,有些博弈的核已经在理论上具有明确的形式,为什么还要去探索呢?这个问题的回答很简单,理论上正确的东西未必可以实际操作。例如,如果博弈是凸的话,上面提到的核有可能全部等价。然而在应用中凸博弈(Tijs & Branzei,2004)的验证需要用到博弈的特征函数,而事实上在许多场合这件事情本身很难确定,借用统计学的一个术语,我们处理的常常是“非参数”问题。有关这个问题在本文的第三和第四部分将进一步讨论。
二、有关绩效博弈模型的建立和它的各类解
(一)不考虑绩效因素的合作博弈

这里显然只考虑了局中人的能力而根本不涉及他们的绩效如何。一个高级工拿着较高的薪水却出力甚少,这就缺乏了公平合理性,会造成大联盟“凝聚力”的涣散。在制定财富分配方案的过程中,除了考虑个人的能力以外,添加绩效因素看来是社会稳定的必然要求。
(二)绩效博弈及其核
如何将绩效因素量化不是一件容易的事情,譬如,两个教师具有相同的职称,有着相同的年龄和学历,如果在同一学年内,一个人发表了一篇论文,另一个人没有论文,武断地说前者比后者绩效好,似乎并不很妥当。对绩效的不同界定会引起不同的分配方案。本文中,我们以局中人对合作的投入程度(或对工作的努力程度)作为衡量“绩效”的依据。因为我们认为,同等地位同等能力的人,只要有同等的投入,理应有几乎相同的绩效。当然,“投入”或“努力”本身也存在界定问题,但是它的界定稍微方便一些,一则是因为人们对努力不努力常常有公认,二来是多数情况中绩效存在一个“时效”问题。

近代合作博弈理论研究中有些学者称这些联盟为“模糊”(fuzzy)联盟,其用意是指局中人对合作的投入是模糊且不确定的。我们认为绩效并非完全处于模糊状态,况且“模糊”两字容易使人联想到模糊数学问题,而这两者不是一回事情!因此这里还是称它们为绩效联盟。相应的绩效博弈中的特征函数v(s)自然是绩效联盟的函数。
绩效博弈的核与不考虑绩效的合作博弈的核一样,需要满足一些条件,有效性与个人理性是永恒的(符合这两个条件的分配方案的全体组成了博弈的“配置集”,用I(v)表示),只不过在集体理性的条件中,绩效博弈要求方案对所有的绩效联盟都是稳定的。就是说,对于x(I(v),如果x∈C(v)(这里用C(v)表示核),则对任何绩效联盟s,成立
 。一般子联盟S仅仅是特殊的绩效联盟(其中局中人的绩效要么是百分之百,要么是0),因此,只要考虑绩效问题,一个稳定的解会要求更多的联盟具有稳定性,就凭这一点可知,绩效博弈的核必定包含在一般合作博弈的核内。正因为如此,在制定分配方案时只要把绩效因素考虑进去,往往较难将工作开展下去,这不单单归因于绩效比较难界定,即使绩效容易分辨,还是很难找到若干使得所有(无限个)绩效联盟都难以拒绝的分配方案。倘若我们推出一个方案,先不说所有(无限个)绩效联盟如何评价它,假如有一个局中人看到这个方案后,他盘算着自己应该付出多少努力才对自己最有利,如果他觉得他不必百分之百地投入,那么,这个方案多少不尽如人意。要知道,合作博弈理论之所以研究模糊博弈,其宗旨是设计合理的制度以激励所有的局中人“心甘情愿”地全力投入大联盟的合作中去,或者说,旨在提高大联盟的凝聚力。同样,研究考虑绩效因素的社会财富分配问题,其目的并非主要是“奖励绩效高的,惩罚绩效差的”,制定考虑绩效因素的分配方案,其最终目的是鼓励所有人凝聚在大联盟中,只有这样的方案是稳定的,它能维系大联盟(社会、公司等等)的稳定,这个观点在本文下面的讨论中显得非常重要!
。一般子联盟S仅仅是特殊的绩效联盟(其中局中人的绩效要么是百分之百,要么是0),因此,只要考虑绩效问题,一个稳定的解会要求更多的联盟具有稳定性,就凭这一点可知,绩效博弈的核必定包含在一般合作博弈的核内。正因为如此,在制定分配方案时只要把绩效因素考虑进去,往往较难将工作开展下去,这不单单归因于绩效比较难界定,即使绩效容易分辨,还是很难找到若干使得所有(无限个)绩效联盟都难以拒绝的分配方案。倘若我们推出一个方案,先不说所有(无限个)绩效联盟如何评价它,假如有一个局中人看到这个方案后,他盘算着自己应该付出多少努力才对自己最有利,如果他觉得他不必百分之百地投入,那么,这个方案多少不尽如人意。要知道,合作博弈理论之所以研究模糊博弈,其宗旨是设计合理的制度以激励所有的局中人“心甘情愿”地全力投入大联盟的合作中去,或者说,旨在提高大联盟的凝聚力。同样,研究考虑绩效因素的社会财富分配问题,其目的并非主要是“奖励绩效高的,惩罚绩效差的”,制定考虑绩效因素的分配方案,其最终目的是鼓励所有人凝聚在大联盟中,只有这样的方案是稳定的,它能维系大联盟(社会、公司等等)的稳定,这个观点在本文下面的讨论中显得非常重要!绩效博弈的困难在于要“照顾”的子联盟比起不考虑绩效因素时大大地增加了范围,引起了“核”的缩小并增加了求解核分配的难度。从科学研究的角度,想解决这样的矛盾最好的办法是减少“照顾对象”,或者说,降低稳定性的要求,根据这种思路,合作博弈理论陆续推出“真核”、“占优核”等有关“解”的概念。
(三)“真核”、“占优核”以及“简单化核”

对于“真核”定义的解释是:任何一个“真子绩效联盟”中的局中人从大联盟中得到盈利的“加权和”(“权”为局中人的绩效水平)大于或等于该“真子绩效联盟”自身生产的总价值。使得“真子绩效联盟”愿意留在大联盟内,至少对大联盟没有反感。表示“真核”
 对于所有的“真子绩效联盟”都是稳定的。但是,对于那些非“真子绩效联盟”(这类联盟的载体包含了大联盟中所有的成员,他们每个人或多或少有点绩效),则不能保证它们“稳定”在大联盟中,因为可能存在一些这样的非“真子绩效联盟”,他们从分配方案中得到的收入总和还不及他们自己生产的总价值,高“能”低“薪”会使他们对方案不满意,从而影响到大联盟的合作。这一点,恰好体现出“真核”与“核”的差异,“核”分配不会生成任何高“能”低“薪”的现象,因此,“核”比“真核”更具稳定性,自然,“核”被“真核”包含。将“核”这个概念延拓到“真核”,常常是在无法找到“核”的情况下,我们不得不退而求稳定性稍微“差”一些“真核”,况且“真核”的验证条件毕竟比“核”要少了许多。然而,明白人很快知道,这种所谓的“方便”不是实质性的。因为验证一个配置是否属于“真核”,同样地使人觉得很难。不过,由于非“真子绩效联盟”的特殊性,如果一个方案是真核成员,那么它是否核元素还是比较容易核实的。这说明,核与真核之间虽然有差异,但毕竟“相差甚微”。
对于所有的“真子绩效联盟”都是稳定的。但是,对于那些非“真子绩效联盟”(这类联盟的载体包含了大联盟中所有的成员,他们每个人或多或少有点绩效),则不能保证它们“稳定”在大联盟中,因为可能存在一些这样的非“真子绩效联盟”,他们从分配方案中得到的收入总和还不及他们自己生产的总价值,高“能”低“薪”会使他们对方案不满意,从而影响到大联盟的合作。这一点,恰好体现出“真核”与“核”的差异,“核”分配不会生成任何高“能”低“薪”的现象,因此,“核”比“真核”更具稳定性,自然,“核”被“真核”包含。将“核”这个概念延拓到“真核”,常常是在无法找到“核”的情况下,我们不得不退而求稳定性稍微“差”一些“真核”,况且“真核”的验证条件毕竟比“核”要少了许多。然而,明白人很快知道,这种所谓的“方便”不是实质性的。因为验证一个配置是否属于“真核”,同样地使人觉得很难。不过,由于非“真子绩效联盟”的特殊性,如果一个方案是真核成员,那么它是否核元素还是比较容易核实的。这说明,核与真核之间虽然有差异,但毕竟“相差甚微”。在现实生活中,人们(尤其是管理者)习惯的逻辑思维方式之一是,一个考虑中的方案,如果找不到一个其他的方案使得“方方面面”都觉得比它更好,那么,这个方案至少不算太差。通俗一点说,你拿不出一个让大家都认为能使自己处境更好的办法来,或者说,你应该拿出一个对自己有利但至少不会“侵害”他人利益的方案,倘若做不到,那么就按照原来提出的办法去做。遵循这种思路,导出一个范围更广的具有一定稳定性的配置集的概念——“占优核”。在介绍“占优核”概念时,首先要搞清楚什么叫“占优”。


最后介绍“简单化核”。这看上去似乎是个“吃大锅饭”的办法,但是,在下面一节中将提出在制定公平合理的分配方案过程中它的重要性。这个办法,其实质是“将复杂的问题简单化”,就是说,只要你出力了,不管你的绩效是达到百分之百,还是仅仅百分之一,都算你可以拿到绩效百分之百的待遇。此时在“新”的博弈中已经没有了绩效联盟,而是原先一般的子联盟
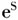 。原来的博弈v经过这样简单化处理以后得到的新博弈记作cr(v)。定义为:
。原来的博弈v经过这样简单化处理以后得到的新博弈记作cr(v)。定义为:
三、“简单化核——占优核——真核——核”
在第二部分,得到了绩效博弈“解概念”的两个关系式(5)和(7),按照合作博弈理论,我们总是希望在核内寻找一个比较理想的方案,它至少在相当程度上具有稳定性。如果核不存在,或者由于绩效联盟太多而困难甚多,就只能退而去求稳定性比较差的“真核”,甚至更差的“占优核”。至于“简单化核”,那是摆不上桌面的方案,因为在市场经济时代,它有“吃大锅饭”之嫌。
我们认为,作为管理者来说,不可能完全沿着理论的研究思路进行操作,相反地,有时候应该运用逆向思维的方式制定方针策略。例如,在制定公平合理的分配方案时,不妨先考虑“占优核”或者“简单化核”形式的方案。“占优核”的想法会得到大家的赞同,因为“占优核”毕竟符合人们日常生活的逻辑思维,同时,合作博弈的理论告诉我们,“占优核”比起“真核”或“核”有个更大的好处,那就是“占优核”是非空的,而“真核”或“核”未必如此,从比较容易着手的且为大多数人容易接受的和一定存在的分配出发,然后再向更稳定的方案探索,这就是“占优核”——“真核”——“核”途径,应该是条比较稳妥的途径。可是,在实际操作中,要找一个没有一个人或没有一个子群反对的方案也不是一件容易的事情。最简单方便的办法就是“简单化核”形式的方案,这是一个市场经济最反感的分配方式。其实拒绝“简单化核”是片面的观点,从人类进步的角度,合作博弈也好,绩效博弈也好,最终目的是鼓励所有的局中人全心全意地投入大联盟的合作中去,如果这个目的达到,那么制定的“简单化核”分配就是最终方案,可以这样说,一个科学的公平合理的最终分配方案实际上是向所有的局中人展现了合作的美好前景。在实际生活中,许多管理者的做法就是符合这个思路的:人们常常拿出一个不考虑绩效的分配方案,然后在执行的过程中围绕着绩效的问题“修修补补”,提出一些条款以奖励那些绩效高的,“惩罚”那些绩效差的。这种做法有点接近于“简单化核”——“真核”——“核”的途径。之所以讲“有点接近”,是因为途径本身需要从众多的“简单化核”元素中去寻找“真核”元素乃至核元素,而不仅仅是做些“修修补补”的工作。
最好的途径是从“简单化核”元素中去确定“占优核”(这一步比较容易操作,总比直接去找“占优核”容易),再往下去寻找“真核”元素乃至核元素,即所谓的“简单化核”——“占优核”——“真核”——“核”的途径。但是,要建立这条途径,必须要搞清楚“简单化核”是否包含“占优核”,并不是所有的绩效博弈都满足这种包含关系,我们在第四部分将介绍的一类具有现实意义的绩效“集团”博弈拥有这个性质,而且,绩效“集团”博弈还拥有更进一步的良好性质,使得在制定此类博弈的分配方案时非常方便。
在介绍绩效“集团”博弈的有关结论前,必须指出,有一类特殊的绩效博弈,特殊到这几种核达到全部等价,那就是凸(模糊)博弈。这个特点使得凸博弈存在唯一的稳定集——占优核。对于这类博弈,所有讨论似乎都显得缺乏意义。其实不然,要验证一个博弈是否凸的,应该验证两个条件:超模性和坐标凸性。这需要从博弈的特征函数着手,并且对所有的绩效子联盟和所有的局中人验证相应的不等式。首先,在处理的社会财富分配问题中,虽然可以知道不少有关问题的知识,但是想知道博弈的特征函数却是几乎不可能的,理论上构造一个凸博弈不成问题,譬如“模糊一致同意博弈”(Branzei et al.,2003),而在实际生活中去确定博弈的特征函数很可能是毫无办法;其次,即使知道了特征函数,要去验证几乎无穷多个不等式也是不可能的。研究凸(模糊)博弈在理论上的确很重要,但指望它在实际中立即可以应用,那么空想的成分似乎多了一些。
四、绩效“集团”博弈及其分配方案的制定

那么,称v为绩效“集团”博弈。
请注意,这里向量的比较大小,是对每个分量进行比较的,即如果对每个i,都有
 成立,我们说s>t(对于不严格的不等式依此类推)。
成立,我们说s>t(对于不严格的不等式依此类推)。绩效“集团”博弈的定义中最为关键的要求是“集团”的否决权,也是该博弈的最与众不同的特点,少了任何一个“集团”成员,任何形式的子联盟都将一事无成;博弈要求的单调性则是一个符合现实的要求,较大的联盟比起较小联盟来总是绩效大一些;第(Ⅲ)个要求也涉及到博弈的特征函数,如果要去验证同样会遇到困难。但是,仔细研究这个条件,可以发现离开了特征函数它仍然可以验证,注意条件
 意味着
意味着 ,即非宗派成员从模糊联盟s中减少了自己的参与水平(从
,即非宗派成员从模糊联盟s中减少了自己的参与水平(从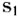 减少到
减少到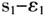 ),这样一来引起了联盟效用的减少,我们定义
),这样一来引起了联盟效用的减少,我们定义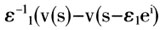 )为由这样的变化所引起的平均边际回报。DAMR性质是指,在包含了全部宗派成员的模糊联盟中,一个非宗派成员在更大一些的模糊联盟t中减少自己的参与水平比起在原来的模糊联盟s中减少自己的参与水平(但是经此变化后的模糊联盟
)为由这样的变化所引起的平均边际回报。DAMR性质是指,在包含了全部宗派成员的模糊联盟中,一个非宗派成员在更大一些的模糊联盟t中减少自己的参与水平比起在原来的模糊联盟s中减少自己的参与水平(但是经此变化后的模糊联盟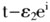 仍然不比变化后的模糊联盟
仍然不比变化后的模糊联盟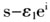 小)引起了平均边际回报的减少。这表明,随着模糊宗派联盟的“扩大”,非宗派成员对于联盟的平均边际效用逐渐减少。这个条件是符合日常生活规律的,而且对博弈的这种感觉并不需要借助于特征函数就可以得到的。
小)引起了平均边际回报的减少。这表明,随着模糊宗派联盟的“扩大”,非宗派成员对于联盟的平均边际效用逐渐减少。这个条件是符合日常生活规律的,而且对博弈的这种感觉并不需要借助于特征函数就可以得到的。根据以上分析,由于后两个条件比较自然,因此在现实中只要存在“集团”,大部分情况可以用绩效“集团”博弈描述。因此我们认为对绩效“集团”博弈的分配进行研究具有比较现实的意义。
绩效“集团”博弈的“简单化核”包含“占优核”,并且在相当自然的条件下“占优核”与“真核”是等价的。由于后者是我们独立证明的,因此我们用定理的形式进行叙述:
定理:设v是绩效“集团”博弈,成立

这个定理的第①部分,其实只要看
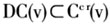 是否成立。对绩效“集团”博弈“简单化”后得到的博弈cr(v)是一个不考虑绩效因素的“集团”博弈,对于这样的博弈,容易知道,其“核”与“占优核”是一致的,又有不考虑绩效因素的“集团”博弈的“占优核”显然应该包含考虑绩效因素的“集团”博弈的“占优核”,这两者一起说明了必定有
是否成立。对绩效“集团”博弈“简单化”后得到的博弈cr(v)是一个不考虑绩效因素的“集团”博弈,对于这样的博弈,容易知道,其“核”与“占优核”是一致的,又有不考虑绩效因素的“集团”博弈的“占优核”显然应该包含考虑绩效因素的“集团”博弈的“占优核”,这两者一起说明了必定有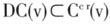 成立。
成立。定理的第②部分,是《Models in Cooperative Game Theory》一书在没有我们所加条件下的“猜测”,之所以说它是“猜测”,是因为书中有关它的证明是错误的。他们的证明只能说明在不考虑绩效因素的“集团”博弈中结论是成立的,而这一点在我们的定理第①部分中已知是显然的事实。一旦考虑绩效因素,他们所用的不等式显而易见是不成立的。我们利用了

这个结论指出了绩效“集团”博弈中的“占优核”等价于“真核”,使得“占优核”分配方案的稳定性又大大地往前推进了一步。当然,如果想知道这样得到的方案是否具有“核”的稳定性,我们只需要去验证那些非“真子绩效联盟”的稳定性就可以了。
现在,有必要对绩效“集团”博弈中的核进行一番讨论,因为在最新的全面论述合作博弈的书(例如,《Models in Cooperative Game Theory》和《合作博弈引论》)都会介绍模糊“集团”博弈的核的表示式。既然如此,为什么还要去遵循“简单化核”——“占优核”——“真核”——“核”的途径呢?理由很简单,第一,那个表示式需要博弈的特征函数,而且还需要对特征函数在大联盟“点”对于每个非集团成员求“变化率”,这在实际中几乎是做不到的;第二,还是我们在前面强调过的,设计合理的分配方案的目的是鼓励人们百分之百地投入合作;最后,我们将指出,绩效“集团”博弈的核的表示式虽然也涉及到了博弈的特征函数,但是,它需要知道的是每个非集团成员关于大联盟的边际贡献,尽管不知道特征函数,但对他们所做出的边际贡献却是容易估计的。请注意,从Shapley值定义的过程可以知道,分给每个非集团成员的盈利一般不可能达到他关于大联盟的边际贡献,因为这样的话这个人往往“占尽便宜”,通常情况下我们会打个折扣(这个折扣还没有考虑到他的绩效)。譬如说,取非集团成员的边际贡献向量的中心(或者在这一步适当考虑他的绩效),余下的量再分给“集团”成员,是一个可以尝试的想法。此时探索占优核方案就已经相当地方便了。
从以上的研究和陈述,我们发现在考虑绩效因素的社会财富分配问题时,还有许多问题可以进一步思考,譬如:在博弈的特征函数未知情况下使用估计的办法会产生什么样的影响,集团成员如果不全部投入,模型会发生什么变化;另外,绩效本身如何界定,一旦确定了绩效,应该设计什么样的规则,反过来,为了获得公平合理的分配方案,应该如何调整分配规则等等,这些问题都留待我们做深入的研究。
审稿专家对本文提出了非常有益的意见,作者对此表示衷心感谢。文责自负。
参考文献:
[1]何晓斌、夏凡,2012:《中国体制转型与城镇居民家庭财富分配差距》,《经济研究》第2期。
[2]倪迪、符学东,1990:《当前社会收入分配不公问题及其思考》,《管理世界》第6期。
[3]施锡铨,2012:《合作博弈引论》,北京大学出版社。
[4]Aubin, J. P., 1974, "Coeur et Valeur des Jeux Flous a Paiement Lateraux", C. R. Acad. Sci Paris, 279 A: 891—894.
[5]Aubin, J. P., 1981, "Cooperative Fuzzy Games", Mathematics of Operations Research, 6: 1—13.
[6]Branzei, R., D. Dimitrov, and S. Tijs, 2003, "Convex Fuzzy Games and Participation Monotonic Allocation Schemes", Fuzzy Sets and Systems, 139: 267—281.
[7]Branzei, R., D. Dimitrov, and S. Tijs, 2008, Models in Cooperative Game Theory, Springer Press.
[8]Llerena, F., and C. Rafels, 2007, "Convex Decomposition of Games and Axiomatizations of the Core and the D-Core", International Journal of Game Theory, 35: 603—615.
[9]Muto, S., M. Nakayama, J. Potters, and S. Tijs, 1988,"On Big Boss Games", Econom. Stud. Quart., 39: 303—321.
[10]Potters, J., R. Poos, S. Tijs, and S. Muto, 1989, "Clan Games", Games and Economic Behavior, 1:275—293.
[11]Shapley, L. S., 1953, "A Value for N-Person Games", Annals of Mathematics Studies, 28: 307—317.
[12]Tijs, S., and R. Branzei, 2004, "Various Characterizations of Convex Fuzzy Games", TOP 12: 399—408.
[13]Tijs, S., R. Branzei, S. Ishihara, and S. Muto, 2004, "On Cores and Stable Sets for Fuzzy Games", Fuzzy Sets and Systems, 146:285—296.
[14]Tijs, S., R. Branzei, S. Muto, S. Ishihara, and E. Fukuda, 2004, "Fuzzy Clan Games and Bi-monotonic Allocation Rules", Fuzzy Sets and Systems, 146: 271—284.
[15]Yang, Shengming, and Meirui Hao, 2007, "Building a Harmonious Distributive Relationship", Social Sciences in China, 4:137—138.^
