上述两个指标取值均在0和1之间,结果越靠近1表示贸易类型越偏向于产业内贸易,越接近于0则说明贸易越偏向于产业间贸易。自1992年起,中国海关才开始采用HS编码体系,由于数据的可得性以及产品界定上的困难,本文利用HS(1996)二位码产品分类计算我国制造业各分行业的进出口总量,并将黑色金属冶炼及压延加工业,有色金属冶炼及压延加工业和金属制品业统一为金属加工和制品业。制造业总体以G-L指数计算的产业内贸易在2001年左右达到了最高峰,此后有所下降(见图2)。
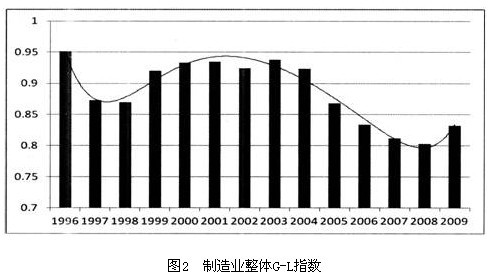
此外,自1995年以来,除纺织服装、鞋帽制造业的产业内贸易G-L指数低于8%,其他各行业在1995年就已经达到非常高的产业内贸易水平,平均水平都在50%以上,纺织业、仪器仪表业甚至达到了97.36%和97.85%。为进一步区分行业特征,本文制造业各细分行业划分为高水平产业内贸易行业和低水平产业内贸易行业,我们针对各行业各年的产业内贸易指数首先计算出每一行业每一年的总体平均值,然后按时间方向计算各行业的产业内贸易指数平均值,如果行业平均值大于总体平均值,则为高产业内贸易水平行业,反之则为低产业内贸易水平行业。表1所示分别为高IIT、高MIIT、高IIT和MIIT行业。
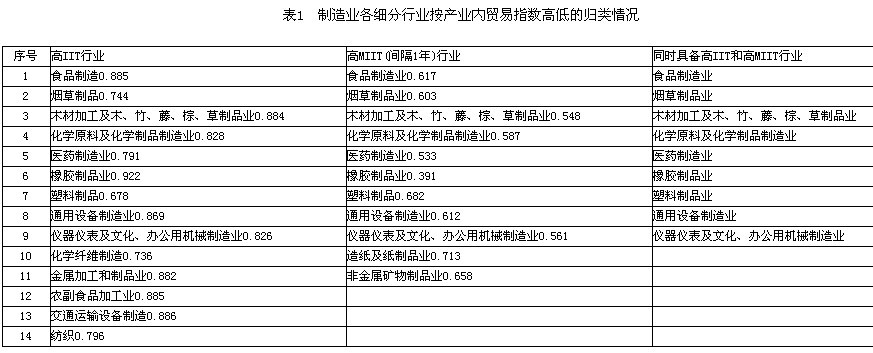
可以看出,各细分行业的产业内贸易指数都非常之高。其中具备高IIT指数的行业有14个,高MIIT指数的行业有11个,占了制造业所有细分行业的50%左右。同时具备两个条件的行业有9个,其中包括食品制造业、烟草制品业、木材加工业以及化学制品制造业等。由此得出如下结论,尽管中国制造业贸易量从2001年开始急剧增加,但在1995年就已经达到相当高的产业内贸易水平,目前我国制造业贸易类型基本以产业内贸易为主。
五、模型构建和数据分析
本节分为三部分,首先讨论回归方程的设定,具体分析各个变量;然后交代数据的来源和处理;最后给出面板数据回归的结论。
(一)回归方程及变量解释
由于我国和马来西亚同是发展中国家,且无法获取个体层面和劳动力相关的详细数据,本文采用Brülhart & Thorpe(2000)的模型:
LWORKERMOVESit=β0+β1×Ait+β2×LTRADEit+β3×LDCONSit+β4×LDPRODit+aj+uit (3)
LWORKERMOVESit==β0+β1×Ait+β2×LTRADEit+β3×LDCONSit+β4×LDPRODit+β5LTRADEit*Ait+ai+uit (4)
回归方程中的因变量为细分行业的总就业量变动的对数,是代表劳动力成本函数。Brülhart & Elliott(2002)采用特定要素模型分析了调整成本的两个来源。该模型假定一小国开放经济,市场完全竞争且价格是给定的,此外,劳动力在部门间可自由流动,但要素是固定的且要素投入递减。由该模型得出了两个调整成本来源:一是由于要素价格缺乏弹性而导致的短期失业,二是由于要素特定性导致的要素价格不一致。平滑调整假说是假设产业内贸易占所有贸易的比例越高,那么劳动力流动的距离和相关的调整成本就越小。一个极端就是所有贸易都是产业内贸易,那么所有的劳动力将只在行业内或者企业内流动,即“短距离流动假设”。因此,行业就业量变动是行业间的就业量变动,应作为劳动力调整成本的反向代表变量①。也就是说,如果SAH有效,那么产业内贸易指数对行业劳动力变动的影响是负向的。即产业内贸易水平越高,劳动力产业内流动成本越低,从而更倾向于产业内流动,而产业间的劳动力流动将越少。
影响劳动力调整的因素有很多,这里主要采取了以下自变量:
LTRADEit指外贸依存度的自然对数,外贸依存度为[(X+M)/Q]。X代表出口,M代表进口,Q为各行业的总产值。对于这个变量的预期为正相关,因为贸易会增加企业间的竞争压力,此时更容易吸收从其他行业转移过来的劳动力,从而使得劳动力的转移成本减少,劳动力变动增加。
LDCONSit为显性需求(Q+X-M)变化绝对值的对数,预期为正。因为消费促进产出增加,企业需要更多的劳动力来进行生产,从而劳动力产业间转移的调整成本降低,促进劳动力产业间流动。
LDPRODit为劳动生产率即人均总产值变动的自然对数,用来替代工资的变动。预期为负相关,因为工资的变动增加,在这个劳动力成本逐渐上升的社会表现为工资的提高,那么劳动力更加不愿意转换工作,其他行业的员工想要进入也需花更多的成本,劳动力的变动就将越少。Erlat(2000)在分析土耳其的时候也证明了这一点。
Ait代表产业内贸易指数,具体以IIT和MIIT两种来表示。根据平滑调整假说,该变量预期为负,产业内贸易指数越高,人员产业内调整成本越低,产业间转移成本就将越高,劳动力的变动也将越小。
LTRADEit*Ait为贸易和产业内贸易指数之间的交叉项,引入该交叉项是因为贸易会促进产业内贸易的增加,其预期影响系数为负。
ai代表固定效应系数。
(二)数据来源和处理过程
本文数据均摘自年鉴以及WTO网站数据库,包括《中国工业经济统计年鉴》、《中国劳动统计年鉴》和《中国统计年鉴》。本次数据涵盖1996-2009年的数据,由于统计年鉴上对个别制造业细分行业的分类不同,导致某些行业数据不全,本文已将这些行业剔除,但并不影响结果。286个样本中包括22个细分行业,13个年份,22个细分行业能足够反应制造业的特征,能够达到本文的目的。
关于产业内贸易指数的计算涉及到产品分类,本文利用HS(1996)二位码产品分类将各产品先归类到相应行业,由于产品界定上的困难,对于个别产业进行了合并,如将黑色金属冶炼及压延加工业,有色金属冶炼及压延加工业和金属制品业统一为金属加工和制品业。这并不影响计量结果,因为本文不需要分析特定行业的特征。接着查询各产品的进出口贸易量进行合计,计算得出我国制造业细分行业的进出口总量和相应的IIT和MIIT指数。与贸易相关的数据均来自WTO网站,由于WTO网站数据库的进出口贸易单位为千美元,对于显性需求和外贸依存度的数据处理按照每年的平均汇率折算后折合人民币所得,显性需求的单位为千元。
(三)回归分析
我们分别使用间隔1年、2年、3年的边际产业内贸易指数来进行对比,以便找到最适合的指数。相应的,对于因变量和自变量中需要做差分的也相应调整了年份跨度。
在对面板数据回归分析之前,首先对其进行Hausman检验,结果显示在1%的置信水平下拒绝原假设,即固定效应是多余的,因此需要在计量分析中采用固定效应模型。其次,为避免计量过程中出现伪回归,分别采用相同根单位根检验LLC(Levin-Lin-Chu)检验和不同根单位根检验Fisher-ADF检验对面板数据进行分析,结果显示,除LTRADE?即贸易依存度为非平稳序列外,其他变量都平稳,因此我们对贸易依存度这个变量做出了适当了调整,将其修整为差分,将原来贸易依存度LTRADE变量修改为DLTRADE,差分后的变量为这一年度的贸易依存度与上一年度之比,不会改变原来变量的意义,重新进行单位根检验并最终通过显著性测试。具体结果(见表2)。
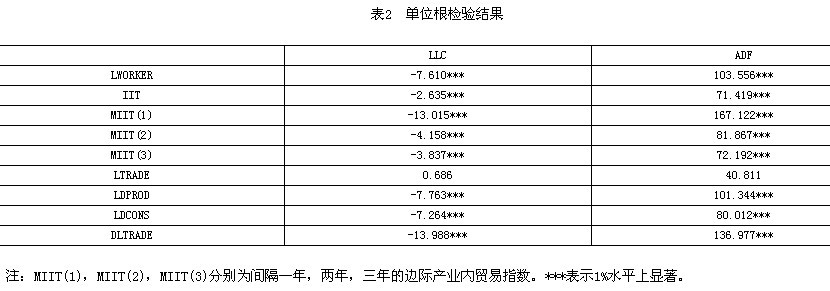
第三,讨论采用何种固定效应模型。固定效应模型分为变参数模型,变截距模型和不变参数模型,其中,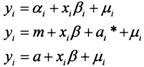
原假设为:
H1:β1=β2=…=βN
H2:β1=β2=…=βN;α1=α2=…=αN
如接受假设H2,则为不变参数模型,若拒绝假设H2,则检验假设H1接受则为变截距模型,拒绝,则为变参数模型。
构建统计量F1,F2,S为对应模型的残差平方和,T为时间跨度总数,N为对应的截面数量,K为自变量的个数。
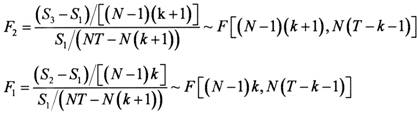
针对不同的产业内边际指数,分别计算F1和F2。根据函数@qfdist(d,k1,k2)可以得到 F(0.95,105,176)=1.3256,F(0.95,84,176)=1.34996,F(0.95,105,154)=1.361,F(0.95,84,154)=1.337。四个不同指数计算的结果均拒绝假设H2,接受假设H1。因此,本文采用变截距模型来进行计量分析。面板数据回归分析结果(见表3和续表3)。
从表3可发现:首先,横向比较IIT和MIIT这两个指标,MIIT(1)完全不显著,MIIT(2)10%水平上显著,MIIT(3)和IIT均在1%水平显著。另一方面,MIIT(3)的拟合优度达到0.916,表明模型整体的解释力度比较大,而含IIT指标的方程拟合优度仅为0.447,因此可知间隔3年的边际产业内贸易指数MIIT(3)比产业内贸易G-L指数IIT更加有效。而且进一步对MIIT(3)进行协整检验,结果均统计显著,说明各变量之间存在着长期稳定的关系,因此该模型反应的是真实的过程。
其次,劳动生产率的系数为正,符合预期假设,劳动生产率越高,劳动力调整成本越高,就业量变动越小。显性需求以及贸易依存度的变动对就业量变动的影响均为正,也符合模型预期的假设。显性需求越高,劳动力流动成本越低,贸易依存度越大,劳动力调整成本也越低。但是无论是IIT还是MIIT,其系数均为正,除间隔1年的MIIT(1)不显著以外,其余各项均显著,交叉项除在MIIT(2)中显著为正外,其余均不显著,结论并不支持SAH,但这一结论在中国并不奇怪,因为贸易是拉动中国经济的三辆马车之一,我国的贸易依存度很高,贸易量一旦增加,行业对劳动力的需求则非常旺盛。为了招到足够的劳动力进行生产,企业在一定程度上会降低行业对特定要素的要求,只要条件较之前优越,劳动力将很容易的进行跨行业流动。因此,尽管在产业内调整对于个人来说更加容易,符合SAH,但是在中国,产业内贸易作为低调整成本的这种贸易形式对于促进劳动力调整并不是必须的。
