我国信贷规模对经济增长影响的定量分析（二）——基于正规金融与非正规金融

需要说明的一点，由于前文分析的分割点得到回归系数只有0.02的差异，结果不显著，而且1994年的分割点的p值也只有0.093，显著性并不是很高，所以为了扩大数据量，提高分析的准确度，在进行协整分析时，仍采用1978—2009年所有的数据分析。

1、变量的平稳性检验

协整分析是要有前提的，首先要满足的一点就是几个变量必须是同阶单整，需先对lnGDP和lnCre进行平稳性检验。

分别观察lnGDP、lnCre的时序图和一阶差分时序图(图2)，可以清晰地看出两个变量水平值不平稳，而一阶差分后平稳。

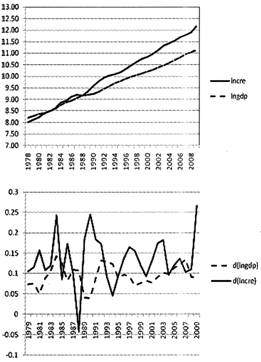
图2 水平时序图和差分时序图

为了更准确地分析两个变量的平稳性，我们进行了单位根检验，检验方法采用Dickey-Fuller的ADF检验，检验结果如表4所示：

表4 各变量平稳性检验

通过表4可以清楚地发现，两个变量的水平值都接受了原假设，即序列是非平稳的，而其一阶差分项都拒绝了原假设，即序列是平稳的，都是一阶单整，记为I(1)。

2、变量协整性分析

协整概念的提出很好地解决了非平稳序列构建动态回归模型可能造成的“伪回归”的问题。协整检验的方法一般有两种：一种是基于回归残差的协整检验，即EG两步法检验；另一种是以VAR模型为基础检验回归系数的协整检验，即JJ检验。由于本文只有两个变量，采用EG两步法就可以很好地解决。

步骤一：建立相应序列与输入序列之间的回归模型：

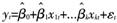(5)

采用最小二乘估计。

步骤二：对回归的残差序列{ε_t}进行平稳性检验。

实证结果分析，利用1978—2009年数据进行回归得到方程：

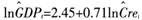(6)

t=(28.68)(84.69)

R²=0.99，DW=0.92

对残差进行ADF平稳性检验，得到ADF=-4.659，对应的p值为0.00，拒绝原假设，认为残差平稳。通过计量分析，我们可以得出银行信贷规模和经济增长是协整的，存在长期均衡关系，长期来看，信贷规模每增长1%，带来经济增长提高0.71%。

3、短期ECM模型

协整分析已经得到了信贷规模和经济增长的长期均衡关系，但实际数据是由“非均衡过程”生成的。因此为了描述短期经济波动，建立误差修正模型(ECM)作为协整分析的补充。其原理即利用上期的误差项ECM_t-1刻画本期波动的原因。

模型结构定义为：

Δy_t＝β₀Δx_t+β₁ECM_t-1+ε_t，也就是说本期的波动Δy_t，主要来自序列当期波动Δx_t、上一期误差ECM_t-1和随机扰动ε_t三方面。

针对GDP，建立的误差修正模型为：

ΔlnGDP_t=β₁ΔlnCre_t＋β₂ECM_t-1＋ε_t，其中β₃表示误差修正项对当期波动的修正力度。

本文利用差分序列{ΔlnGDP_t}，{ΔlnCre_t}和前期误差序列{ECM_t-1}构建ECM模型：

ΔlnGDP_t=β₁ΔlnCre_t+β₂ECM_t-1+ε_t (7)

利用Eviews得：

ΔlnGDP_t=0.59ΔlnCre_t-0.43ECM_t-1 (8)

t=(10.37) (2.94)

上述方程中误差修正模型的系数为负，说明符合误差修正机制是一个负反馈机制。参数检验结果显示信贷规模的当期波动和上期的误差对GDP的当期波动有显著影响。从回归系数的绝对值上看，短期银行信贷规模每提高1个百分点，则GDP增加0.59百分点，说明信贷规模的变动对GDP增长的影响效应明显，上一期误差(ECM)对GDP的当期波动调整幅度较大，调整的比例为43%。

4、格兰杰因果关系分析

既然lnGDP和lnCre存在协整关系，则彼此之间就存在格兰杰因果关系，即检验某个变量的变化是否是另一个变量变化的原因。其检验方法是借助VAR模型，利用残差平方和检验一个变量是否可以引入其他变量的方程中。本文做了滞后4期的检验，其检验结果如表5所示：

表5 格兰杰因果关系检验

通过检验结果我们可以发现，信贷规模滞后四期都是GDP的格兰杰原因，GDP在滞后两期和四期是信贷规模的格兰杰原因。即信贷规模的变动可以引起GDP的变动，GDP的变动对信贷规模的影响存在滞后性，但也可以反向影响其变动。结果验证了信贷规模对经济增长有显著影响，经济增长带来了国内环境的稳定，从而也就有利于信贷发展。

三、非正规金融信贷规模的绩效分析

银行信贷规模，即政府所记录的各类银行、投资机构的数据，属于正规贷款路径。但贷款的发生，还应包含发生在官方监管之外的信贷活动，尤其是我国现阶段还存在政策紧缩、金融抑制的状况，非正规金融信贷的存在、发展是现阶段金融发展的补充。

(一)非正规金融的内涵及其成因

对于非正规金融的定义和内涵，国内学者并未统一，很多时候也称“地下金融”、“体制外金融”等；国外学者对“非正规金融”的定义较为统一。根据德布拉吉·瑞(Debraj Ray)的《发展经济学》的定义：“非正规金融”指金融体系中没有受到国家信用控制和监管当局监管的金融交易活动，包括非正规的金融中介和非正规的金融市场。^⑤由于我国市场经济尚未发达，金融产品匮乏，所以在本文中定义“非正规金融”为由民间资本支撑的信用体系，可以简单理解为民间信贷。“非正规金融”的存在是对我国金融抑制的理性反映，是中小型企业融资困境的有效解决途径。Strahan和Weston(1996)提出的规模匹配模型指出，银行对小企业的贷款与银行的规模之间存在很强的负相关性，即大金融机构通常更愿意为大企业提供融资服务而不愿意为资金需求规模小的小企业提供融资服务。

银行歧视行为的存在，推动了非正规金融信贷的发展。非正规金融发展之初，是发生在熟人之间，并且需求者为了获得资本，而愿意付出比银行更高的成本，即利息；供给者凭借对需求者的了解与信任，并能获得高于银行的利息，同样乐意将资本出借。高利润率，低风险，成为了非正规金融发展初期的特点与优势。正是凭借这样的发展优势，其规模才能发展迅速，成为经济增长的另一重要变量。

(二)政府对非正规金融的态度分析

首先分析非正规金融和正规金融的边际贷款成本，非正规金融在我国基本上是发生在熟人之间，但是随着非正规金融规模的扩大，贷款范围会扩展到非熟人，从而会增加贷款成本、管理成本，所以非正规金融的边际贷款成本先下降后上升，呈现“U”型，与之对应的正规金融随着客户数量增加，边际贷款成本呈下降趋势。^⑥

为了考察政府对非正规金融的态度，王曙光(2010)提出了政府的金融效用函数：

U(x)=w_if_i(x)＋w_gf_g(1-x)

其中，x表示非正规金融机构所占有金融资源的比例，1-x表示政府金融机构所占的金融资源比例，f_i(x)、f_g(1-x)分别表示非正规金融和正规金融对社会总产出的贡献度，w_i、w_g表示政府对两种金融机构的偏好程度。可以假设，政府偏好于正规金融机构，则可令w_g=1，w_i＜1，则政府效用函数可以简化为：U(x)=w_if_i(x)+f_g(1-x)。

要改变政府对于非正规金融的抑制水平，则需要保证Δx(Δx＞0)改变后，能够保证政府的效用ΔU(x)＞0，即：

ΔU(x)=U(x＋Δx)-U(x)

=[w_if_i(x＋Δx)+f_g(1-x-Δx)]-[w_if_i(x)+f_g(1-x)]

=w_i[f_i(x＋Δx)-f_i(x)]-[f_g(1-x)-f_g(1-x-Δx)]＞0

为了保证ΔU(x)＞0，则：w_i[f_i(x＋Δx)-f_i(x)]＞[f_g(1-x)-f_g(1-x-Δx)]

当Δx变化很小时，可以用导数近似表示上式：w_if_i^′(Δx)>f_g^′(1-x)Δx

即：w_if_i^′(x)>f_g^′(1-x)

这就是说，当政府对非正规金融偏好与非正规金融的边际贡献度乘积大于政府边际贡献度时，才会采取调整非正规金融资金比例，也就是才放宽对非正规金融的抑制。

为了分析政府抑制非正规金融信贷规模带来的后果，从姜旭朝、丁昌锋(2004)提出的边际贷款成本进一步分析(图3)，图中为了得到两个边际成本函数的交点，将政府正规边际成本曲线进行了左右转置。在政府进行金融抑制的情况下，非正规金融的边际成本会整体上升。

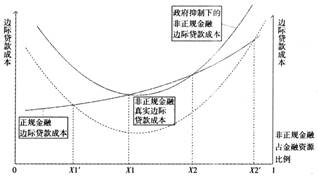
图3 非正规金融融资规模比例分析

在政府抑制下，为了保证政府效用函数，在w_if_i^′(x)>f_g^′(1-x)条件下，非正规金融规模限制在X1和X2之间。但是，在不存在政府抑制时，非正规金融的发展限度可以扩大到X1’和X2’之间。

(三)非正规金融的实证分析

政府对非正规金融的抑制导致了其规模的扩大，在我国实际状况如何，需要做进一步计量分析

1、非正规金融规模估算

蒙替尔和阿发诺尔(Montiel和Agenor，1994)的《发展中国家的非正规金融市场》一书中估算，我国非正规金融占借款总量的33%—67%；蔡(Tsai，1999、2001)认为我国乡村非正规金融信贷总量占正规金融的25%^⑦，非正规金融交易参与率占总人口的20%左右。李建军和田光宁(2005)借鉴国民经济核算体系(SNA)，认为经济核算中存在一个“非正规经济金融部门”，采用国民核算的公式，粗略估计了1982—2003年“非正规经济金融部门”的资金流量，本文就采用其估算的值作为计量分析的“非正规金融”规模。数据如表6所示：

表6 非正规金融规模

资料来源：李建军、田光宁：《非正规经济金融部门资金净流量规模测算》，《统计研究》2005年第4期，第30页

2、非正规金融的协整分析

对于非正规金融(变量设为lnInf)仍采用和正规金融同样的分析方法，分析其对经济发展的影响，分析结果如表7所示：

表7 变量平稳性检验

平稳性检验发现非正规金融也是水平数据不平稳，一阶平稳，适合做协整分析。采用EG两步法，得出残差的ADF值为-5.516，对应p值为0.001，即非正规金融和经济发展也具有协整关系。长期和短期ECM模型为：

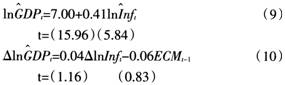
长期看来，非正规金融每增长1%，GDP增长0.41%。短期看，误差修正模型的系数为负，说明符合误差修正机制是一个负反馈机制。参数检验结果显示金融发展的当期波动对GDP的当期波动有显著影响。从回归系数的绝对值看，短期金融发展每提高1个百分点，则GDP增加0.04百分点，说明金融发展的变动对GDP增长的影响效应明显。但上一期误差(ECM)对GDP的当期波动调整不显著，幅度也不大，调整的比例为6%。通过以上分析，可以得到非正规金融与经济增长同样有显著的相互影响。

责任编辑：夏雨