联合生产中的价值决定（二）

二、联合生产：数字例子
    现在来看联合生产的情况。同样设某行业只包括两个企业，且两个企业投入的劳动量分别为15个和25个单位，但同时生产两种商品。具体来说，企业1生产的商品1的数量为15，商品2的数量为10，企业2生产的商品1的数量为15，商品2的数量为40。从而，整个行业投入的劳动量为15+25=40，生产的商品1的数量为15+15=30，商品2的数量为10+40=50。参见表2。(14)
    
    此时，非联合生产中决定单位商品价值的公式(1)不再适用，因为在这种情况下，不是只有一种商品，而同时有两种商品，相应的，也不是只有一种商品的价值需要决定，而是同时有两种商品的价值需要决定。
    下面先把非联合生产条件下关于价值的三条性质，即公式(3)、(4)和(5)，推广到联合生产中去，然后再根据推广后的这些性质，来计算联合生产中每个企业创造的价值和每种商品的价值。
    首先容易看到，在非联合生产条件下关于价值的性质1，即在同一行业中，所有企业创造的价值之和等于它们投入的劳动之和，在联合生产条件下，仍然具有相同的形式。例如，在表2所给的联合生产的数字例子中，由于企业1和企业2投入的劳动总量为15+25=40，故它们创造的价值之和也等于40，即有：
    
    这里需要说明的是，由于现在讨论的不再是单独一种商品，而是同时包括两种不同商品在内的联合商品，故行业的概念应当重新定义为“所有生产相同的联合商品的企业的集合”。
    其次，由于在联合生产中，每个企业都同时生产多种商品，故在非联合生产条件下关于价值的性质2，即任何一个企业创造的价值等于它生产的商品数量和单位商品价值量的乘积，在联合生产的条件下应当推广为，任何一个企业创造的价值等于它所生产的各种商品的数量与相应的单位商品价值量的乘积之和。例如，在表2所给的联合生产的数字例子中，若设商品1和商品2的单位价值量分别
    
    
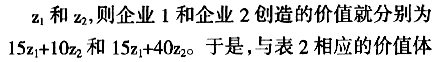
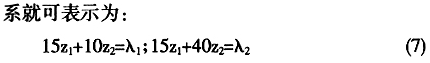
    从这里也可以看到，尽管在联合生产和非联合生产中，关于价值的性质1的表现形式是完全一样的，但其包含的内容却有所不同，因为在联合生产的条件下，每个企业创造的价值不再是它生产的单一商品的数量与价值的乘积，而是其全部商品的数量与价值的乘积之和。
    
    在联合生产中，由于每个企业生产的不再是单独一种商品，而是同时包括多种商品在内的联合商品，故现在也不再是只有一种商品的产出比，而是同时有多种商品的产出比。例如，在表2中，有根据商品1计算的产出比15/15=1和根据商品2计算的产出比40/10=4。但是，这些产出比都是“局部”的和“个别”的，不能代表联合商品(亦即把商品1和商品2放在一起考虑)的综合的产出比。考虑到这一点，在非联合生产条件下关于价值的性质3，即在同一行业中，不同企业创造的价值之比等于它们的产出之比，在联合生产条件下需要修正为“在同一行业中，不同企业创造的价值之比等于它们的联合商品的综合产出比”，其公式表示如下：
    
    
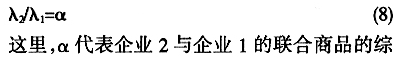
    特别是，当联合产出比位于两种商品的个别产出比之间，即1＜α＜4时，两种商品的价值都大于0。这是通常所见的联合生产情况。其他一些特殊情况则包括：当联合产出比恰好等于较大的商品2的个别产出比，即α=4时，商品2的价值大于0，商品1的价值等于0；当联合产出比大于较大的商品2的个别产出比，即α＞4时，商品2的价值大于0，商品1的价值小于0；当联合产出比恰好等于较小的商品1的个别产出比，即α=1时，商品1的价值大于0，商品2的价值等于0；最后，当联合产出比小于较小的商品1的个别产出比，但仍然大于0，即0＜α＜1时，商品1的价值大于0，商品2的价值小于0。
    
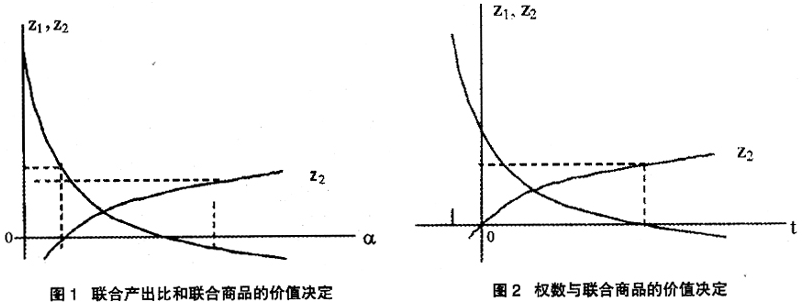
    现在的问题是，联合产出比α应当如何决定？容易想到，它应当从所有的单个商品的个别产出比中“综合”而成。例如，我们假定联合产出比是所有个别产出比为1和4的加权平均：α=1(1-t)+4t。这里，1-t和t分别是赋予商品1和商品2的个别产出比的权数(简称商品1和商品2的权数)。
    由于联合产出比必须为正数，即α＞0，故1(1-t)+4t＞0。这意味着t＞-1/3，或者1-t＜4/3。换句话说，为了保证所有企业创造的价值均大于0，亦为了保证联合产出比为正数，赋予个别产出比较大的商品2的权数必须大于-1/3，或者说，赋予个别产出比较小的商品1的权数必须小于4/3，否则就会导致至少有一个企业所创造的价值为0甚至为负的结果。
    将上述关于联合产出比的权数表达式代入公式(10)可得：
    
    由此可见，在联合生产中，某种商品的价值是大于还是小于或等于0取决于赋予它的权数为正还是为负或是为0。例如，当赋予商品2的权数t大于、等于和小于0时，商品2的价值大于、等于和小于0。现在要进一步问的是：这些权数又是如何决定的？同样容易想到，赋予某一商品的权数的大小依赖于该商品本身的性质，例如，它们是有用品还是无用品或有害品。
    先来看权数为0的情况。如前所说，在联合生产中，如果赋予某种商品的权数为0，则该商品的价值就为0。这个结果也可以反过来说：如果某种商品的价值为0，则赋予它的权数也应当为0。
    那么，在什么样的情况下，商品的价值会为0呢？根据马克思的劳动价值论，有两种可能：要么该商品不是劳动产品，其中不包含劳动；(16)要么该商品不是有用产品，没有使用价值。(17)由于在我们所讨论的联合生产中，企业是在联合商品上耗费的劳动，从而，也就是在每种商品上都耗费了劳动，故剩下的唯一可能就是：价值为0的商品是一种“无用品”，即没有使用价值的商品，如在生产过程中产生的某些无害的废弃物。由于不具有使用价值，故对无用品而言，在它上面耗费的劳动不能形成价值，从而，在确定联合产出比时，没有必要去考虑无用品的个别产出比。这意味着，在计算联合产出比时，赋予无用品的权数应当等于0。
    一旦允许在联合生产中出现无用品，则许多传统上常常被看成非联合生产的情况亦可以作为联合生产来处理。例如，考虑一个在生产合格产品的同时也有相当数量废品的非联合生产。我们可以把这里的合格品和废品看成是同一个生产过程中生产的联合产品。由于在这种联合生产中，废品没有使用价值，因而也没有价值，赋予它的权数为0，或者说，联合产出比完全取决于合格品的个别产出比，而与废品没有任何关系。
    又如，生产单一产品的非联合生产过程除了需要劳动投入之外，还需要投入机器等固定资本。这些固定资本在一个生产过程之后，其价值的一部分会转移到产品中去。我们可以把转移掉的价值部分看成生产过程的“投入”，而把剩余的部分(未被消耗掉的机器——它已经不同于原来的机器)看成生产过程的“产出”。这样，在一个生产过程结束之后，我们除了得到一部分原来意义上的产品之外，还得到一个由于折旧而价值已经有所减少的机器。因此，若把这样的机器也看成一种产出的话，则我们面临的就是一个既生产普通意义上的产出又生产价值已经改变的机器的联合生产过程。(18)特别是，在机器折旧完毕的最后一个生产周期中，由于我们得到的除普通产品之外是一个机器残骸，故我们面临的是一个包括无用品的联合生产过程。(19)
    根据赋予使用价值为0的无用品的权数应当为0的理由，容易得到如下的推论，即赋予使用价值大于0的“有用品”的权数应当大于0，而赋予使用价值小于0的“有害品”的权数应当小于0。
    首先来看有用品。由于有用品具有使用价值，故在生产它们时耗费的劳动能够形成价值，从而，在计算联合商品的综合产出比时，赋予所有有用品的权数都应当大于0。例如，设商品1和商品2均为有用品，则赋予它们的权数1-t＞0且t＞0。这意味着0＜t＜1且0＜1-t＜1。换句话说，在联合生产中，如果所有的商品都是具有使用价值的有用品，则联合商品的综合产出比就不会超出由个别产出比限定的范围。
    其次来看有害品，如在生产有用品的过程中产生的污染物。由于有害品不仅没有使用价值，反而会有负的使用价值，故在它上面耗费的劳动(尽管有时是必要的)不仅不形成价值，反而会带来“负”的价值，即起着抵消有用品的价值的作用。因此，在计算联合商品的综合产出比时，赋予有害品的权数应当小于0。例如，设商品1是有用品，商品2是有害品，则1-t＞0但t＜0。(20)
    前面说过，为了保证所讨论的联合生产有意义，要求联合产出比大于0，即α＞0。如在表2所给的数字例子中，要求赋予个别产出比较大的商品2的权数t＞-1/3，或者要求赋予个别产出比较小的商品1的权数1-t＜4/3。现在可以看到，当商品1和商品2都是有用品，或者，其中一个为有用品而另一个为无用品时，这些要求自然满足，但是，当其中一个为有害品时，情况就比较复杂。
    可见，当有害品的个别产出比较小时，无论赋予它的权数如何，联合产出比都不会小于0，从而，所有企业创造的价值都不会小于0。例如，在表2的数字例子中，只要赋予个别产出比较小的商品1(这里假定它是有害品)的权数小于4/3，则联合产出比就大于0——由于赋予有害品的权数总小于0，故它一定小于4/3。
    但是，当有害品的个别产出比较大时，特别是当有害品的有害程度还相当大时，联合产出比就有可能小于0。例如，在表2的数字例子中，当商品2(这里假定它是有害品)的权数小于-1/3时，联合产出比就将小于0——由于赋予有害品的权数小于0，故它有可能小于-1/3。
    从这里可以看到，在联合生产中，可以允许出现有害品，但需要满足一个条件，即有害品的有害程度不能过大，否则，赋予它的权数的绝对值就会过大，从而导致联合产出比小于0。在这种情况下，总有一个企业所创造的价值为负数，从而，该企业事实上没有存在的必要。当然，当某个企业创造的价值为负数时，由于整个行业创造的价值总是正的——它等于整个行业投入的劳动总量——故另一个企业创造的价值仍然为正数。
    根据上述讨论，可以把这里给出的联合生产条件下的价值决定方式看成非联合生产中劳动价值论的发展和推广。例如，在非联合生产中，所讨论的商品不能为无用品或有害品，否则，该生产就是没有意义的。同样，在联合生产的条件下也有类似的要求，即不能所有的商品都为无用品或有害品(尽管允许其中某种商品是无用品或有害品)，或者说，至少要有一种商品为有用品，否则，所有商品的价值都将为0或负数，从而，所有企业以及整个行业创造的价值都将为0或负数。这样的联合生产当然是没有意义的。(21)此外，当所讨论的商品中存在有所谓的有害品时，有害品的有害程度不能过大，否则，赋予它的权数(的绝对值)就可能过大，导致联合产出比小于0，从而，使某个企业创造的价值小于0。换句话说，如果有害品的有害程度过大，则即使同时也存在有用品，相应的联合生产也是没有意义的。总之，在联合生产中，既可以包括有用品，也可以包括无用品甚至有害品，只要不是所有的商品都为无用品或有害品，且在同时存在有用品和有害品时，有害品的有害程度不是过大即可。此外，当我们把联合生产当做非联合生产，即只考虑联合生产中的某一种商品而不考虑另外一种商品时，则前一种商品的价值决定就如同非联合生产中的情况一样，而后一种商品的价值就等于0。例如，在表2的例子中，当我们不考虑商品2(即令赋予商品2的权数t等于0，或者，令联合产出比等于商品1的个别产出比，即α=15/15=1)时，商品2的价值就等于0，而商品1的价值为=4/3；另一方面，当我们不考虑商品1(即令赋予商品1的权数1-t等于0，或者，令联合产出比等于商品2的个别产出比，即α=40/10=4)时，商品1的价值就等于0，而商品2的价值为=4/5。它们恰好等于非联合生产条件下每种商品的价值量。这意味着，如果我们把两种商品的联合生产看成关于一种有用品和一种无用品的联合生产，则得到的结果就与只考虑有用品的非联合生产完全一样。这是因为，在价值的决定中，无用品的产出比是没有意义的，故联合产出比完全由有用品的产出比决定，从而，无用品的价值为0，而有用品的价值为正，且该有用品的价值恰好等于整个行业投入的劳动总量与有用品总量的比。
    上述基于表2的讨论可以总结如下：在联合生产中，由于赋予有用品、无用品和有害品的权数应分别大于、等于和小于0，故对于只有两种商品的联合生产来说，如果两种商品都是有用品，则赋予它们的权数1-t和t都大于0，于是有0＜t＜1，从而，联合产出比必位于两种商品的个别产出比之间，即1＜α＜4，结果，两种商品的价值都将为正数，即＞0、＞0；如果在两种商品中，商品1是有用品、商品2是无用(或有害)品，则赋予商品1的权数大于0、赋予商品2的权数等于(或小于)0，于是有t=(＜)0，从而，联合产出比必等于(或小于)商品1的个别产出比，即α=(＜)1，结果，商品1的价值大于0、商品2的价值等于(或小于)0，即＞0、=(＜)0；另一方面，如果在两种商品中，商品2是有用品、商品1是无用(或有害)品，则赋予商品2的权数大于0、赋予商品1的权数等于(或小于)0，于是有1-t=(＜)0，或者，t=(＞)1，从而，联合产出比必等于(或大于)商品2的个别产出比，即α=(＞)4，结果，商品2的价值大于0、商品1的价值等于(或小于)0，即＞0、=(＜)0。
    以上讨论的是权数的“质”，即它的取值范围。同样也可以确定权数的“量”，即它的具体大小。例如，设商品1和商品2均为有用品。由于商品1和商品2是两种不同的产品，故尽管它们是由同一个行业生产出来的，但仍然分属于两个不同的市场。因此，在它们之间存在着(直接的或间接的)交换关系。若假定1个单位的商品2恰好交换2个单位的商品1，则可以令赋予商品2的权数为赋予商品1的权数的2倍，即有t=2(1-t)。解之即得t=2/3、1-t=1/3。(22)于是，联合产出比为α=1(1-t)+4t=1×(1-2/3)+4×2/3=3。相应的，商品1和商品2的价值分别为：
    
    
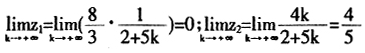
    结果与以前完全相同：赋予有用品(商品2)的权数为1，赋予无用品(商品1)的权数为0，联合产出比等于有用品(商品2)的个别产出比(α=4)，无用品(商品1)的价值为0，有用品(商品2)的价值大于0。
    当商品2为有用品而商品1为有害品时，我们先假定存在一个刚好能够抵消有害品的负面影响的有用品——可称该有用品为“中和有用品”，或简称“中和品”。显然，1单位的商品1(有害品)相当于-1个单位的中和品。在这种情况下，如果1单位的商品2(有用品)交换k单位的中和品，则即可按上述方法求出中和品以及商品2的价值，而中和品价值的相反数就是商品1(有害品)的(负)价值。