时变弹性生产函数生产率分解公式及其政策含义

内容提要：本文基于时变弹性生产函数，推导出经济增长来源于资本、劳动力、中性技术进步和偏向性技术进步贡献度之和；“索洛余值”在数值上等于中性技术进步贡献度与偏向性技术进步贡献度之和，也等于资本生产增长率与劳动生产增长率的加权和，其权数分别为资本和劳动时变产出弹性。研究认为，提高劳动收入份额，有利于促进经济向集约型发展方式转变。
    关键词：时变弹性生产函数/偏向性技术进步/劳动收入份额/全要素生产率
    作者简介：章上峰，浙江工商大学数量经济研究所
    引言
    经济增长是社会发展的前提，生产率分析是探求增长源泉的主要工具，其中全要素生产率测算是生产率分析的中心内容，也是确定增长质量的主要方法。1957年美国经济学家罗伯特·索洛在《经济学与统计学评论》上发表了名为《技术进步与总量生产函数》的经典文章，提出了基于总量Cobb-Douglas生产函数的全要素生产率增长率测算的索洛余值法，从而开创了经济增长源泉分析的先河。
    生产函数是描述生产过程中投入生产要素的某种组合与它可能的最大产出之间依存关系的数学表达式。Cobb-Douglas生产函数具有结构简单、经济意义明显且容易估计等优点，因而受到广泛应用。利用Cobb-Douglas生产函数估计得到的产出弹性α和β值是固定常数，它刻画了新古典稳态经济增长模型中生产要素分配份额具有较强的时间稳定性特征(Solow，1956、1958；Cass，1964；Lucas，1988；Romer，1986、1990；Gollin和Williams，2002；Leandro和Joan，2003)，并在实践上得到卡尔多(Kaldor，1961)归纳的20世纪主要发达国家经济增长的六个“典型事实”(Stylized Facts)的有力支撑：(1)劳动生产率稳速增长；(2)劳均资本稳速增长；(3)资本回报率(实际利率)稳定；(4)资本产出比稳定；(5)国民收入中资本份额和劳动力份额保持稳定；(6)不同国家劳动生产率和产出增长率存在差异。尽管这一教条不断受到质疑，但仍然有很多人将它视为“像‘光速’一样恒常不变的东西”(Solow，1957；Kravis，1959)，卡尔多事实也已经从研究论文写入教科书中，在卡尔多之后，经济增长基本沉迷于“稳定状态”的模型推导之中(张平，2006)。
    但是，近年来一些国家和地区劳动收入份额的变化趋势并不符合“卡尔多事实”。Blanchard(1997)利用OECD企业部门数据(OECD Business Sector Data)计算劳动收入份额时发现，该值至少在中期内不是一个常数；Poterba(1997)发现20世纪80年代至20世纪90年代，法国、德国和意大利的劳动收入份额呈下降趋势；Hofman(2001)发现自1950年至20世纪90年代末拉美国家劳动收入份额在这50年间呈下降趋势；Bentolina和Saint-Paul(2003)发现，1970-1993年13个OECD国家除英国比较稳定外，其余各国劳动收入份额变化各不相同。此外，无论是C-D生产函数，还是CES函数，都很难解释过去20年内欧洲大陆国家劳动收入占比所发生的变化。在这些国家中，劳动和资本之间的替代弹性接近于1(Blanchard，1997)，但是劳动收入份额却不是一个不变的值(罗长远，2008)。我国处于经济转型时期，随着生产要素的流动限制减少和价格放开，资本和劳动力的数量与价格是逐期变化的，因而不同时期的资本和劳动力份额也会存在一定程度的变化(章上峰、许冰，2009、2010)，根据省际收入法GDP核算数据，近年来我国劳动收入份额也出现不断下降的趋势，从1995年的51.44％下降至2008年的39.50％，共降低了11.94个百分点。Charles I. Jones和Paul M. Romer(2010)提出了体现现代经济增长典型特征的“新卡尔多事实”。
    利用Cobb-Douglas生产函数估计得到的α和β值是固定常数，它们反映的只是整个研究时期的平均产出弹性水平，然而未能反映不同时期资本和劳动力的收入份额的变化。因此，该方法仅适用于估计整个研究时期的资本、劳动力和全要素生产率的平均贡献率，但是用于估计逐期贡献率很可能是有偏的甚至有误的(章上峰、许冰，2009)。章上峰、许冰(2009)从资本和劳动力产出弹性的时变性出发，提出利用时变弹性生产函数模型代替收入份额法确定不同时期资本和劳动力的时变产出弹性，从而为科学计算全要素生产率提供了新的方法和视角。本文进一步利用时变弹性生产函数模型，分解资本、劳动力、中性技术进步、偏向技术进步和全要素生产率对经济增长的贡献度，探讨技术进步偏向引致资本和劳动力产出弹性变化对资本、劳动力和全要素生产率贡献度的影响。
    一、时变弹性生产函数模型
    常用的Cobb-Douglas生产函数表达式如下：
    
    其中，P、r和w分别表示实际产出、资本和劳动力的价格水平。
    模型是对现实的模拟，生产函数模型是对生产活动中产出量与投入要素组合之间关系的模拟。模型总是建立在一定的假设基础上的，没有假设，就没有模型。而假设与现实之间是有差距的，这个差距越小，说明模型对现实的描述越准确。假设不断向现实逼近，导致模型不断发展(李子奈、叶阿忠，2004)。早期对于C-D生产函数模型的拓展研究，主要关注要素的替代弹性，不变替代弹性生产函数(CES)和可变替代弹性生产函数(VES)放宽C-D生产函数模型的假设条件，超越对数生产函数(Translog)则是一个更具一般性的变替代弹性生产函数模型：
    
    但是超越对数生产函数模型由于待估参数过多，容易带来自由度不足、多重共线性等统计计量问题；此外，在参数确定的情况下，资本和劳动力产出弹性分别是资本和劳动力投入量的指数线性组合函数，这一假设经常是不合理的。
    随着现代计量经济学的发展，使得合理构造生产函数模型，用于估计不同时期资本和劳动力产出弹性成为可能。Shigeru Iwata等(2003)、赵志耘等(2006)、Bing Xu和Berlin Wu(2007)提出时变产出弹性的非参数估计方法，高宇明和齐中英(2008)、章上峰和许冰(2009)提出时变产出弹性的可变参数卡尔曼滤波估计方法，章上峰和许冰(2009)提出时变产出弹性的变系数面板数据估计方法，Ahmad等(2005)、章上峰和许冰(2009，2010)、罗羡华等(2009)、许冰(2010)将产出弹性看作非参数光滑函数，提出时变产出弹性的变系数估计方法。变系数生产函数模型和可变参数生产函数模型，沿用人们熟悉的不变参数Cobb-Douglas生产函数形式，拓展为变参数Cobb-Douglas生产函数，具有明确的数学表达式，估计得到的分别代表t时期资本和劳动力时变产出弹性，符合经济学意义(章上峰、许冰，2009)。章上峰等(2011)利用统计学和经济学检验得出时变弹性生产函数模型是更加符合实际的生产函数模型。本文借鉴章上峰和许冰(2009，2010)、罗羡华等(2009)将产出弹性看作时间t的非参数光滑函数，构造产出弹性时变的时变弹性生产函数模型：
    
    α(t)和β(t)是时间t的非参数光滑函数系数，分别代表不同时期t的资本和劳动力产出弹性。时变弹性生产函数改进了Cobb-Douglas生产函数产出弹性固定不变的假设，因此是一个更具一般性的生产函数模型。
    模型(11)本质上是一种半参数变系数模型，该模型的优点之一是避免“维数灾难”，同时可以避免先验模型设定错误。变系数部分关于回归变量仍是线性的，但其系数是所有n个回归变量观测值所对应观测时间位置中的函数，除包含回归变量本身的观测值信息外，还含有观测点“时间位置”的信息。半参数变系数模型常用的估计方法主要包括Backfitting估计方法(花俊洲等，2003)，Efficient估计方法(Ahmad，2005)和Profile估计方法(Fan和Huang，2005)等。由于局部多项式估计具有较好的统计性质，本文采用Fan和Huang(2005)提出的Profile局部多项式估计方法来估计未知参数和函数系数值。
    
    则式(11)可写为：
    
    利用Profile局部多项式方法，可以得到未知参数γ和函数系数α(t)和β(t)的最终估计值。
    二、一个新的生产率分解公式
    Hicks(1932)在《工资理论》中将技术进步定义为要素边际生产力的提高，具体表现为成本的节约或最佳要素投入组合点的移动。假定要素价格比率保持不变，技术进步一方面会减少某一产出水平所需的要素投入量，从而降低成本；另一方面也会改变要素投入比率，使产品的要素密集度发生变化。假设只有资本和劳动力两个生产要素，技术进步可以分为希克斯中性技术进步、资本偏向型技术进步和劳动偏向型技术进步三种类型。通常根据相对资本密集度w(资本弹性和劳动弹性比)来判断技术进步类型，在技术进步前后，如果相对资本密集度w保持不变，则称为中性技术进步；如果相对资本密集度w保持变小，则称为资本偏向型技术进步；如果相对资本密集度w保持不变，则称为劳动偏向型技术进步。相对资本密集度的变化必然表现为资本和劳动产出弹性的变化。根据前后两个时期，技术进步是否导致资本和劳动产出弹性发生变化，是判断是否发生技术进步偏向的前提依据。
    考虑连续时间情况，时变弹性生产函数经济增长率分解公式为：
    
    
    式(26)～式(28)表明，全要素生产率增长率，即资本投入和劳动力投入不能解释的“索洛余值”，在数值上等于中性技术进步增长率与偏向技术进步增长率之和，等于产出增长率减去资本投入和劳动力投入增长率的加权和，还等于资本生产率增长率
    
    在不变规模报酬假定下，资本产出弹性等于资本收入份额，劳动产出弹性等于劳动收入份额。偏向性技术进步引致资本和劳动力产出弹性变化，从而直接影响内涵贡献率和外延贡献率。为了便于讨论，本文以下假定资本、劳动力和经济增长率保持不变，考察资本和劳动力弹性变化对内涵贡献率和外延贡献率的影响。
    如果第t期资本产出弹性α(t)变化Δα(t)，同时劳动产出弹性变化-Δα(t)，此时内涵贡献率等于：
    
    
    在不变规模报酬假定下，资本产出弹性等于资本收入份额，劳动产出弹性等于劳动收入份额。时变弹性生产函数生产率分解模型，对经济发展方式转变具有重要的政策启示意义：通常情况下，资本增长率高于劳动增长率，如果提高资本份额、降低劳动份额，即提高资本产出弹性、降低劳动产出弹性，将提高资本贡献率，降低劳动贡献率，提高外延贡献率，降低内涵贡献率，从而导致经济向粗放型发展方式转变，不利于经济可持续增长。反之，如果降低资本份额、提高劳动份额，即降低资本产出弹性、提高劳动产出弹性，将降低资本贡献率，提高劳动贡献率，减少外延贡献率，提高内涵贡献率，从而促进经济向集约型发展方式转变，有利于经济可持续增长。
    四、经验研究
    在不变规模报酬假定下，产出弹性符合经济学收入份额概念，即资本产出弹性等于资本收入份额，劳动产出弹性等于劳动收入份额；不变规模报酬假定还可在一定程度上消除资本和劳动力可能存在的共线性问题。
    经验研究使用1978-2008年中国统计数据：(1)国内生产总值Y(单位：亿元)：以1952年为基期的实际国内生产总值表示；(2)资本存量K(单位：亿元)：1952年基期资本存量采纳张军等(2004)的估算结果为807亿元，经济折旧率采纳张军等(2004)方法取9.6％，参考曹吉云(2008)研究方法，法定残值率取4％，以年初固定资本存量和年末固定资本存量的简单算术平均作为资本投入量；(3)劳动力投入L(单位：万人)：以年初和年底就业人员数的平均值表示；(4)中性技术水平由常数项Z[，1]、市场化程度Z[，2](非国有经济在工业总产值中的比重)和经济结构Z[，3](第三产业劳动力投入占比)的线性组合表示。以上数据来自《中国统计年鉴2009》、《中国国内生产总值核算历史资料》和《新中国五十五年统计资料汇编》。
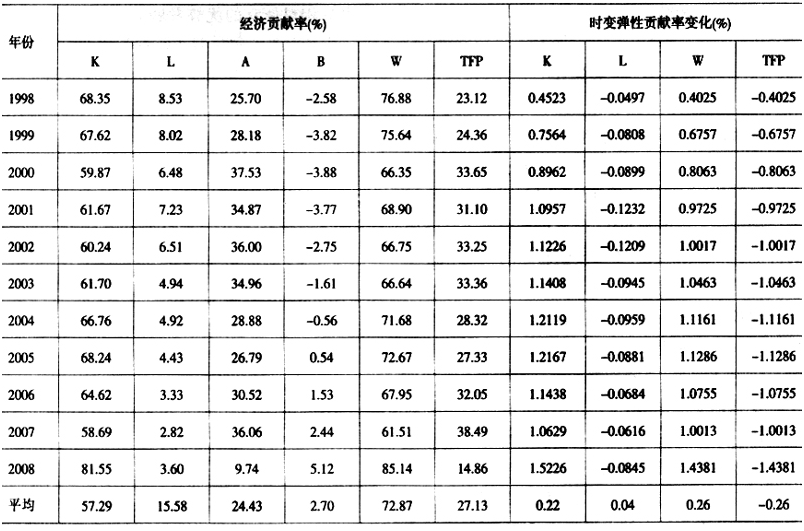
    采用Fan和Huang(2005)的Profile估计方法，选取高斯核函数，根据Silverman法选取窗框，利用局部线性估计方法估计得到时变弹性生产函数模型(11)的时变资本产出弹性α(t)，根据β(t)=1-α(t)得到时变劳动产出弹性(表1)，计算出资本、劳动力、中性技术进步、偏向技术进步、外延和内涵贡献率(表2)，并给出变化趋势图(图1—图3)。
    
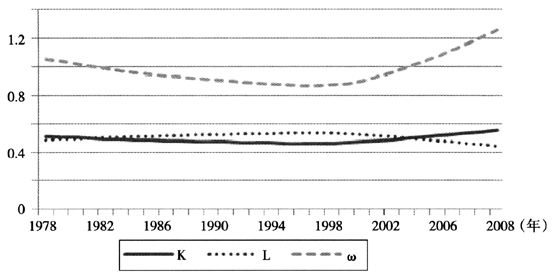
    图1时变弹性与资本密集度
    
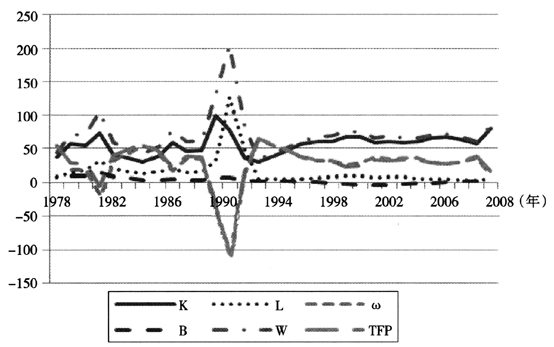
    图2要素贡献率
    
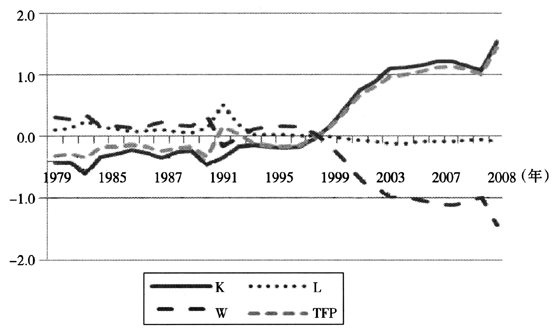
    图3要素贡献率变化
    
    
    
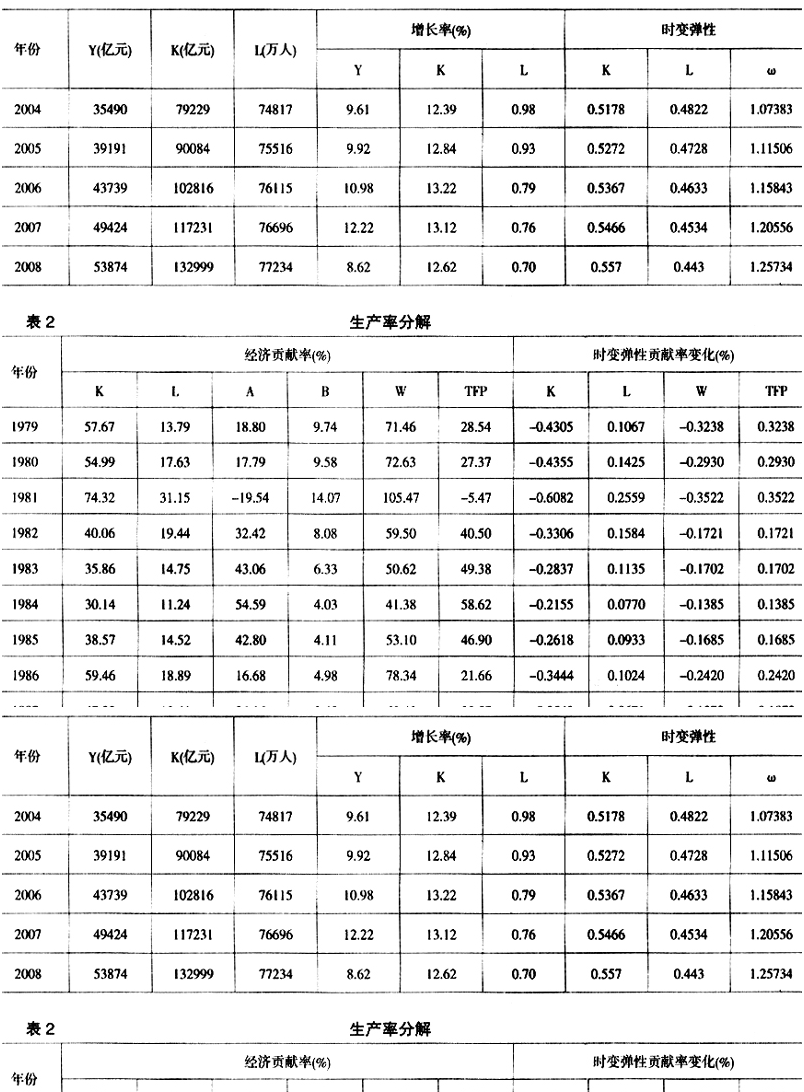
    我国处于经济转型时期，随着生产要素的流动限制减少和价格放开，资本和劳动力的数量与价格是逐期变化的，因而不同时期的资本和劳动力份额也会存在一定程度的变化。由表1和图1可知，在1978-2008年这段时期内，中国资本产出弹性和劳动力产出弹性都不是固定不变的常数，而是随时间变化而呈现出非线性变化特征。资本产出弹性在0.4642～0.5570之间，劳动力产出弹性在0.4430～0.5358之间，相对资本密集度在0.7954～1.1541之间。在1978-2008年期间，资本弹性、劳动力弹性和相对资本密集度可以粗略地划分为两个阶段：(1)在第一阶段1978-1996年，资本弹性从1978年的0.5129逐步下降至1996年的0.4642，劳动力弹性从1978年的0.4871逐步上升至1996年的0.5358，相对资本密集度从1978年的0.9497逐步上升至1996年的1.1541，说明在这段时期发生了劳动偏向型技术进步；(2)在第二阶段1996-2008年，资本弹性从1996年的0.4642快速上升至2008年的0.5570，劳动力弹性从1996年的0.5358快速下降至2008年的0.4430，相对资本密集度从1996年的1.1541快速下降至1996年的0.7954，说明在这段时期发生了资本偏向型技术进步。本文研究结果进一步证实了Shigeru Iwata(2003)、Ahmad(2005)、赵志耘等(2006)、Bing Xu和Berlin Wu(2007)、高宇明和齐中英(2008)、章上峰和许冰(2009，2010)、罗羡华等(2009)、许冰(2010)、章上峰等(2011)、章上峰和顾文涛(2011)等关于产出弹性时变的研究结论。
    由表2和图2可知：(1)从经济增长平均贡献率大小顺序看，依次是资本、中性技术进步、劳动力、和偏向技术进步，分别为57.29％，24.43％，15.58％，2.70％；外延平均贡献率为72.87％，接近四分之三，内涵贡献率仅为27.13％，约为四分之一。以上数据说明中国30年经济增长方式主要表现为粗放型经济增长方式。(2)从1979-2008年要素贡献率变化趋势看，主要可以划分为两个阶段：1992年以前要素贡献率变化幅度较大，这是由于改革开放初期经济增长和资本、劳动力投入数量变化较大引起的。1992年以后，由于资本投入增长速度的不断加快，资本贡献率有逐年上升的趋势，劳动贡献率由于劳动增长速度的放慢而在逐年平稳下降，外延贡献率整体上也是逐年上升；中性技术进步和偏向技术进步贡献率则是逐年下降趋势，虽然2000年以后偏向技术进步贡献率开始上升，但是整体上内涵贡献率呈现逐年下降的趋势。郑玉歆(1999，2007)从全要素生产率的阶段性发展特征对近年来生产率下降趋势给出了一个合理的解释。
    由表2和图3可知，根据时变弹性变化的阶段性，可以将弹性变化导致要素经济增长贡献率变化量粗略地划分为两个阶段：(1)在第一阶段1979-1996年，由于资本弹性逐步下降，劳动力弹性逐步上升，资本贡献率平均减少0.2832，劳动力贡献率平均增加0.1157，外延贡献率平均减少0.1675，内涵贡献率平均增加0.1675。(2)在第二阶段1997-2008年，资本弹性快速上升，劳动力弹性快速下降，资本贡献率平均增加0.9817，劳动力贡献率平均减少-0.0812，外延贡献率平均增加0.9005，内涵贡献率平均减少0.9005。整体上，由于资本增长率大于劳动力增长率，资本弹性变化方向决定了外延贡献率和内涵贡献率变化方向，1979-2008年资本、劳动力、外延和内涵贡献率平均变化量分别为0.22，0.04，0.26和-0.26。时变弹性生产函数生产率分解公式政策含义得到经验研究的有效验证。
    五、研究结论
    我国处于经济转型时期，随着生产要素的流动限制减少和价格放开，资本和劳动力的数量与价格是逐期变化的，因而不同时期的资本和劳动力份额也会存在一定程度的变化。包含中性技术进步假定的传统生产函数模型，难以反映转型时期技术进步偏向引致资本和劳动力产出弹性变化实际以及对经济增长的影响。时变弹性生产函数沿用熟悉的Cobb-Douglas生产函数形式，拓展为变参数Cobb-Douglas生产函数，具有明确的经济学意义。本文基于时变弹性生产函数，推导出经济增长率等于资本、劳动力、中性技术进步和偏向技术进步贡献度之和。全要素生产率增长率，即资本投入和劳动力投入不能解释的“索洛余值”，在数值上等于中性技术进步增长率与偏向技术进步增长率之和，等于产出增长率减去资本投入和劳动力投入增长率的加权和，还等于资本生产率增长率与劳动生产率增长率的加权和，其权数分别为资本产出弹性和劳动时变产出弹性。
    在不变规模报酬假定下，资本产出弹性等于资本收入份额，劳动产出弹性等于劳动收入份额。时变弹性生产函数生产率分解公式，对经济发展方式转变具有重要的政策含义：通常情况下，资本增长率高于劳动增长率，如果提高资本份额、降低劳动份额，即提高资本产出弹性、降低劳动产出弹性，将提高资本贡献率，降低劳动贡献率，提高外延贡献率，降低内涵贡献率，从而导致经济向粗放型发展方式转变，不利于经济可持续增长。反之，如果降低资本份额、提高劳动份额，即降低资本产出弹性、提高劳动产出弹性，将降低资本贡献率，提高劳动贡献率，减少外延贡献率，提高内涵贡献率，从而促进经济向集约型发展方式转变，有利于经济可持续增长。时变弹性生产函数生产率分解公式政策含义得到经验研究的有效验证。我国现在是一个劳动力资源丰富的发展中国家，应该充分利用中国当前劳动力多且相对便宜的优势发展劳动力相对密集的产业，或者在资本密集型产业中劳动力密集的区段，提高初次分配中劳动收入份额，实现我国经济“包容性”增长。
    参考文献：
    [1]曹吉云：《我国总量生产函数与技术进步贡献率》[J]，《数量经济技术经济研究》2007年第11期。
    [2]高宇明、齐中英：《基于时变参数的我国全要素生产率估计》[J]，《数量经济技术经济研究》2008年第2期。
    [3]花俊洲、吴冲锋、梅长林：《一类半参数可变系数广义线性模型及其拟合》[J]，《统计研究》2003年第12期。
    [4]黄勇峰、任若恩、刘晓生：《中国制造业资本存量永续盘存法估计》[J]，《经济学季刊》2002年第2期。
    [5]李子奈、叶阿忠：《高等计量经济学》[M]，清华大学出版社，2004年。
    [6]罗羡华、杨振海、周勇：《时变弹性系数生产函数的非参数估计》[J]，《系统工程理论与实践》2009年第4期。
    [7]许冰：《外国直接投资对区域经济的产出效应——基于路径收敛设计的研究》[J]，《经济研究》2010年第2期。
    [8]章上峰、许冰：《时变弹性生产函数与全要素生产率》[J]，《经济学(季刊)》2009年第2期。
    [9]章上峰、许冰：《初次分配中劳动报酬比重测算方法研究》[J]，《统计研究》2010年第8期。
    [10]章上峰、许冰、顾文涛：《时变弹性生产函数模型统计学与经济学检验》[J]，《统计研究》2011年第6期。
    [11]章上峰、顾文涛：《超越对数生产函数的半参数变系数估计模型》[J]，《统计与信息论坛》2011年第7期。
    [12]张军、吴桂英、张吉鹏：《中国省际物质资本存量估算：1952-2000》[J]，《经济研究》2004年第10期。
    [13]张平：《在增长的迷雾中抉择：行难知亦难》[J]，《经济研究》2006年第2期。
    [14]赵志耘、刘晓路、吕冰洋：《中国要素产出弹性估计》[J]，《经济理论与经济管理》2006年第6期。
    [15]郑玉歆：《全要素生产率的测度及经济增长方式的“阶段性”规律——由东亚经济增长方式的争论谈起》[J]，《经济研究》1999年第5期。
    [16]郑玉歆：《全要素生产率的再认识——用TFP分析经济增长质量存在的若干局限》[J]，《数量经济技术经济研究》2007年第9期。
    [17]Ahmad, I., Leelahanon, S., and Li, Q., 2005, Efficient Estimation of a Semiparametric Partially Linear Varying Coefficient Model[J], The Annals of Statistics, 33(1), 258～283.
    [18]Bing Xu, Berlin Wu, 2007, On Nonparametric Estimation for the Growth of Total Factor Productivity: A Study on China and Its Four Eastern Provinces[J], International Journal of Innovative Computing, Information and Control, 3(1), 141～150.
    [19]Bentolina, S. and Saint-Paul, G., 2003, Explaining Movements in the Labor Share[J], Contributions to Macroeconomics, 3(1).
    [20]Blanchard, O. J., 1997, The Medium Run[R], Brookings Papers on Economic Activity, 1997(2), 89～158.
    [21]Jones, C. I. and Romer, P. M., 2010, The New Kaldor Facts: Ideas, Institutions, Population, and Human Capital[J], American Economic Journal: Macroeconomics, 2(1), 224～245.
    [22]Jianqing Fan and Tao Huang, 2005, Profile Likelihood Inferences on Semiparametric Varying-coefficient Partially Linear Models[J], Bernoulli, 11(6), 1031～1057.
    [23]Gollin, D., Williams, C., 2002, Getting Income Shares Right[J], Journal of Political Economy, 110(2), 458～474.
    [24]Hicks, J. R., The Theory of Wages[M], MacMillan, London, 1932.
    [25]Hofman, Antre, A., 2001, Economic Growth, Factor Shares and Income Distribution in Latin American in the Twentieth Century[R], Presented at the International Workshop on "Modern Economic Growth and Distribution in Asia, Latin America, and the European Periphery: A Historical National Accounts Approach", March: Tokyo, 16～18.
    [26]Kaldor, N., 1961, Capital Accumulation and Economic Growth[M], Cambridge: MacMillan.
    [27]Leandro Prados de la Escosura and Joan R. Rosés, 2003, Wages and Labor Income in History: A Survey[R], Working Paper 03-10, Economic History and Institutions Series 06, February.
    [28]Robert E. Lucas, Jr., 1988, On the Mechanics of Economic Development[J], Journal of Monetary Economics, 22(1): 3～42.
    [29]Poterba, J. M., 1998, The Rate of Return to Corporate Capital and Factor Shares: New Estimates Using Revisited National Income Accounts and Capital Stock Data[R], NBER Working Paper No. 6263, Carnegie-Rochester Conference Series on Public Policy 48, 1998, 211～246
    [30]Romer, P. M., 1986, Increasing Returns and Long Run Growth[J], Journal of Political Economy, 94(5), 1002～1037.
    [31]Romer, P. M., 1990, Endogenous Technology Change[J], Journal of Political Economy, 98, S71～S102.
    [32]Shigeru Iwata, Mohsin S. Khan and Hiroshi Murao, 2003, Sources of Economic Growth in East Asia: A Nonparametric Assessment[R], IMF Staff Papers, 50(2), 157～177.
    [33]Solow, R. W., 1957, Technical Change and the Aggregate Production Function[R], Review of Economics of Statistics, 39(3), 312～320.
    [34]Solow, R. M., 1958, A Skeptical Note on the Constancy of Relative Shares[R], American Economic Review, 48(4), 618～631.
    [35]Solow, R. M., 1956, A Contribution to the Theory of Economic Growth[J], Quarterly Journal of Economics, 70(1), 65～94.^