家族企业的高管激励与研发投入关系研究——基于家族所有权和控制权视角

    三、变量设计与模型构建
    1.变量设计
    (1)被解释变量
    研发投入强度(R&D)。国内外现有研究中关于研发投入的度量主要采用三种方式：研发投入/总资产、研发投入/营业收入和研发投入/市场价值。由于本文搜集的研发投入数据主要来自于报表附注中支付的其他与经营活动有关的现金项目，反映的是企业当年研发投入的流量数据，为了对应及排除企业规模的影响，用研发强度(研发投入/营业收入)来衡量企业的研发投入。
    (2)解释变量
    高管股权激励(MSR)。鉴于我国上市公司董事在公司内部决策等方面所起的重要作用，本文高管股权激励以实施股权激励的公司高管与董事持股数量占当年公司总股数的比值来衡量，用MSR表示。
    高管薪酬激励(SAL)。选取上市公司董事前三名与高管前三名现金薪酬总额的自然对数作为高管薪酬激励的代理变量，用SAL表示。
    (3)调节变量
    家族所有权(FAM_OWN)。本文采用现金流权测量家族所有权，即家族以一致行动、金字塔持股、交叉持股等直接或间接持股方式获取的终极所有权比例，用FAM_OWN表示。
    家族控制权(FAM_CON)。本文借鉴贺小刚、连燕玲(2009)关于家族控制的研究，采用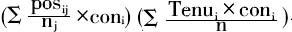作为代理变量，用FAM_CON表示。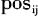为家族成员i所控制的第j类职位所对应的职位等级系数③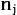；为家族企业中第j类职位的任职人数；为家族成员i所对应的亲缘指数④；为家族成员i在其职位上的任职期限；n为在高层任职的家族成员的总人数。
    (4)控制变量
    公司规模(SIZE)，用企业总资产的自然对数来表示；企业绩效(ROA)，用总资产收益率表示；资本结构(LEV)，用资产负债率表示；行业哑变量(IND)，用来进行样本企业的行业分类，分为高研发企业和低研发企业，若为高研发企业，则赋值为1，否则为0；年度哑变量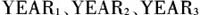，以2010年为基准，若为2011年，则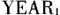赋值为1，否则为0；若为2012年，则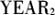赋值为1，否则为0；若为2013年，则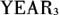赋值为1，否则为0。
    2.模型构建
    通过逐步多元回归分析，本文构建了以下6个模型，以检验家族所有权与控制权对于高管薪酬与研发投入关系的调节效应。
    
    模型(1)在考虑所有控制变量的基础上，探讨高管激励(高管股权激励和高管薪酬激励)与研发投入的关系，以验证假设1和假设2。模型(2)在模型(1)的基础上增加了家族所有权与控制权两个调节变量，为后面的交互效应模型提供对比。模型(3)在模型(2)的基础上加入了高管股权激励(MSR)与家族所有权(FAM_OWN)的交互项(MSR×FAM_OWN)，以验证假设3。同理，模型(4)在模型(2)的基础上加入高管薪酬激励(SAL)与家族所有权(FAM_OWN)的交互项(SAL×FAM_OWN)，以验证假设4；模型(5)在模型(2)的基础上加入了高管股权激励(MSR)与家族控制权(FAM_CON)的交互项(MSR×FAM_CON)，以验证假设5。模型(6)在模型(2)的基础上加入了高管薪酬激励(SAL)与家族控制权(FAM_CON)的交互项(SAL×FAM_CON)，以验证假设6。若交互项显著，说明家族所有权与控制权对高管激励与研发投入关系有调节作用。
    

上一页  [1] [2] [3] [4] [5] [6] [7] 下一页