再看另一个股票过去一年的收市分布图(见图 3)。
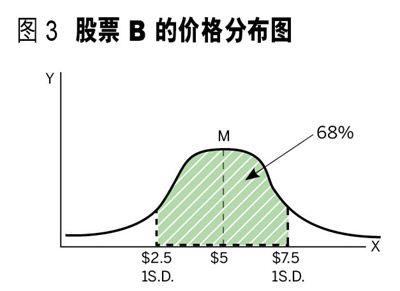
股票 B 的中间值是 5 元,假设一个标准差是 50%。根据这只股票 B 的分布图和标准差,可以得出以下推论:股票 B 在未来一年之内的上下波幅不超过 50% 的机会是 68%。
股票 A 的一个标准差是 20%,股票 B的一个标准差是 50%,股票 B 的风险比股票 A 的风险大 2.5 倍。如果一名投资者投资股票 B 的话,他的期望回报便应该比股票 A 大 2.5 倍。也可以说,如果股票 A 和股票 B 的回报大致一样的话,投资者应投资股票 A,而放弃股票 B。
当然,本文只是简短的介绍,内容可能过于简单。正像纳西姆·尼古拉斯·塔勒布(Nassim Nicholas Taleb)在其名著《黑天鹅》中解释的那样,这种对风险的量化分析,忽视了所谓的“黑天鹅”事件─这种事件完全无法预测,具有重大影响,通过“事后的知识”可以解释。因此,用这些观点作为唯一的风险衡量标准,会使投资者很容易受到不可预测的金融冲击的影响。全球各主要银行风险管理系统的崩溃,证明了塔勒布理论的正确性。但这并不能推翻使用现代投资组合理论的可行性。我们只是需要使用更多的方法,如压力测试等,来更有效地衡量风险。
分散投资的好处
利用标准差的方法,我们可以计算出每一只股票或债券的风险。当一名投资者买入一只股票的时候,他对此股票的回报率便有期望,同时他也可根据以往的数据计算出此股票的预期风险,即标准差。例如,投资者对股票 C 的期望回报率是 11%,标准差是 15%,即代表此股票的回报率有 68% 的机会在 -4%(11%-15%)和 26%(11%+15%)之间。
但投资者的投资组合往往不只一只股票。若他同时考虑买入股票 D,假如股票 D 的期望回报是 25%,标准差是 20%,他可考虑将 100% 的资金投资在股票 C 或股票 D,也可将资金投资在股票 C 和股票 D 的不同组合。如果投资组合内包含股票 C 和股票 D 的话,便需要计算出投资组合的预期回报和标准差。
计算投资组合的预期回报比较简单,就是股票 C 和 D 的个别预期回报率的加权平均数。例如,组合中股票 C 占 80%,股票 D 占 20%,此投资组合的预期回报便是 13.8%(11% x 0.8 + 25% x 0.2=13.8%)。
但此投资组合的标准差却不是股票 C 和股票 D 的个别标准差的加权平均数,除非两者的股价波动的步伐完全一致。在这样的情况下,他们的相关系数便是 1,即两只股票的波动完全一样。但我们知道,绝大多数股票的波动都并不完全一致,同一产业的股票波幅会比较接近,它们之间的相关系数会比较接近 1;但有一些股票的走势可能会很少关联,例如公用股和银行股的价格表现会较为独立;若是这样的情况,它们之间的相关系数便会相差较大。计算出一个投资组合的标准差比较复杂,因此并不打算在这里介绍。只需记住:只要股票之间的相关系数小于 1,投资组合的标准差会小于个别股票标准差的加权平均数。表 1 列出了假如股票 C 和股票 D 的相关系数为 0.3 的情况下,股票 C 和股票 D 几个不同组合的预期回报率和标准差。
按股票 C 和股票 D 的不同组合而得出的预期回报和标准差,我们可以画出图 4。
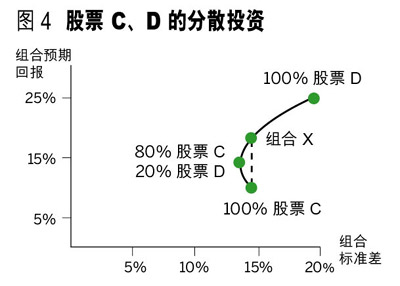
在这里,我们可以看到,若投资组合完全是股票 C 的话,这个组合的预期回报和标准差便完全与股票 C 一样,即 11% 和 15%。但是,组合 X 的风险和股票 C 一样,标准差都是 15%,但预期回报较高。很明显,投资者不应只投资在股票 C,而应分散投资股票 D,以建立投资组合 X。理由很简单,风险没有增加,但回报却增加了。

以上是分散投资的理论根据。在每一个特定的风险情形下,我们都可以在特定的投资范围内选择不同比例的投资类别,使这个投资组合的预期回报达到最高。
