作者:置盐信雄(NobuoOkishio)
骆桢、李怡乐译孟捷校
载《教学与研究》2010年第7期
一
本文将考察马克思的利润率趋向下降的规律①,在《资本论》第三卷中马克思将此命题表述如下:
1.资本家之间的竞争迫使他们引进新的生产技术以提高劳动生产率。
2.提高劳动生产率的生产技术通常会提高“资本有机构成”。资本有机构成由c/v来度量,其中v、c分别为可变资本和不变资本。
3.利润率为m/(c+v),其中m表示“剩余价值”。于是,如果剩余价值率m/v保持不变,随着资本有机构成c/v的提高,利润率下降。
4.如果实际工资率不变,提高工资品行业及其相关行业劳动生产率的生产技术会提高剩余价值率。这个效应阻碍了利润率的下降,但作用有限。
5.于是,尽管有这些起阻碍作用的因素,由于提高资本有机构成的新技术的不断引入,利润率有下降的趋势。
针对这些命题,有以下疑问:
1.资本家引入的新的生产技术真的必然提高劳动生产率吗?
2.提高劳动生产率的生产技术通常会提高资本的有机构成吗?
3.新生产技术对利润率有着对立的双重影响:增加剩余价值率以及提高资本有机构成。然而为什么利润率有下降趋势呢?
我们将依次考察这些问题。
————————————————————
①此处原文为德文———译者注。下文观点见于一些不太引人注意的文章,KeiShibata:“On the Law of Decline in the Rate of Profit,”Kyoto University Economic Review,July,1934,以及“On the General ProfitRate,”ibid.,January,1939.
————————————————————
二
资本家是否引入一项新技术并不取决于其是否能提高劳动生产率,而是取决于其能否降低生产成本。“生产率准则”不同于“成本准则”。
第i种商品的劳动生产率由1/ti度量,其中ti表示生产一单位第i种商品所耗费的直接或间接的必要劳动量。ti由下列方程决定
ti=∑aijtj+τi(i=1,2,…,n)(1)
其中aij表示生产一单位第i种商品所必需的第j种商品的直接投入量,而τi表示生产一单位第i种商品所需要的直接劳动量。
在第k产业中,新技术能提高生产第k种商品的劳动生产率的条件是
∑akjtj+τk>∑a′kjtj+τ′k (2)
其中(a′k1,a′k2,…,a′kn,τ′k)表示第k产业中的新技术①,条件(2)是“生产率准则”。
另一方面,“成本准则”是
Σakjqj+τk>Σa′kjqj+τ′k(3)
其中qj=pj/w,pj和w分别表示第j种商品的价格和货币工资率。
只有对所有的i而言qi=ti时,“生产率准则”(2)和“成本准则”(3)才等价。而在资本主义经济中对于所有的i都有qi>ti,因为每个行业都必须存在正的利润,从而必须满足下列不等式:
qi>Σaijqj+τi (i=1,2,…,n)(4)
比较(1)和(4),我们可得,对所有的i有qi>ti。②
————————————————————
①参见文章末数学附录Ⅰ。
②参见文章末数学附录Ⅱ。
————————————————————
因此,“生产率准则”不同于“成本准则”,由于资本家采用的是“成本准则”而不是“生产率准则”,从而资本家所引入的新技术虽必须降低生产成本,却不必然提高劳动生产率。这是资本主义经济阻碍生产力进步的一种表述。
三
提高劳动生产率的生产技术是否会提高资本有机构成,在没有统计研究的情况下是无法回答这一问题的,因此本文对此将不作讨论。
在马克思的视角中,为了提高劳动生产率,生产的迂回程度必然增加。于是生产商品所耗费的必要劳动量相对于生产必需的生产资料所耗费的劳动量减少。
马克思用ci/vi来度量第i产业的资本有机构成。但这种度量不能充分展示马克思的视角。
用我们的记法
ci=Σaijtj
vi=τiΣbjtj
其中(b1,b2,…,bn)表示劳动者付出一单位劳动所换得的一揽子消费品,称为实际工资率。从而一个行业的资本有机构成取决于两个因素:决定aij,τi和ti的生产技术,以及决定bi的真实工资率。即使生产技术不变,真实工资率的变动也会引起资本有机构成的变化。
为清晰地展示马克思的视角,我们认为最好采用Σaijtj/τi来度量有机构成,而不是ci/vi=Σaijtj/τiΣbjtj。我们度量的Σaijtj/τi或者ci/(vi+mi)取决于生产技术并且清楚地表示出直接劳动和生产资料所包含的间接必要劳动之间的比例。我们将ci/(vi+mi))称为第i产业的“生产的有机构成”。
四
剩余价值率m/v,用我们的符号表示如下:
m/v=τi-τiΣbjtj/τiΣbjtj=1-Σbjtj/Σbjtj(5)
由上述方程可知,剩余价值率取决于真实工资率和工资品的劳动生产率。如果bj>0,则第j产业是工资品行业。工资品的劳动生产率不仅取决于工资品行业本身的生产技术,还取决于与工资品行业不可分①的产业的技术。因为,由方程(1)所示,ti不仅取决于第i产业本身的生产技术,同时还取决于作为第i产业直接或间接投入品的产业的技术。由此我们将所有工资品行业和与工资品行业不可分的行业称为“基本品行业”。于是,给定真实工资率,剩余价值率仅取决于“基本品行业”的生产技术。
如果在某一“基本品行业”引入新的生产技术,并且导致某些工资品的劳动生产率提高,即对于bi>0的ti变小,于是,给定真实工资率,剩余价值率必然增加。但是非基本品行业的生产技术变化不影响剩余价值率。
在分析对剩余价值率的影响时,区分“基本品行业”和“非基本品行业”是很重要的。这一点马克思和李嘉图都充分认识到了②。但这个区分在分析技术变革对利润率的影响时也是至关重要的。李嘉图坚持了这一点,而马克思否认了这个观点。这也就是我们后面将要说的马克思的错误。

————————————————————
①与投入-产出理论中系数矩阵的不可分解(indecomposable)概念对应。———译者注
②“购买这类必需品,既须增加支出,劳动者自然会要求增加工资。工资增加,必致减低利润。至若非必要品如绢物天鹅绒家具等,则虽因所费劳动增加而价格腾贵,亦决不能影响利润。只有工资腾贵可影响利润;劳动者既不消费绢物天鹅绒,故不能提高工资。”(D.Ricardo:Principles,p.118,Works,ed.byP.Sraffa)参见李嘉图:《经济学及赋税之原理》,郭大力,王亚南译,第63页,上海,上海三联书店,2008———译者注。
“要使劳动力的价值降低,生产力的提高必须扩展到这样一些产业部门,这些部门的产品决定劳动力的价值,就是说,它们或者属于日常生活资料的范围,或者能够代替这些生活资料。但是,商品的价值不仅取决于使商品取得最终形式的那种劳动的量,而且还取决于该商品生产资料所包含的劳动量。例如,皮靴的价值不仅取决于鞋匠的劳动,而且还取决于皮革、蜡、线等等的价值。因此,那些为生产必要生活资料提供不变资本物质要素(劳动资料和劳动材料)的产业部门中生产力的提高,以及它们的商品相应的便宜,也会降低劳动力的价值。相反,那些既不提供必要生产资料、也不为制造必要生活资料提供生产资料的生产部门中的生产力的提高,不会影响劳动力的价值。”(K.Marx:DasKapital,ErstweBd.BesorgtνomMarx-Engels-Lenin-Institut,Moskau,S.330.)参见马克思:《资本论》,第2版,第1卷,第366-367页(第十章《相对剩余价值的概念》),北京,人民出版社,2004———译者注。
————————————————————
五
在“基本品行业”新引进的马克思式的生产技术有两种效应:提高剩余价值率以及资本有机构成。但是马克思坚持利润率有下降的趋势。为什么前一个影响不能完全抵消后者呢?
对此,大多数的结论和通常的回答如下:利润率m/(c+v),不能超过生产有机构成的倒数,即m/(c+v)≤(v+m)/c(6)
只有当v=0时,上式才能取等号,换句话说,此时工人免费劳动。这一毫无疑问的关系式表明生产有机构成的倒数是利润率的上限。并且,根据马克思的观点,这个上限是时间的减函数,从而(v+m)/c→0。因此,即使高剩余价值率出现,利润率仍不能超越其上限,并且这个上限本身是随时间递减的。由此,虽然利润率会上下波动,如图1所示,其趋势不可能上升或者保持不变。
上述推理在逻辑上似乎没有什么问题。如果我们接受马克思关于生产的有机构成的观点,则这个结论似乎是必然的。甚至那些在严格意义上否认马克思观点的人也不能否认生产的有机构成具有上升的趋势,即使不是一直上升。并且上述证明仅需要上升的趋势,而不需要严格递增。
不幸的是上述表象只是误导,我们下面将进一步分析。
六
第一个问题是关于不等式(6)本身的,这个不等式是否合理?如果利润率能通过m/(c+v)来计算,则(6)式必然成立。马克思通过总资本以价值形式瓜分总剩余价值来计算一般利润率,即m/(c+v)。但是这个方法并不正确。一般利润率r是由下列方程决定的:
qi=(1+r)(Σaijqj+τi) (I=1,2,…,n)
1=Σbiqi(7)
初看上去,这样得到的r总体上并不等于m/(c+v)。这样的一般利润率r,其上限是否由生产的有机构成决定呢?答案是肯定的。我们可由方程(1)和(7)得以下不等式①:
r<τi/Σaijtj(8)
对于某些i而言(8)式的右边就是第i行业的生产有机构成的倒数。从而,不等式(8)表明一般利润率不能超过某些行业生产有机构成的倒数。这样的关系与不等式(6)有着相同的作用。因为根据马克思的观点,所有行业的生产有机构成都有无限升高的趋势,于是一般利润率在长期中必然下降。
因此,虽然不等式(6)不正确,但是由不等式(6)所得结论的合理性由于不等式(8)而依旧成立。这样一来,我们能否同意马克思的命题呢?在此之前我们需要做更多的工作。
七
下一个所要考察的问题是关于资本家新引进的生产技术的类型。马克思认为资本家迫于竞争的压力会引进提高劳动生产率并提高生产有机构成的新技术,并且在长期,所有行业的生产有机构成无限制的提高导致了利润率的下降。
但是,如前所述,在资本主义经济中资本家选择新的生产技术首先要遵循成本准则。即使存在能大幅提高劳动生产率的技术,也不会被资本家引进,除非其能降低生产成本,这个条件为劳动生产率的提高设置了限制。
我们必须考察遵循“成本准则”所引入的生产技术对一般利润率的影响。一般利润率由方程(7)决定。假设在第k行业中的生产技术(ak1,…,akn,τk)被新技术(a′k1,…,a′kn,τ′k)取代,且满足不等式(3)。方程(7)中的一般利润率r如何变动呢?我们有以下结论,其证明在附录Ⅳ和Ⅴ中给出:
(1)如果引入新技术的行业是“非基本品行业”,则一般利润率不会受影响。
(2)如果引入新技术的行业是“基本品行业”,则一般利润率必然上升。
非基本品行业的生产技术不影响一般利润率的命题为李嘉图所揭示,却被马克思拒绝②。马克思之所以不能得出正确结论的原因在于其通过包含非基本品行业的总资本瓜分总剩余价值,即m/(c+v)来计算一般利润率。如果一般利润率是m/(c+v)的话,则非基本品行业扮演着与基本品行业相同的角色,其区别在分析对一般利润率影响的时候变得无足轻重。但是一般利润率不能由如此简单的商数来计算,而应由方程(7)计算,在那里非基本品行业只起消极的作用。
基本品行业中满足“成本准则”(3)的新技术的引进必然提高一般利润率这个命题与马克思利润率下降规律不相容。这个命题表明,只要新技术引进满足成本准则并且实际工资保持不变的话,无论生产有机构成会提高多少,一般利润率会无一例外地上涨。而且我们可以有把握地说,以原有的价格和工资计算,资本家引进的每一项技术都是降低成本的。从而,我们必须接受:资本家在基本品行业采纳的每一项技术创新必然提高一般利润率,除非实际工资上涨得足够高。
————————————————————
①参见文章末数学附录Ⅲ。
②“设若自种谷物,自制衣服,自造必需品的价格,不能减低,但若能以较廉价格得之于新市场,工资亦将低落,同时,利润亦将提高。但是,由外国贸易扩张或机械改良而得之物,若纯由富有者消费,利润率自然不会发生什么变动。葡萄酒、天鹅绒、丝绢,以及其他昂贵物品,即令价格低落了百分之五十,工资率亦不受到影响,因之,利润率依然不变。”———D.Ricard:op.cit.,p.132,参见李嘉图:《经济学及赋税之原理》,郭大力,王亚南译,第73页,上海,上海三联书店,2008———译者注。
对此,马克思反驳道:“我们看到,整个这一段都写得极为草率。但是,撇开这些形式上的缺点不谈,这一切,就像在整个关于相对剩余价值的这种研究中一样,只有在把“利润率”读成“剩余价值率”的情况下才是正确的。即使对奢侈品来说,上述改良也可以提高一般利润率,因为这些生产领域的利润率,同其他一切生产领域的利润率一样,也参加一切特殊利润率平均化为平均利润率的过程。”(K.Marx:TheorienǔberdenMehrwert,ZweiterBand,ErsterTeil,herausgegebenvonKarlKautsky,S.147)参见《马克思恩格斯全集》,中文1版,第26卷第II册,第481页,北京,人民出版社,1963———译者注。
————————————————————
八
既然附录已经给出了这两个命题完整的一般性证明,我们这里就用一个简单的数值例子进行说明。
假设有产业Ⅰ生产生产资料,产业Ⅱ生产工资品,产业Ⅲ生产奢侈品,并且这些产业的生产技术如下表:
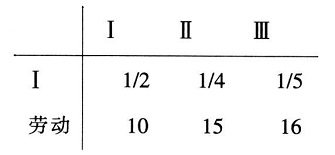
这个表格显示,比如,第二产业生产一单位工资品必须投入1/4单位的生产资料和15单位的直接劳动。
接下来,令实际工资率为1/45单位工资品。
于是,一般利润率r由下列方程决定:
q1=(1+r)(1/2q1+10)(9.1)
q2=(1+r)(1/4q1+15)(9.2)
q3=(1+r)(1/5q1+16)(9.3)
1=q2/45(9.4)
我们很容易解得r=50%,q1=60,q2=45,q3=42, 其中qi=pi/w。
现在,我们假设技术变革发生在非基本品行业。在这个例子中第三个行业是非基本品行业,而其他两个则是基本品行业,因为第三行业对于维持其他行业的生产并不是必需的,而第一、第二行业对所有行业而言则是必需的。观察上述四个方程,我们会发现方程(9.3)的不同之处。(9.1)(9.2)和(9.4)可以离开(9.3)独立决定r、q1和q2,同时(9.3)用已经求出来的r、q1的值来决定q3。从而(9.3)不以任何方式参与决定一般利润率。因此非基本品行业的任何技术变革,即改变方程(9.3)的参数,不会对一般利润率产生任何影响。这就是前一部分提出来的第一个命题:非基本品行业不能参与一般利润率的决定,而只能被动接受由基本品行业决定的一般利润率。
但是,这并不是说非基本品行业的生产技术与一般利润率一点关系都没有,比如说我们将(9.3)换为:q3=(1+r)(1/20q1+3/4q3+6)(9.3′)
并且同前面一样q1=60, r=50%,我们得到值为负的q3。这意味着如果在第三产业的技术要求生产一单位第三类商品需要投入1/20单位的第一类商品和3/4单位的第三类商品,以及6单位劳动,则各行业间的一般利润率不存在。所以,虽然非基本品行业的生产技术不影响一般利润率的高低,但是却与一般利润率水平本身是否存在有关。
接下来我们假设技术变革发生在基本品行业,比如第二产业,我们假设第二个行业中的资本家采用“马克思”式的新技术,即能提高劳动生产率及生产的有机构成,并且按原有价格和工资计算成本是降低的。
作为数值例子,我们假设第二行业技术被替换为
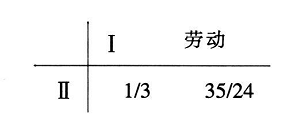
这个新技术是“马克思”式的。首先,与旧技术相比,其提高了劳动生产率。在原有技术下劳动生产率由ti衡量,并由下式决定:
t1=1/2t1+10(10.1)
t2=1/4t1+15(10.2)
从而t1=20 t2=20。与此对应,在新技术下(10.2)被替换为
t2=1/3t1+35/24(10.2′)
为了生产一单位工资品所必需的劳动t2减少得很多,从20个单位到8.125个单位。
其次,生产有机构成上升。原有技术下有机构成为1/4t1/15=1/3,但新构成为1/3t1/35/24=32/7。第二产业的有机构成有巨大的上升。
最后,依照旧技术下确定的价格和工资计,作为工资单位的第二种商品的生产成本比旧技术下更低。在旧技术下第二种商品的成本是1/4q1+15=30,而在新技术下成本为1/3q1+35/24=21.5。
通过把(9.2)替换为下式,我们可以得到其对一般利润率的影响。
q2=(1+r)(1/3q1+35/24)(9.2′)
方程(9.1)(9.2′)和(9.4)的解为:q1=80,q2=45,r=60%,一般利润率上升。
九
我们的结论与马克思的利润率趋向下降的规律相反,除非实际工资率有足够高的上升,否则资本家引进的技术创新不会降低一般利润率。基本品行业的技术创新会提高一般利润率,而非基本品行业的创新对一般利润率水平没有影响。
在我们看来,马克思之所以不能得出正确的结论,有两个原因,一是他对所谓“转形问题”的研究不够彻底,二是他忽略了在引进新技术方面资本主义行为的重要特征。
第一点关系到马克思的方程:
一般利润率=m/(c+v)以及由此而来的在分析一般利润率时对基本品和非基本品行业之间区别的忽视。马克思意识到自己对生产价格的分析还不够充分①,但他没有能够反思自己的分析。
关于第二点,我们不能说马克思不知道这个特征。因为在他的《资本论》中他反复阐述了生产方法选择的资本主义局限性特征②。然而很不幸的是他在思考一般利润率时,却没有考虑这个特征。
在本文末尾,我们简要说明本文对整个马克思主义经济学的意义:
1.利润率趋向下降的规律并不是马克思体系大厦赖以存在的基石。某些人试图从规律中演绎出危机理论,但这样的努力注定将失败。
2.基本品和非基本品行业对一般利润率的不同影响是马克思基础信条的一种表述,即利润是剩余价值的一种表现形式。因为剩余价值率仅仅依赖于基本品行业,而不包括非基本品行业。
3.资本主义采纳技术的特征也是马克思基本命题的一种表述,即资本主义社会的生产关系已成为人类生产力进步的障碍。
4.马克思通过规律想表述的内容是,在资本主义社会中生产力进步不可避免地采取了令人生畏的形式,或称利润率下降。但是如前所述,只要劳动者增加工资的努力失败,资产阶级是能提高利润率的。从而利润率的运动由阶级斗争所决定。
————————————————————
①“当然,以上所说,对商品成本价格的规定是一种修正。我们原先假定,一个商品的成本价格,等于该商品生产中所消费的各种商品的价值。但一个商品的生产价格,对它的买者来说,就是它的成本价格,因而可以作为成本价格加入另一个商品的价格形成。因为生产价格可以偏离商品的价值,所以,一个商品的包含另一个商品的这个生产价格在内的成本价格,也可以高于或低于它的总价值中由加到它里面的生产资料的价值构成的部分。必须记住成本价格这个修正了的意义,因此,必须记住,如果在一个特殊生产部门把商品的成本价格看作和该商品生产中所消费的生产资料的价值相等,那就总可能有误差。”(K.Marx:DasKapital,Bd.Ⅲ,S.189-190)参见马克思:《资本论》,第2版,第3卷,第184-185页(第九章),北京,人民出版社,2004———译者注。
②“如果只把机器看作使产品便宜的手段,那么使用机器的界限就在于:生产及其所费的劳动要少于使用机器所替代的劳动。可是对于资本来说,这个界限表现得更为狭窄。因为资本支付的不是所使用的劳动,而是所使用的劳动力的价值,所以,对资本来说,只有机器的价值和它所替代的劳动力的价值之间存在差额的情况下,机器才会被使用。”“因此,在共产主义社会,机器的使用范围将和在资产阶级社会完全不同。”(K.Marx:op.cit.,Bd.Ⅰ,S.411)参见马克思:《资本论》,第2版,第1卷,第451页(第十三章《机器和大工业》),北京,人民出版社,2004———译者注。
————————————————————
数学附录
Ⅰ
在第k行业中新生产技术能降低生产一单位第k种产品所必需的直接或间接劳动量的条件为
Σakjtj+τk>Σa′kjtj+τ′k(11)
其中(ak1,…,akn,τk)和(a′k1,…,a′kn,τ′k)分别为
第k行业旧的和新的技术,并且ti由下式决定
ti=Σaijtj+τi (i=1,2,…,n)(12)
证明:
如果新技术被引进到第k行业,则新的ti由
下式决定
tk=Σa′kjtj+τ′k
(13)
令(12)的解为(t1,…,tn)同时(13)的解为
(t′1,…,t′n)。由(12)(13)我们得
Δtk=Σa′kjΔtj+(ΣΔakjtj+Δτk)
(14)
其中Δti=t′i-ti, Δakj=a′kj-akj,Δτk=τ′k-τk
方程(13)若要有经济意义的解,即对所有i而言都有ti>0,则其中t的系数必须遵循“霍金斯—西蒙(Hawkins-Simon)条件”①。从而,在(14)中如果ΣΔakjtj+Δτk≥0,则对于所有的i而言Δti≥0。
若ΣΔakjtj+Δτk<0,则对于所有i有Δti≤0,其中Δtk<0。
Ⅱ
如果(q1,q2,…,qn)满足下列不等式
qi>Σaijqj+τi (i=1,2,…,n)(15)
则必满足下列不等式
qi>ti (i=1,2,…,n)(16)
其中,ti由(12)决定。
证明:
由(12)和(15)我们得qi-ti>Σaij(qj-tj) (i=1,2,…,n)
(17)
由(12)中ti的系数必须满足Hawkins-Simon条件,可得关系(16)。
Ⅲ
一般利润率r,由下述方程决定:
1=Σbiqi
(18)
则必然满足关系
r<τi/Σaijtj 对于某些i而言(19)
其中ti由(12)决定并且对于所有i有Σaijtj>0。
证明:
由(18)我们可得
r=qi/Σaijqj+τi-1 对于所有i而言
(20)
对于所有的i,令qi=λiti,并替换qi,同时考虑到τi>0我们得
r<λi/λi*ti/Σaijtj-1 对于所有i而言
(21)①
其中λi*=Σaijλjtj/Σaijtj(22)
λi*是λ1,λ2,…,λn各自以ai1t1,ai2t2,…,aintn为权重的加权平均。所以对于某些i而言必然满足下列关系
λi≥λi*(23)
对于这样的i,我们由(21)和(12)可得
r<ti/Σaijtj-1=τi/Σaijtj(24)
Ⅳ
非基本品行业的技术变革不会影响由(18)决定的一般利润率水平。
证明:
根据定义,非基本品行业的产品不是工资品,因此在方程(18)中bl=0,其中l表示非基本品行业的编号。再一次根据定义,非基本品行业的产品不会成为工资品行业或者生产工资品直接、间接需要的行业的投入品。因此,如果用1到m表示工资品行业以及工资品生产中所必需的行业,则有ail=0(i=1,2,…,m)(25)
其中l表示非基本品行业的编号。从而我们可以挑选出m+1个方程:
1=Σbiqi
(26)
并且他们足以决定一般利润率。因此,非基本品的技术变革不能影响已经被决定了的利润率r。
Ⅴ
如果在第k行业,假设其为基本品行业,引入的新技术满足
Σakjqj+τk>Σa′kjqj+τ′k(27)
则由(26)决定的一般利润率必然上升。
证明:
令β=1/(1+r),(26)可以被重新写成
βqi=Σaijqj+τi (i=1,2,…,m)(28)
1=Σbiqi(29)
在新技术下,一般利润率由(29)以及下式
决定
βqi=Σaijqj+τi (i=1,…,k-1,k+1,…,m)(30)
βqk=Σa′kjqj+τ′k(31)
令(28)和(29)的解为(β,q1,…,qn),而(30)(31)和(29)的解为(β′,q′1,…,q′n)。则由(28)-(31),我们可得
β′Δqi=ΣaijΔqj-qiΔβ (i=1,…,k-1,k+1,…,m)(32)
(33)
0=ΣbiΔqi(34)
其中Δqt=q′t-qt,Δβ=β′-β,Δakj=a′kj-akj以及Δτk=τ′k-τk。由于对于所有i而言q′i>0,因此(32)和(33)中Δq的系数满足Hawkins-Simon条件。同时,由(27)可知(33)式右端第三项为负。因此,如果Δβ≥0,则(32)(33)中的Δqk<0,并且当i≠k时Δqi≤0。由于第k行业是基本品行业,那么至少有一个工资品行业的Δqi<0。但是这与(34)矛盾,因此,我们有Δβ<0,或者说r′>r。Hawkins-Simon定理说明(译者)
该问题涉及线性方程组Bx=c什么条件下具有有经济意义的解,即解大于等于0。
Hawkins和Simon是在以下条件下考察这个问题的:
(1)bii>0;bij<0,i≠j;i,j=1,…,n
(2)c>0
后来由二阶堂(Nikaido)给出了广义Hawkins-Simon定理的证明。
Hawkins-Simon定理:考虑方程Bx=c,其中对于所有i≠j,都有bij≤0。则下列条件是等价的:
(1)给定c>0,则x≥0;
(2)给定c≥0,则x≥0;
(3)矩阵B的左上主子式为正;
(4)矩阵B为P阵(即B的所有主子式为正)。
——以上内容参见WoodsJ.E.:MathematicalEconomics,1978,LongmanInc.,NewYork,p6-7.
[责任编辑陈翔云]
