会员登录
会员注册1.变量选择与描述
(1)制度指标的构建方法——熵值法。在建立一个综合指标体系的过程中，首先需要确定指标体系中各指标的权重，普遍采取的方法有主观赋权法和客观赋权法。主观赋权法是指根据主观的重视程度来决定各指标权重的方法，如“Delphi法、AHP法”；客观赋值法是源于客观环境所提供的原始信息来决定指标权重的方法，如“聚类分析、熵值法”。使用“熵值法”来确定权重，使权重的确定更为客观科学。熵值法在社会系统应用时是指信息熵，其数学含义与物理学中的热力学熵等同，是指系统无序状态的一种度量。一般认为信息熵值与系统结构的均衡程度成正比，熵值的大小即为各指标的变异程度，因此根据熵值可以计算出各指标的权重。为了避免人为的主观影响，本文使用数据的完整样本，采用熵值法(陈明星等，2009)构建制度综合指标。
正规化处理。最终合成的指标来源于不同层次的指标体系，各个层次的具体指标值的量纲与数量级均有差异，将这些不同量纲、不同数量级的指标正规化之后，才具有横向的可比性与实用性。同时这也是构建综合指标体系必要的基础工作。
在正规化过程中，需要区分指标大小走向对整个系统的意义。当单个经济指标的值越大对制度体系发展越有利时，采用正向指标计算方法：
(2)构建制度指标体系。制度指标需要选取相关的经济指标进行综合评价。将制度指标细分为市场化程度、产业结构、开放程度、城市化水平以及受教育水平五个方面，并选取表1中所列的经济指标构建制度体系，并对各指标进行分析：
市场化程度。与其他学者的研究类似(宋德勇，1999；金玉国，2001；王文博等，2002；叶飞文，2004)，本文选择市场化程度作为制度的一个重要代理变量。由于改革开放以来，中国最为重要的制度变迁是由计划体制向市场体制的转轨，市场化程度可以很好地反映这一特征。在市场经济体制基本确立之后，制度变迁会逐渐趋于均衡，变迁速度将逐渐趋于零。本文选取私有固定资产投资比重、非国有企业产值占GDP比值、非国有单位就业人数占总就业人数比重这三个指标对市场化程度进行衡量。从1985-2011年，随着市场经济体制的逐步确立，国有企业改革进程不断推行，私有固定资产年度投资额比重逐年上升，并在2011年达到91.4%的比例；非国有企业产值占GDP比重与非国有单位就业人数占总就业人数比重也在逐年上升。在改革的市场经济体制取向逐步确定之后，更呈现出明显上升趋势，其中非国有单位就业人数随着时间推移的正向趋势更加明显。
产业结构。产业制度的变化在中国制度变迁中也是非常重要的，有些研究曾使用工业水平作为制度的代理变量(宋德勇，1999)。本文在衡量产业结构制度时，选用各产值比重、各产业就业人数比重这两个指标来进行衡量，发现在过去的20多年间，由于第一产业比重指标是逐渐下降的趋势，而第二产业的比重在过去的二十多年较为平稳，第一产业与第三产业存在此消彼长的关系，因此选用第三产业的指标作为产业制度的指标，方便制度指标体系的合理构建。具体指标为第三产业产值占GDP的比重和第三产业就业人数在总就业人口中的比重。
开放程度。开放程度的不断提高是中国制度变迁的一个重要内容。本文选取固定资产投资中外商投资额所占比重、进出口总额占GDP比重、实际利用外资总额、外汇储备、对外合作金额这五个指标对开放程度进行衡量。在该指标体系中，进出口总额占GDP比重体现了中国在世界贸易中的参与程度，这一比例随着市场经济改革的进行而逐渐增多，在2007年由于受到世界经济恶化的影响下跌，后于2009年逐渐回升；中国外汇储备总额持续上升，并在中国加入世界贸易组织后迅猛增加，于2011年达31810.21万亿美元；实际利用外商投资额在统计年份中均表现出逐年上升的趋势；固定资产投资中外商投资额所占比重在经过1995年的迅猛增加之后出现逐渐减缓的趋势。
城市化水平。城市化水平反映了一个国家城市与农村的基本结构，可以看作一个重要的制度变量。本文选取城镇人口比重与城镇固定资产投资比重这两个指标进行衡量。由于城市化水平指标的构建方法各异，也有专门的文章对城市化水平的指标进行构建，其中也有运用熵值法对城市化水平进行拟合的。因此如果直接借鉴其他城市化水平的综合指标，放入制度指标体系，并在制度指标中继续使用熵值法，会由于迭代而使信息失真，因此选用这两个比较重要的指标进行衡量。
受教育水平。由于劳动者的受教育程度会影响整个经济的发展，因而教育制度在长期中，对经济增长有着长远而深刻的影响，随着20世纪90年代末教育制度的改革，各高等院校扩招，最直接的体现就是受教育的人数有很大提高，因而选取大专以上普通高校学生和与总人口之比来衡量受教育水平，2000年以前的高等教育人口所占比重变化不大，均在0.0002以下，2000年之后高等教育人口比重逐渐上升，2011年达0.0092水平，但是总体人口高等教育普及率还不足1/100。
确立制度体系指标后，需要进行制度体系的综合评价，我们构建制度指数的基本思路是，通过熵值法替代主观的评价指标权重的办法来算出具体某年某个指标的权重，在此基础上计算出年度总得分，计算结果见表2。
(3)经济增长率。以GDP增长率(lngdp)、人均GDP增长率(lnpgdp)、第一产业增长率(lnf)、第二产业增长率(lns)以及第三产业增长率(lnt)这五个指标作为经济增长率。图1显示第二产业增长率波动最大，而第一产业增长率、第三产业增长率、人均国内生产总值增长率波动比国内生产总值增长率平缓。从时间上来看，波动在1985-1995年之间表现得更频繁。1996-2007年经济波动幅度处于平缓阶段，2008年经济危机来袭，各变量的波动性又开始显著。
2.向量自回归(VAR)实证方法准备
在进行传统回归分析的过程中，需事先确定外生变量与内生变量，而在变量之间存在相互影响的系统中，明确地区分外生变量与内生变量十分困难，识别错误会带来错误的结论。因此，在研究各因素对经济增长影响的复杂系统里，需要将这些变量放到一起，作为一个整体来预测，以得到合理的预测结果，这便是Sims(1980)提出的向量自回归模型(Vector Autoregression，记为VAR)。将经济增长率与制度水平(lni)两个因子构建为二元向量自回归系统模型，其中经济增长率分别用GDP增长率(lngdp)、人均GDP增长率(lnpgdp)、第一产业增长率(lnf)、第二产业增长率(lns)以及第三产业增长率(lnt)表示。系统的基本结构为：
注：从选取的变量看，制度水平逐年提高。在选定期内，制度水平高低表示的是一个相对水平，而不是一个绝对量。由于选取的指标都进行了正规化，因此制度水平的评分在(0，1)之间。 资料来源：熵值法计算。
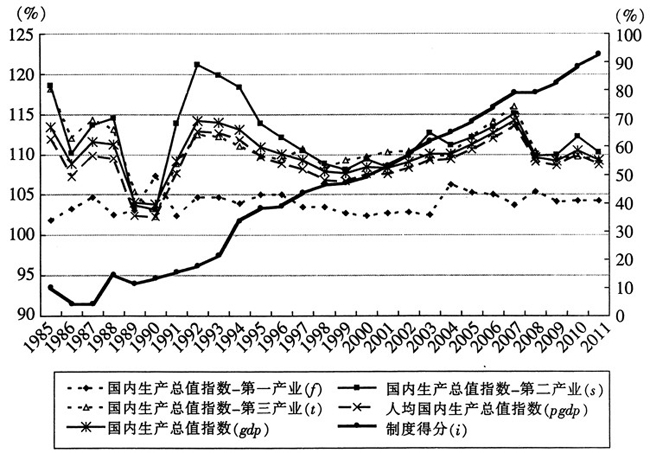
图1经济增长率变动情况(左侧纵轴)与制度水平(右侧纵轴)(%)
资料来源：国泰安数据(其中按不变价格计算，上年=100)。
其中，
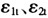为白噪声过程。此方法可根据历史数据分析经济增长率与制度之间的动态特征，除兼有时间序列及普通最小二乘方法的优点外，还可以研究在某一时刻一个变量出现随机冲击后对另一个变量的冲击效应，即脉冲响应分析。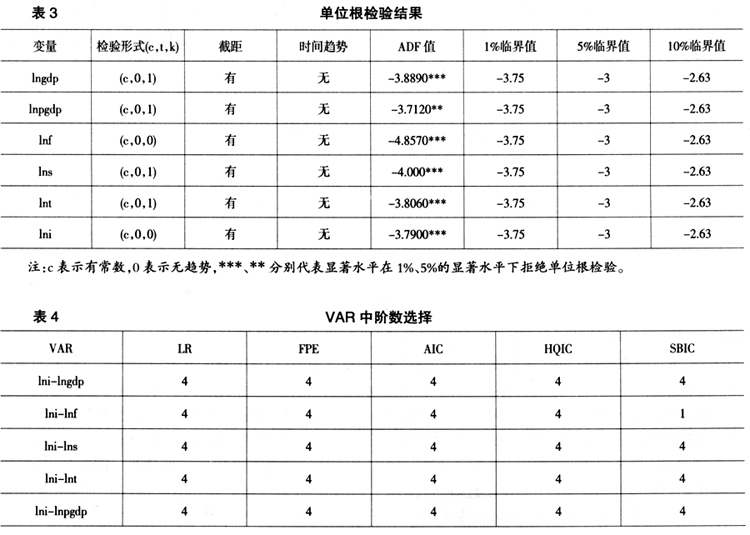
单位根检验的结果显示所有变量都是平稳的，使用Stata11将五个经济增长率指标分别与制度指标建立方程，进行VAR估计，估计结果见表4。
表4分别给出了五个方程应选择的滞后阶数，确定滞后阶数为4。进行4阶向量自回归，无论是单一的方程还是整体，其估计结果都通过了显著性检验，残差服从正态分布且不存在自相关，同时五个方程的单位根均在判别图圆内。五个方程的格兰杰非因果检验识别结果如表5所示。
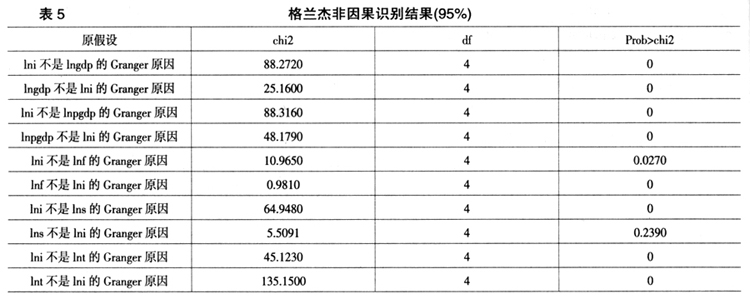
表5结果中除了“lns不是lni的granger原因”没有被拒绝之原假设外，其余原假设均被拒绝，也就是说制度是上述变量的Granger原因。
3.VAR脉冲响应
根据前文数据进行处理，得出VAR脉冲响应图(如图2所示)。
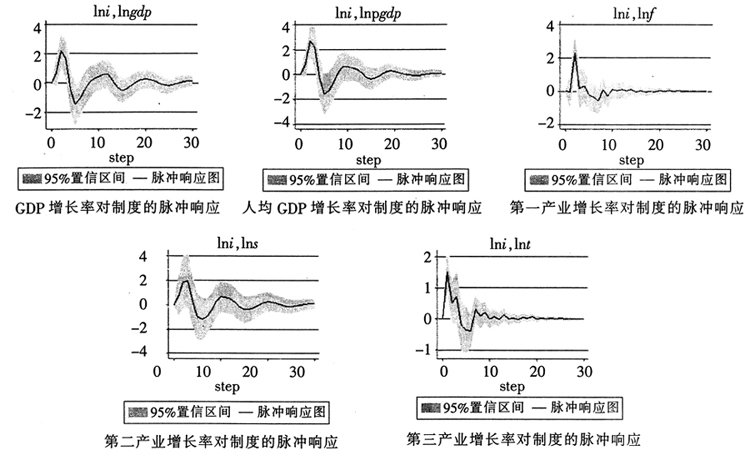
图2脉冲响应结果
根据以上研究，可以从不同视角描述制度变迁对经济增长的影响。从图2可以看出，制度变迁对经济增长在开始时有正效应的冲击，而且冲击效应相对较大，然后此效应回调，超过零边界，变成负效应，对经济增长产生阻碍，随后便微调回到了平稳的状态。
从脉冲响应结果发现，制度冲击对经济增长具有显著的振荡作用，同时不同产业之间呈现出不同的特征。由图2可知，在第一期出现了制度冲击之后，GDP增长率在前10期内波动明显，受到制度冲击的影响较显著；在10期到30期之间，GDP增长率的振荡幅度逐渐减小，制度变迁对总经济增长率的影响逐渐趋于稳定状态；在30期之后GDP增长率振荡的幅度逐渐趋于0。制度变迁对于人均GDP增长率的影响过程与此类似。制度变迁对不同产业的增长率的冲击作用则呈现出不同的特征：第一、二产业经济增长率对制度冲击的反应比第三产业更为强烈，当发生制度冲击后，第一、二产业短期内振幅比第三产业的振幅大0.5个标准差。
从制度冲击的时间效应来看，第一、三产业的增长率受到冲击影响大，时间较短，通常在10期之后，影响就趋于稳定并逐渐消失，而第二产业的增长率的波动状态类似于GDP增长率，时间周期明显长于第一和第三产业。
因此，实证检验的基本结果是，制度冲击对中国经济增长具有较长时期的效应，同时在不同产业之间呈现出不同的影响，制度冲击在第二产业中持续的作用时间比较长，波动程度相对较大；第一产业对制度冲击的敏感性较弱，持续的作用时间较短；制度冲击对第三产业经济增长率具有显著的正向作用，而这种作用在第一产业与第二产业表现不明显。
三大产业的经济增长率的波动存在不同特征的原因主要有以下几个方面：一是由于对资本的依赖性不同，第一产业和第三产业资本依赖程度较小，产业资本运营周期相对较短，因此在受到制度冲击后，可以做出快速调整，回到原有的稳定水平，而第二产业的增长率对资本的依赖程度较高，资本运营周期较长，因此波动的周期较长；二是由于政府注重程度不同，国家仍然重视工业发展，整个宏观经济水平有很大一部分是由工业构成，因此制度的变迁通常对第二产业有很大影响，其增长率波动期较长，且与GDP增长率的冲击效应相似；三是由于第三产业市场化程度相对较高，因此对制度冲击的调整更及时，波动的持续时间较短；四是第二产业增长率对制度变迁的冲击反应与GDP增长率基本吻合的这种特征，与产业内部调整具有适应性有关。
将实证检验与数理推导相结合，我们发现，制度冲击对总体经济的正向作用较强。在图2中，制度冲击发生之后经济正向波动幅度比负向的幅度要大，同时制度冲击带来的正增长效应所占的时间长于负增长效应所占的时间。制度冲击对各项经济增长率的影响都在若干时期后趋于平稳，这与前文数理部分的结论相一致，即公式(8)所显示的，在制度变迁发生若干期之后，经济增长率将会保持一个稳态值。