统计推断中若干不可检验的假定

耿直

【内容提要】

本文将讨论根据临床试验和观察性研究进行疗效评价常用的几种假定，以及在不同假定下可能出现的相互矛盾的结果。本文主要研究病因推断中处理分配机制的假定，疗效或暴露作用评价中对照个体的模型假定，不完全数据分析中缺失数据机制的假定。本文给出一些虚构的例子只是为了说明问题，并不蕴含任何医学结论。

【关 键 词】病因推断/观察性研究/不可检验的假定

        引言
        本文讨论统计模型和统计推断中的某些假定。这里的假定是指统计建模和统计推断的前提条件，在建模和推断中只认为假定都成立，并不准备论证其是否真正成立。与假设不同，在统计假设检验中，论证假设是否成立是其主要目标。尽管在一篇论文中，假定是不需要论证的，作者本来就不打算论证它，而只论证所提出的假设，但是，将该论文中所提出的方法应用于实际的时候，应用者必须确认该方法所需要的假定是否成立。如果假定不成立，那么，用该方法得到的结论也就有疑问。但是，在实际问题中，确认假定是否成立常常不是一件容易的事情，特别是有些假定在原理上是不可确认的，甚至是由经验不可证伪的。在两小儿辩日的故事中，一小儿争辩日初近而日中时远，其假定是近者大而远者小；另一小儿争辩日初远而日中时近，其假定是近者热而远者凉。孔子不能判定孰是孰非。统计学者也常常处于孔圣人的尴尬境地，尽管有一套“完整”的推理逻辑，但是，在实际应用中，很难断定谁的假定对，谁的假定不对。根据数据进行统计推断时，需要一些模型假定，其中有些假定是可以根据数据进行检验的，而另一些假定是不可根据数据检验的。比如，简单随机抽样得到的数据是否服从正态分布的假定，可以根据数据进行检验；而观察性研究中无混杂偏倚的假定，是不可根据数据检验的。
        本文将讨论实际应用中可能遇到的若干假定问题。在不同假定下中医大夫和西医大夫如同两小儿，得到完全相反的结论，而统计学者无能为力，处于尴尬的地位。
        第一节介绍处理组可交换假定和Simpson修论；第二节介绍对照组模型假定和Lord悖论，讨论对照个体模型对疗效评价的关键作用；第三节介绍逆回归问题，从不同观点出发，可能会导致不同结论；第四节讨论调查数据的缺失数据机制对统计分析结果的作用。
        表1西医大夫的论据

有效无效总和中医160 240 400西医200 200 400

        表2中医大夫的论据

 青年组 老年组总和 有效无效有效无效中医

 703090210 400西医 180 120 2080400

        一、处理组可交换假定
        一位中医和一位西医找到一位统计学者争辩他们各自的疗效好。两位大夫分别拿出了找他们看病的400位病人的临床数据。西医大夫根据表1的临床数据说：我治疗的400位病人中有200人治好了，而中医治疗的400位中只有160人治好；西医疗效显著优于中医疗效。这时，中医大夫拿出表2的数据讲：我们应该将病人分为青年组和老年组，两个组分别进行比较；青年组，中医疗效是70%，西医疗效只有60%；而且老年组，中医疗效是30%，西医疗效只有20%；不管是青年的，还是老年的，中医的疗效都比西医的疗效显著呀。似乎有道理，从表2可以看出，老年人爱看中医，青年人爱看西医；青年人恢复得快，老年人恢复得慢一些。尽管如此，这位统计学者摇了摇头，不能断定谁的医术高超。因为他知道，明天西医大夫也许会拿出表3的数据来争辩。
        表3统计学者设想西医大夫将会拿出的论据
        
        这个故事中，西医大夫的结论需要假定西医组的病人和中医组的病人是可交换的。也就是说，假若看中医的400位病人，当初不看中医而看西医的话，将得到类似于西医组病人的疗效200/400；而且当初看西医的400位病人不看西医而看中医的话，也将得到类似于中医组病人的疗效160/200。因为我们无法让时间倒退交换这两组病人，也就得不到西医组病人当初进行中医治疗的数据，所以，这个可交换假定是不可用经验数据进行统计检验的。另一方面，中医大夫的结论需要假定在青年组和老年组中中医病人和西医病人都是可交换。同样，我们也无法验证这个可交换的假定。统计学者不能判断孰是孰非。采用随机化试验可以保证处理组的可交换性。
        二、对照组模型假定
        中医大夫与西医大夫分别收集了自己治疗高血压的临床试验数据，其中记录了每位病人人组时治疗前的血压和经过一段时间治疗后的血压。中医组病人和西医组的病人的数据分别散布在如图1显示的两个椭圆内。西医大夫计算了每位病人人组时与治疗后的血压的差值，发现每个治疗组内的平均的血压下降值都是0（或者有相等的差值，比如都平均降了血压10）。椭圆以45度角直线为对称轴，反映了中医治疗和西医治疗没有差异。
         
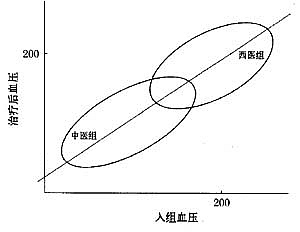
        图1Lord悖论
        为了描述中医大夫的方法，我们先描述一下回归直线的图形。图2中表示根据椭圆形的散点数据得到的回归直线，以及椭圆长轴之间的关系。回归直线比椭圆长轴的斜率平缓一些，表示预测结果向平均回归的现象。
        中医大夫采用协方差分析方法。引入一个自变量Z，令Z=0表示中医组，Z=1表示西医组。建立治疗后血压对治疗前血压和变量Z的回归模型。根据Z的系数为正、为负，或为0，来比较中医和西医的治疗效果。用协方差分析对中医组和西医组建模，将处理组用二值变量Z表示，加到回归方程中建立平行回归直线，结果如图3给出。得到处理组之间是有差异的结果，平均疗效的差异是两条直线之间的距离，也就是Z的系数值。根据所得到的两个治疗组的回归直线，可以看出在相同入组血压值的情况下，治疗后中医组将会比西医组有较低的血压。
        两位医生根据相同的数据，采用不同的方法，得到了相互矛盾的结果。哪位医生是正确的？我们应该使用血压治疗前后的差值？还是协方差分析？
        西医大夫认为：处理的结果与假若不处理的结果保持一样的话，将认为处理无效果。比如，在一个化学试验中，试剂的颜色在加入硫酸后保持不变，说明硫酸对试剂的颜色没有作用。因为不加入硫酸的话，试剂应该是不改变颜色的。隐含地假定一个病人的对照治疗的结果，在治疗后的血压将会与入组时的血压一样。也就是说，该病人经过治疗，如果没有血压变化的话，就说明他所采用的治疗与安慰剂对照相比没有效果。这个假定是不可检验的。
         
        图2椭圆形数据、椭圆长轴、回归直线
         
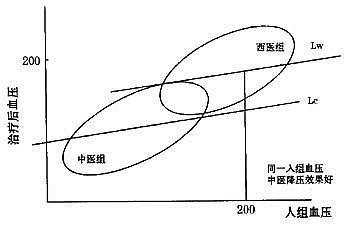
        图3平行回归模型，协方差分析
        中医大夫假定了用安慰剂作为对照的话，病人在治疗后的血压可以用他入组时的血压值进行回归预测。进一步假定了同一处理组的所有病人有相同的回归模型。即使处理无作用，处理前的血压随时间推移也不应该保持不变。处理前的血压随时间变化可能朝向平均血压回归。比如中医组的初始血压比西医组偏低，即使中医组无疗效，略高出平均血压的高血压值随时间变化应该向平均血压回归得少一些。而西医组的初始血压偏高，即使西医治疗无效果，高的血压随时间变化应该向平均血压回归得多一些。西医组保持偏高血压不变，说明西医组的降血压效果不如中医组的效果。
        两位医生针对每个个体在未治疗的状态下，其血压将会出现什么结果做了不同的假定。西医大夫假定：治疗没有效果的话，治疗的结果与假若不治疗的结果应该一样；也就是说，治疗对血压没有效果的话，每位病人入组时的血压应该多于治疗后的血压。而中医大夫假定，治疗没有效果的话，治疗的结果将会向平均回归；也就是说，即使治疗对血压没有效果的话，每位病人入组时的血压在治疗后会向平均血压回归。因为每位病人没有安慰剂处理的对照个体，不可能根据经验检验哪位医生的假定是正确的，因此，统计学者从统计分析的结果不能判断哪位医生的结论正确。
        三、逆回归问题设想中医大夫和西医大夫以不同的观点研究比较中药与西药的降血压效果。他们都想说明自己的疗效更有效。调查数据按照中医治疗组与西医治疗组，如图4中的两个椭圆所描述的那样。根据相同的调查数据，这两位医生从不同的角度同时得出了两个相反的结论。
         
        图4中医与西医的疗效比较
        中医大夫用入组血压预测治疗后血压，利用协方差分析方法建立了中医组和西医组的两条平行回归直线为L1c和L1w。由图4可以看出，他的结论是，在相同入组血压的情况下，中医组治疗后的平均血压低于西医级治疗后的平均血压；反映出中医组比西医组有更大的降血压效果。
        另一方面，西医大夫以治疗后的血压推断入组时的血压，也分别建立了中医组和西医组的两个线性回归模型为L2c和L2w。由图4可以看出，他的结论是，在治疗后有相同血压的情况下，西医组的平均入组血压高于中医组的平均入组血压；也就是说，西医组比中医组有更好的降血压效果。
        中医假定治疗前具有相同血压的病人，经两种方法治疗后，血压较低的一组具有较好的疗效。而西医假定经治疗后具有相同血压的病人，当初入组时血压较高的一组具有较好疗效。中医大夫和西医大夫从各自不同的假定得到不同的结果，单从数据的统计分析结果难判孰是孰非。
        从这个例子，我们可以看出，X与Y有两条不同的回归线，问题对回归直线的选择是敏感的；因为两个治疗组的自变量的分布存在差异导致了不同的结论。因此需要调整X的分布，将不可比的两组的自变量分布调整为同一分布后，才能进行比较。
        四、不可忽略的缺失机制
        在实际数据调查中，常常会出现缺失数据。如果数据的缺失与缺失值的大小有关，比如高工资的人不愿意告知他的收入。我们称这种引起缺失的模型为不可忽略的缺失响应机制。当数据缺失的机制不可忽略时，可能会出现不可估计的情况。设想一个随机变量有缺失的情况。例如，某疾病在若干年后会出现一种后遗症，我们通过收集病人的数据来评价该后遗症的比率。令二值变量Y:Y=0表示没有后遗症，Y=1表示有后遗症。调查中会出现某些病人不回答，或若干年后一些病人失访。所得到的不完全数据如表4所示。根据回答病人的数据估计该后遗症的比率为：
         
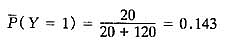
        但是，显然这个估计不能令人信服。下面我们假定不同的缺失数据机制来估计后遗症比率。
        表4后遗症调查数据

人数无后遗症(Y=0) 120有后遗症(Y=1) 20未回答，

或未调查到 60

        引入是否缺失的值是变量R，其值等于零(R=0)表示Y的值缺失，其值等于1(R=1)
         
        第三种假定也许是有后遗症的人自己会找到医院，而无后遗症的病人大部分失访。这样得到的后遗症比率比根据回答病人的数据估计的比率和随机缺失假定下的估计比率都低。
        另一种方法是，为了估计后遗症的比率，引入与结果变量Y相关的协变量X。比如治疗前疾病的严重程度，X=0表示治疗前疾病的程度不严重，X=1表示治疗前症状严重。假设治疗前症状X总是能观测到的。第四种假定是，缺失指示变量R只依赖于Y的值（即是否有后遗症），而不依赖于X的值（治疗前疾病程度）；即，假定是否告知有后遗症与是否有后遗症相关，但与治疗前疾病程度无关。这个假定用概率分布表示为，给定Y下X与R相互独立：
         
        表5X完全观测，Y有缺失的调查数据
         
        表6在第四种缺失机制假定下，采用EM算法得到的最大似然估计
         

【作者简介】耿直北京大学数学科学学院，北京100871