内容提要:条件分位数回归(conditional quantile regression,CQR)方法已成为经济学实证研究的常用方法之一。由于CQR结果的经济学阐释基于过多甚至是不必要的控制变量,这与人们所关心的问题有可能并不一致。例如,在劳动经济学对教育回报的研究中,无论个体的年龄,性别与家庭特征如何,教育程度对于个人收入的异质性影响是人们关注的重点,即人们想了解收入关于教育程度的无条件分位数估计。本文旨在介绍近年来发展起来的无条件分位数回归(unconditional quantile regression,UQR)技术并梳理相关文献。特别地,本文介绍三种重要的无条件分位数回归模型:Firpo,Fortin和Lemieux(2009)提出的再中心化影响函数(recentered influence function,RIF)回归,Frolich和Melly(2010)提出的无条件分位数处理效应模型与Powell(2010)提出的一般无条件分位数回归。另外,论文还运用一个研究居民收入分配格局变化对其医疗支出影响的实例详细说明了新方法的应用。
关键词:混合型养老金/Black-Scholes/期权定价
作者简介:朱平芳(1961-),男,浙江兰溪人,1987年毕业于上海财经大学应用统计专业,获经济学硕士学位,2005年毕业于上海社会科学院经济研究所,获经济学博士学位,现为上海社会科学院数量经济研究中心主任,研究员,博士生导师,兼任中国数量经济学会常务理事,上海市数量经济学会副理事长兼秘书长,研究方向为科技政策与科技进步;张征宇(1981-),男,浙江宁波人,2006年毕业于复旦大学数学系数学专业,获理学硕士学位,2009年毕业于上海财经大学经济学院数量经济学专业,获经济学博士学位,现为上海社会科学院数量经济研究中心副研究员,兼任上海市数量经济学会理事,研究方向为微观计量经济学。
一、引言
自从Koenker和Bassett(1978)提出分位数回归(quantile regression,QR)方法以来,其已发展成为经济学实证研究的常用方法之一。最初,QR方法仅被看作是用来替代最小二乘(OLS)估计的一种稳健(robust)估计。事实上,经济学家们在如今的实证研究,特别是基于微观数据的研究中青睐QR方法,并不在于它的稳健特性,而是可以借此方法了解解释变量对于被解释变量在扰动项的不同分位点上的异质性影响。通常,人们在评估一项经济政策对受众群体的影响时,不但希望了解政策对任一参与者的平均影响,更希望知道政策对位于特征分布不同位置(分布末端或顶端)人群的异质性作用。例如,教育对于人们收入的影响作用是劳动经济学中极具争议的问题之一。由于人的能力不可直接观测,且普遍被认为与个人的收入水平密切相关,因此,工资方程的扰动项很大意义上就是用来包含不可观测的个人能力。在这种设定下,通过分位点回归,人们可以了解对于不同能力水平的个人,可观测的个体特征如何影响他们的收入。
从以上例子不难理解,Koenker和Bassett(1978)提出的只是条件分位数回归方法。条件分位数(CQR)方法的结果实际上只告诉我们对于具有相同观测特征的个人(例如,具有某一特定年龄,家庭背景的女性),不可观测的能力差异对于收入的异质性影响。由于CQR的经济学意义阐释基于过多甚至是不必要的个体特征,其结果与政策制定者所关心的问题很有可能并不一致。例如,人们可能只想了解教育年限对于个人收入的一般边际影响,而无论个体的年龄,性别与家庭背景如何,这就是所谓收入关于教育程度的无条件分位数估计问题。解决这个问题的一个直觉想法是在计算中抛弃除了教育年限外的其他解释变量,直接用收入对教育年限进行分位数回归,但这种做法得到的无条件分位数不是一致估计。这一点类似于在最小二乘法中即使研究者只想了解某一解释变量对被解释变量的偏影响系数,遗漏剩余解释变量仍会导致所有系数估计的不一致性,除非遗失变量与所剩变量是正交的。
无条件分位数回归(unconditional quantile regression,UQR)技术正是对于CQR技术的补充和拓展,在基于微观数据的实证研究中,特别是在劳动经济学与经济政策评估中具有十分重要的意义。在这一前沿领域,国外学者的研究也只是刚刚开始,并且有关无条件分位数回归的理论与方法正在逐渐完善之中。本文旨在介绍UQR技术并梳理相关文献。特别地,我们介绍三种重要的无条件分位数回归模型:Firpo、Fortin和Lemieux(2009)的再中心化影响函数(recentered influence function,RIF)回归,Frolich和Melly(2010)的无条件分位数处理效应模型与Powell(2010)的无条件分位数回归。有关UQR与CQR的差别,本文将在第二部分“无条件分位数回归的最新进展”中详细说明。
另外,本文试图用一个研究居民收入分配格局变化对其医疗支出影响的实例说明新方法的应用。该实例将说明居民总体收入分配格局的变化如何影响其医疗支出的分布,而已有基于条件分位数回归技术的文献无法对这一问题做出全面的回答。运用新方法的实证结果表明:在控制了疾病严重程度与城乡差异等因素后,由收入引起的居民医疗消费不平等显著存在;居民收入的按量(by amount)增长无法改善这种不平等,而收入的按比例(by proportion)增长对医疗高消费人群的拉动作用远大于对低消费人群的作用,因而进一步加剧了这种不平等性。
二、无条件分位数回归的最新进展
(一)RIF回归
假设已经获得了被解释变量Y以及可能影响Y的k维解释变量X的观测值。我们关心的是X的变动对Y的影响。例如研究者时常关心以下条件分位数偏效应(conditional quantile partial effects,CQPE)的估计值:

问题1:仅当收入发生微小改变时,引起所有具备特征X=x的个体组成群体的Y分布τ-条件分位数的变化量①。
CQPE尽管可以帮助我们回答问题1,但是却无法回答下面虽与问题1密切相关,但有明显区别的另一问题:
问题2:当整个人群的收入分布发生微小变化时,他们的Y分布的τ-分位数将产生何种变化?
问题2与问题1的相似之处在于两者都是关心X的边际变动对Y分布的影响;两者的显著不同是:问题1只是针对整个人群中的某一(具有特征X=x)子人群而言,而问题2是针对整个人群整体而言。
一般地,我们需要了解X分布的微小变化对于被解释变量Y无条件分布τ-分位数的影响。这等价于计算以下无条件分位数偏效应(unconditional quantile partial effects,UQPE):

来获得UQPE的估计。为应对这一难题,Firpo,Fortin和Lemieux(FFL,2009)借用稳健估计(robust estimation)中影响函数(influence function)的基本概念,建立了估计UQPE的一般步骤。该方法的基本思想如下:利用统计学中稳健估计的若干知识,可得以下恒等式:


将式(6)与式(5)右边相减,除以增量Δx并令Δx趋向于零,可以得到X的单位平移变换对Y的τ-无条件分位数的边际影响,即无条件分位数偏效应:
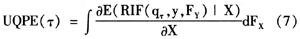
最后,FFL建议从式(7)出发,通过以下三步获得UQPE的一致估计:

来获得UQPE(τ)的一致估计。
(二)无条件分位数处理效应
处理效应模型和普通的回归框架探究变量之间的相关关系不同,它研究的是变量之间的因果关系,允许研究者在十分弱的假定下获得变量之间因果关系的准确估计,因而在微观经济政策评估中占据十分重要的地位。假设D是一个0-1处理变量。D=1表示个体接受了某种政策,D=0表示未接受这种政策。用
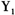 与
与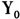 分别表示个体在D=1或D=0状态下的结果。平均处理效应(average treatment effect)E(
分别表示个体在D=1或D=0状态下的结果。平均处理效应(average treatment effect)E(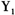 -
-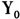 )表示的是该政策对潜在受众对象的平均作用大小。但是,政策的平均影响并不是政策制定者关心的全部内容,通常他们还关心政策对于群体在整个分布不同分位点上的异质性影响,这等价于需要估计如下的分位点处理效应(quantile treatment effect,QTE):
)表示的是该政策对潜在受众对象的平均作用大小。但是,政策的平均影响并不是政策制定者关心的全部内容,通常他们还关心政策对于群体在整个分布不同分位点上的异质性影响,这等价于需要估计如下的分位点处理效应(quantile treatment effect,QTE):
FM首先注意到并非所有个体的QTE都可以被识别出来,而只有那些可以通过变动工具Z来改变他们处理状态D的遵从者(complier)的QTE才能被识别出来。其中,遵从者当D=1时的分布函数
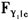 满足
满足
可以看出的是,要通过式(10)和式(11)的逆函数来求解式(12)其实十分困难。为克服这一难题使得UQTE便于计算,FM采用了再赋权(reweighting)分位点回归的算法,其主要思路如下。定义权重函数
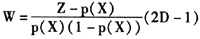
其中p(X)=E(D=1|X)。在以上权重下,可以证明式(10)和式(11)具有等价表示
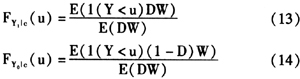
为计算在特定τ处的UQTE,令式(13)和式(14)的等号的左边都等于数值τ,即得

其中
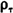 (u)=u(τ-1(u<0))。基于以上思路,实际计算可分为三步,首先获得得分倾向p(X)的非参数估计p(·),随后代入W的表达式获得W的一致估计
(u)=u(τ-1(u<0))。基于以上思路,实际计算可分为三步,首先获得得分倾向p(X)的非参数估计p(·),随后代入W的表达式获得W的一致估计
(三)无条件分位数回归
回顾以上两类对UQR的研究,Powell(2010)认为,FFL的RIF回归虽然具备无条件分位数回归的思想,但是它将所有解释变量都等同于控制变量,即RIF回归无法同时基于一些变量的条件分位数回归时计算另一些变量的无条件分位数回归。另一方面,FM的无条件分位数处理效应无法推广到处理变量取值为连续的一般情形。Powell(2010)考虑以下回归方程
Y=g(D,X,ε)(17)
其中Y是被解释变量,D是政策变量,X是反映个体特征的一组控制变量,ε是不可观察的扰动项。这里区分政策变量与控制变量的目的主要是为了计算Y关于D是有条件的分位数回归,同时关于X的部分分量是无条件分位数回归。这种部分无条件分位数回归在实际应用中具有极大的灵活性,因为,人们可以根据研究目的自由地选择自己想要了解哪些解释变量对于被解释变量的异质性作用。例如,当人们想要了解教育对于工资的分位数影响时,可以令D只包含教育变量,而将其他有关个人性别、年龄、家庭背景等因素全部放入控制变量X中。此时部分无条件分位数回归结果回答的问题将完全不同于FFL的RIF回归结果回答的问题,当然也不同于一般条件分位数回归结果回答的问题。
为简单起见且能够说明部分无条件分位数回归的基本想法,Powell只考虑当Y关于D的无条件分位函数是线性的情形。在这种情况下,式(17)可以进一步写成
Y=αD+U(X,ε)
其中
E(P(U(X,ε)≤0|D,X)|D)=τ(18)
比较式(18)与CQR框架下对应的条件可以帮助我们理解UQR与CQR的重要区别。在CQR中,我们有
P(ε≤0|D,X)=τ(19)
将式(19)与式(18)对比,可以发现UQR实际上计算的是D对被解释变量Y在由控制变量X与真正的误差项ε一起组成的扰动项分布不同分位点上的异质性作用。
需要指出的是,为了计算Y有条件的关于D同时无条件的关于X的分位数回归,直接用Y对D进行条件分位数回归的做法是有问题的。首先,一般来说X与D是相关的。即使D和X各自与ε独立,也会因为X与D的相关导致D与复合扰动项U(X,ε)是相关的。换句话说,即使方程本身不具有内生性问题,也会因为无条件分位数回归的定义导致计算时出现内生性问题。第二,即使X与D不相关,直接用Y对D进行条件分位数回归会导致X中包含的信息未加充分利用而使得估计量是无效的。为了克服这些问题,Powell(2010)将UQR框架的基本假设用以下两个矩条件进行了概括:
P(Y-αD≤0|D,X)=
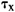
(20)
与
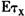 =τ(21)
=τ(21)其中矩条件式(20)实际上只是一个排除性约束。因为一般来说,式(20)的右边应该同时是X与D的函数。在线性假设正确的前提下,如果αD是Y有条件的关于D同时无条件的关于X的分位函数,那么Y的τ分位数中不能由αD解释的部分,只可能是X的函数,而不会再与D相关。矩条件(21)是矩条件(20)的一个附带约束,它说明剩余部分虽然可能随X变动,但是均值为τ,这说明当前估计的是τ分位点上的无条件分位函数。容易说明式(20)和式(21)是CQR的一个自然推广。与UQR相比,可以认为CQR中所有的解释变量都在D中,因此X就不再存在。于是式(20)的右边就变成常数τ,这正是CQR对应的矩条件。结合式(20)与式(21),以及它们与CQR的联系,可以得到估计参数α的一般方法,即
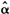 (τ)可以通过最小化以下目标函数得到
(τ)可以通过最小化以下目标函数得到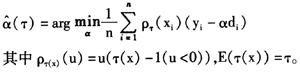
三、实证例子
(一)研究背景
中国经济三十多年的高速增长见证了人民生活水平的日益提高与健康状况的极大改善。我国居民出生时的预期寿命已由1980年的67岁延长到2004年的71岁,超过世界平均水平4年;婴儿死亡率则由1980年的49‰下降到2004年的26‰。与此同时,国内居民的收入差距也在迅速扩大。据国家统计局的数据显示,自2000年开始,我国基尼系数已越过0.4的警戒线,并逐年上升。世界银行估算,2009年中国的基尼系数已攀升至0.47,国内居民收入最高与最低各10%家庭之间的收入差距,已从21倍扩大到55倍。不断扩大的收入差距已成为我国经济发展中的一个突出问题,对社会与人民生活的各方面都产生了重要影响。面对同时出现的收入差距扩大与居民健康医疗需求的增长,正确理解收入与健康之间的内在联系,特别是如今收入不均现状下居民医疗卫生需求行为的基本特征正成为公共卫生政策制定者与经济学家关心的问题。早期Grossman(1972)等人的人力资本模型表明,收入提高有助于改善人们的健康状况。此后国外大量基于微观数据的经验证据显示,健康不仅与收入的绝对水平正相关,也与收入的分布特征,即收入不平等的程度有关。Kennedy等人(1998)、LeClere等人(2000)的研究表明:美国,人们的收入差距和健康水平之间有很强的负相关性。关于收入不平等影响健康的机制,Wilkinson(1996,2004)认为,收入差距通过增加低收入人群的挫败感以及压力,使其染上吸烟、酗酒、吸毒等不良的行为习惯或焦虑、抑郁等心理疾病,从而恶化其健康水平。在这一方面,国内学者也做了大量的实证研究。Li&Zhu(2006)使用中国的微观调查数据研究发现,社区的收入不平等程度会显著影响居民自我报告的健康状况,并且这种影响呈现倒U型;同时收入不平等也对居民的健康行为(如吸烟、喝酒)有影响。封进等人(2007)使用同样的数据,得到了类似的结论。
收入不平等影响健康的另一可能途径是收入差距导致的医疗卫生服务利用的不平等性。医疗卫生体系中的平等是指这样一种状态:同等需要应得到同等保健(equal need ought to be treated equally),即医疗需求不与个体的收入、地域、种族有关而只与其年龄、自身健康状况等变量相关。当医疗服务利用受到了收入等非必需类变量的影响,即认为医疗服务不平等是存在的。张晓波(2003)使用不同来源的数据考察了中国的医疗系统中存在的各种不平等现象,并对不平等的成因进行了分析。魏众等人(2005)考察了家庭收入和家庭医疗支出的经验联系。文章从城乡医疗资源配置的合理性质疑我国医疗卫生体制的公平性,并建议国家应该采取措施引导医疗补贴流向农村地区,特别是西部地区。齐良书(2006)强调了收入分布不均等性以及居民社会经济地位特征的差异对于其健康与医疗支出水平的重要影响;最近,解垩(2009)利用中国家庭健康营养调查CHNS数据计算了收入因素对健康不平等、医疗服务利用不平等的贡献,指出我国存在亲富人,亲高收入人群的健康不平等与医疗服务利用不平等。同样基于CHNS数据,林相森等人(2009)通过估计Tobit模型,得到了类似的经验证据。
以上文献在不同程度上丰富了有关健康公平的研究,在讨论时均强调收入不平等对健康与医疗服务利用不平等的贡献作用。另一方面,随着整体收入差距的不断上升,中国的收入分配格局实际上处于一个不断变化的过程中。从制定政策的角度,我们更关心这样的问题:居民总体收入分配格局的改变将对目前医疗服务利用平等性的变化趋势产生何种影响?由于医疗费用直接度量了医疗资源的利用,因此,本文将直接研究居民总体收入分配格局的变化对其医疗支出分布的影响。从计量分析的角度来讲,这是一个研究解释变量分布的变化对于被解释变量分布边际影响的问题。可以说明的是,常见的均值回归或CQR技术,均无法对这一问题作出完整的回答。为此,本文借助于近来发展起来的UQR技术,基于中国家庭健康营养调查CHNS2006数据,重点考察了居民整体收入分布的两种边际变动,即按量变动,对应于收入分布的平移变换(location shift)与按比例变动,对应于收入分布的尺度变换(scale shift),对于人群医疗消费分布的影响。
(二)数据
本文使用的数据来自“中国健康和营养调查”(CHNS)数据集。该调查始于1989年,覆盖了国内9个省(辽宁、黑龙江、山东、江苏、河南、湖北、湖南、广西、贵州)的城镇和农村。相比于其他年份的数据,2006年的调查问卷调整了与医疗支出相关的部分问题,从而使得调查数据的质量有很大提高。因此,本文将采用2006年数据进行研究。我们选取2006年调查中的患病成年人作为研究样本,他们在调查之前的4周内均出现过不同程度的疾病症状。这样的样本包括2015个成年人,占所有9788个成年人中的20.6%。考虑到收入这一变量在本文研究中的重要地位,我们注意到这2015个成年人中有相当一部分,特别是农村老年人的收入记录大多为零。尽管这些年老体弱者的收入十分微薄甚至为零,但他们医疗需求却是极其强烈的。此时,无论是将这些人的收入变量不加处理直接作为零放入模型进行估计或简单地将他们从样本中删除都是不恰当的。一个合适的做法是:考虑到低收入老年人的医疗支出通常是由家庭中有经济能力的其他成员,例如子女承担,因此本文用家庭人均收入代替个人的收入。同时CHNS数据内容的确包含个人从属家庭编号的信息,因此这种做法在技术上也是可行的(同时对CHNS数据采用这种做法的文献有解垩(2009))。本文把各个家庭成员的工资、奖金、补贴以及农业收入按家庭求和,再除以家庭人口得出人均收入。在这些处理之后,仍然有一些个人的家庭人均收入结果为零③。随后我们又把这些家庭人均收入为零的个体从样本中剔除,最后的样本包含1365个成年人,年龄分布在21岁至80岁之间。
(三)计量方法
在运用UQR方法分析收入分布变动对居民医疗需求分布的影响时,我们发现实际研究过程出现的几个问题需要我们对已有的理论方法进行一定的拓展。需要指出的是,以下拓展不但适用于本文研究的问题,对其他应用该方法的实证研究也同样适用。


可以得到分量
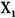 的单位尺度变换对Y的τ-无条件分位数的边际影响,即仅第1个分量尺度变换下的无条件分位数偏效应计算公式:
的单位尺度变换对Y的τ-无条件分位数的边际影响,即仅第1个分量尺度变换下的无条件分位数偏效应计算公式:

(四)变量定义
本文采用个人医疗支出(hcexp)作为被解释变量,把各个家庭成员的工资、奖金、补贴以及农业收入按家庭求和,再除以家庭人口得出人均收入作为个人收入(inc),其他的控制变量还有:(1)疾病严重程度(分为1-3等,数字越大疾病严重程度越高);(2)户籍(城镇户口用1表示,农村户口用0表示);(3)性别(男性用1表示,女性用0表示);(4)是否参加了医疗保险(参加了用1表示,没有参加用0表示);(5)年龄(21岁至80岁);(6)教育程度(分为1-5等,数字从小到大分别表示:小学或其以下学历,初中或其以下学历,高中、职校或其以下学历,大学本科或其以下学历,研究生或其以下学历)。以上各变量的描述性统计量见表1。除此以外,为了对本文主要关心的医疗支出与收入变量的分布特征有一个粗略地了解,我们还可以用核密度估计的方法绘制它们的密度函数图(图略)。
(五)实证结果
为了与下面的无条件分位数回归结果作对比,我们首先用条件分位点回归方法估计如下的Tobit模型:

算法估计模型(25)中的系数。在实际计算中,我们采用R软件中的quantreg程序包对模型进行估计,并将其他系数的分位点估值及其t统计量总结在表2(见下页)。

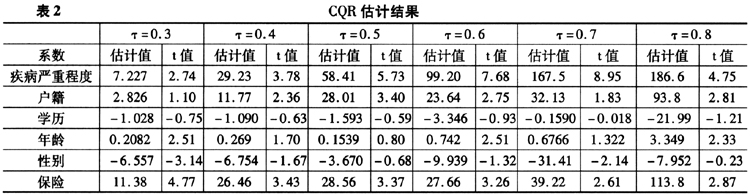
从表2可以看出除收入以外的其他因素对个人医疗支出的影响。例如,疾病严重程度对医疗支出的贡献随分位点的上升而不断提高,这表明严重的疾病是引发医疗消费高的重要原因之一,超常的巨额医疗支出更有可能是因为疾病严重程度本身而导致的。同样,户籍属性对个人医疗支出的差异性也有显著贡献;医疗支出水平越高,城镇户口相对于农村户口在获得医疗服务方面的优势越突出。但是,并非所有的因素对医疗支出的影响都呈现这种单向的走势:性别对个人医疗支出的贡献尽管存在,但是随分位点的变化波动不太剧烈,显得比较平稳。
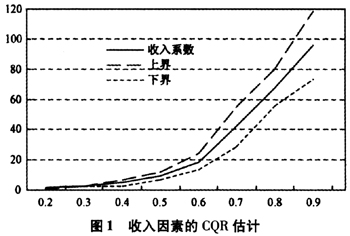
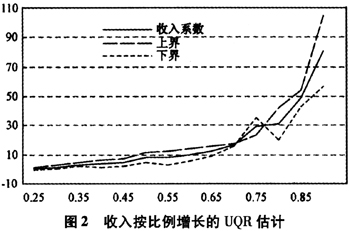
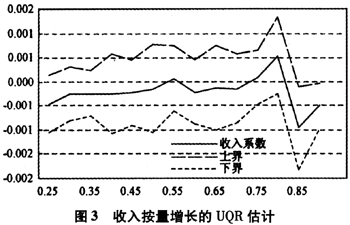
总的来说,收入对于医疗支出的影响仍然呈现单调上升的变化趋势:医疗支出的水平越高,收入对医疗支出差异的贡献也越大。这表明收入差距导致的医疗服务利用不平等显著存在。这也是众多检验医疗服务平等性文献所得到的共识。根据前述关于CQR与UQR方法在经济学问题阐释方面的区别,以上结果无法告诉我们当整个人群的特征分布,例如收入分布产生变化时,对医疗支出分布的边际影响。这使得我们转向对应的UQR估计。我们采用第二部分2.1中所叙述的步骤(i)-(iii)来估计收入分布的变动对于医疗支出分布的边际贡献。我们考虑两种不同类型的收入分布的边际变动:平移变换与尺度变换,分别对应每个人的收入增加1元时与每个人的收入增加1%时对总体支出分布各分位点的影响。从图2和图3可以看出,收入分布的两种不同变动对于整个人群医疗支出分布的影响特征是完全不同的:具体来说,在其他因素不变的情形下,假如每个人的收入都在其原来的基础上增加1%,那么医疗支出原本在中低水平的人的支出金额将有小幅的提高,但是高医疗支出的人群将显著提高他们的医疗支出。这意味着收入的按比例增长对医疗高消费人群的拉动作用将远大于低消费人群的拉动作用。收入按比例增长将进一步加剧医疗服务利用的不平等性。另一方面,在其他因素不变的情形下,如果每个人的收入在其原来基础上增加1个单位,那么这种变动对医疗支出的分布影响比较微弱,大部分时候都是不显著的。
四、总结
尽管条件分位数回归有助于研究者了解各解释变量X对于被解释变量Y在扰动项的不同分位点上的异质性边际影响,然而,在实际问题的研究中,人们时常面临以下两难选择。一方面,他们集中关心的只是X中极少数变量对于Y的影响。另一方面,为了确保参数的识别与一致估计,他们又不得不在模型中包含X的其他变量。近年来发展起来的无条件分位数回归较好地解决了这一问题。无条件回归技术允许人们在保证模型准确识别与参数一致估计的前提下了解解释变量对于被解释变量无条件分位数的边际影响。本文在讨论条件分位数回归与无条件分位数回归概念区别的基础上,重点介绍了三种重要的无条件分位数模型架构。除了单纯的理论介绍之外,我们还用一个研究居民收入分配格局变化对其医疗支出影响的实例详细说明了新方法的应用。通过这一实例,读者可以清晰看出两种方法在解释经济学问题上的联系与差异。
注释:
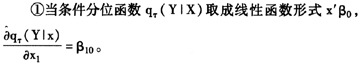
②与此不同的是,条件均值的期望等于无条件均值,这被称为条件期望的迭代法则。
③导致这一结果的原因除了被调查者本身隐瞒了其收入的情况,还有因为家庭中有经济收入的个人在调查当日因各种原因未能参与到调查活动中来。
参考文献:
[1]胡琳琳.我国与收入相关的健康不平等实证研究[J].卫生经济研究,2005(12).
[2]解垩.与收入相关的健康及医疗服务利用不平等研究[J].经济研究,2009(2).
[3]刘宝、胡善联.收入相关健康不平等实证研究[J].卫生经济研究,2002(1).
[4]林相森、舒元.我国居民医疗支出影响因素的实证分析[J].南方经济,2007(6).
[5]赵忠、侯振刚.我国城镇居民的健康需求与Grossman模型[J].经济研究,2005(10).
[6]Abadie, A., Angrist, J. and Imbens, G. Instrumental variables estimation of the effect of subsidized training on the quantiles of trainee earnings[J]. Econometrica, 2002(70): 91-111.
[7]Blundell, R. and Powell, J. L. Endogeneity in nonparametric and semi-parametric regression models[J]. Advances in Economics and Econometrics: Theory and Applications, 2003.
[8]Firpo, S., Fortin, N. M. and Lemieus, T. Unconditional quantile regressions[J]. Econometrica, 2007(77): 953-973.
[9]Frolich, M. and Melly, B. Unconditional quantile treatment effects under endogeneity. working paper, 2008.
[10]Horowitz, J. L. and Lee, S. Nonparametric instrumental variable estimation of a quantile regression[J]. Econometrica, 2007(75): 1191-1208.
[11]Imbens, G. W. and Newey, W. K. Identification and estimation of triangular simultaneous equations models without additivity[J]. Econometrica, 2009(77): 1481-1512.
[12]Koenker, R. and Bassett, G. Regression quantiles[J]. Econometrica, 1978(46): 33-50.
[13]Kress, R. Linear Integral Equations[M]. Second Ed. New York: Springer. 1999.
[14]Newey, W. K., and Powell, J. L. Instrumental variable estimation of nonparametric models[J]. Econometrica, 2003(71): 1565-1578.
[15]Powell, D. Unconditional quantile regression for exogenous or endogenous treatment variables. Working Paper, 2010.
