会员登录
会员注册内容提要：将面板数据模型和多水平模型结合起来，提出了多水平面板数据模型。通过分析该模型的方差协方差结构，采用迭代广义最小二乘法和限制迭代广义最小二乘法，导出模型的参数估计，并通过模拟数据进行了比较分析。结果认为：与多水平模型和面板数据模型相比，该模型能更好地拟合具有层次结构的面板数据。
关键词：多水平模型/面板数据模型迭代广义最小二乘法限制迭代广义最小二乘法多水平面板数据模型
作者简介：王尚坤，女，重庆巫山人，经济学硕士，四川理工学院理学院讲师，研究方向：统计理论及方法（四川自贡643000）；石磊，男，云南大理人，云南财经大学统计与数学学院教授，研究方向：应用统计（云南昆明650221）。
一、引言
由于我们所处的社会具有分级结构，因而很多社会经济研究都涉及嵌套或分层数据。传统的线性模型的基本假设是线性、正态、方差齐性及其独立性，而方差齐性和独立性的假设在具有嵌套或分层结构的样本中往往是不成立的。对这些分层数据的分析，传统的最小二乘（OLS）估计方法已经不再适合，由此发展了多水平模型[1]15-159[2]28-168。多水平模型（Multilevel Models）又称为分层线性模型（HLM，Hierarchical Linear Modeling），它是20世纪80年代由英美教育统计学家提出的，是专门针对具有嵌套或层次结构数据发展起来的一种新的统计模型。例如，当数据处于两个层次时，先以第一层的变量建立线性回归模型，然后分别以该线性回归模型的系数作为第二层解释变量的线性函数，建立第二层的线性回归模型，通过这样建立模型，就可以同时处理不同层次、跨层次变量之间的关系，还能将不同层次间的误差项考虑进来，进而估计出各个层次上的差异性。
事实上，面板数据也可以看成是具有层级结构的分层数据[3-4]。近几十年，绝大多数研究者对面板数据的分析多采用面板数据计量模型，较少考虑面板数据的分层结构。面板数据模型中的变截距面板数据模型、变系数面板数据模型与多水平模型有很多相近的地方[5]141-175。张旭、石磊对两水平模型与静态面板数据模型进行了对比分析，指出了两者间的区别与联系，以此将多水平模型与面板数据模型结合起来，但没有对该模型的估计理论及相关问题进行深入研究[6]。基于此，笔者将同时考虑面板数据的层次效应和时间的随机效应，分析多水平面板数据模型的方差协方差结构，导出模型参数的估计方法，并通过模拟数据对模型进行验证分析。
二、多水平面板数据模型
多水平面板数据模型是将多水平模型和面板数据模型结合起来，同时考虑数据的层次效应和时间的随机效应。由于面板数据是对同一样本多次重复观测得到的数据，重复观测嵌套于个体对象中，因而将重复观测作为第一水平，个体作为第二水平，同时在第一水平还引入时间随机效应。下面详细介绍两水平面板数据模型。
（一）两水平面板数据模型的一般形式
在成熟的多水平模型和面板数据模型的理论基础上，两水平面板数据模型的一般形式如下
水平1模型可表述为：
水平2模型可表述为：
将（2）（3）代入式（1），得到组合模型为：
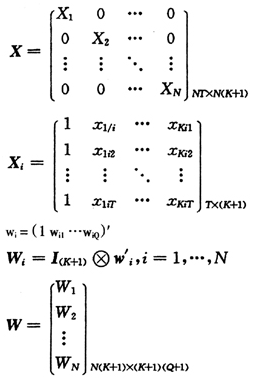
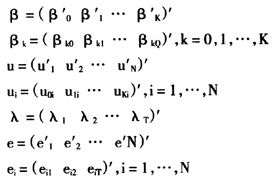
传统的两水平模型不考虑时间效应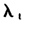
，而面板数据模型一般不考虑回归系数的随机性和层次效应，因此模型（1）是两水平模型和面板数据模型的有机结合。
（二）两水平面板数据模型的假设条件
根据多水平模型和面板数据模型理论，对模型（1）（2）（3）可作如下假设：
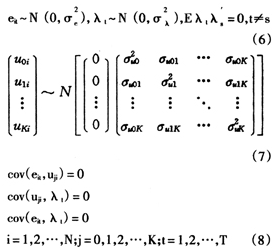
（三）两水平面板数据模型的方差结构
模型（5）包含两部分，一部分是固定效应XWβ，另一部分是随机效应部分。随机效应部分用ε表示如下：
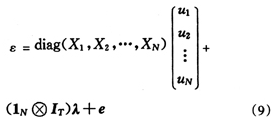
由前面的假设条件（6）（7）（8），可以得到模型的协方差结构：
（四）两水平面板数据模型的参数估计
根据多水平模型理论及其估计方法，可以采用迭代广义最小二乘估计（IGLS）和限制迭代广义最小二乘估计（RIGLS）对模型（4）（5）进行参数估计[7]。
IGLS和RIGLS都是从普通最小二乘（OLS）开始估计固定回归系数，计算出OLS残差及其方差协方差矩阵V，然后以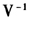
为权重的广义最小二乘法（GLS）来估计模型随机参数的方差协方差矩阵。这些估计出来的方差协方差矩阵又被用来作为新的GLS的权重，重新估计固定回归系数，又计算出新的GLS的残差及其方差协方差矩阵。这两部分的计算交替进行，直到估计过程收敛。
1.迭代广义最小二乘估计（IGLS）
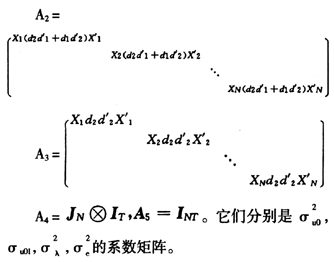
若θ已知，则固定效应参数β的最佳线性无偏估计就是广义最小二乘估计：
当给定β和θ一个初始值，IGLS估计就开始在式（13）与（15）之间进行迭代计算，直到迭代收敛，就可以估计出固定效应参数β和随机效应参数θ的值，β和θ的协方差分别为：
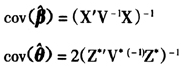
2.限制迭代广义最小二乘估计（RIGLS）
IGLS对参数θ的估计是一个有偏估计，当θ给定时：
由于笔者提出的多水平面板数据模型的方差结构更复杂，不能采用现有的多水平统计软件进行参数估计，故本文编写了Matlab程序对模型的参数进行估计。
三、模拟分析
为了验证上述估计方法对于多水平面板数据模型是否可行，首先，对于模型（1）～（3）中水平1只有一个解释性变量，水平2不含解释性变量的模型，模拟数据进行验证。模型结构如下：
水平1模型可表述为：
针对模型（19），假定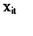
是从标准正态分布中随机选取的数据，并且根据模型假设条件（6）（7）（8），取参数
的一组真实值。根据这组真实值，模拟1 000次200个个体在10个时间点的观测值，得到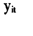
和
组成的面板数据，将该数据应用到模型（19）中，并分别采用IGLS和RIGLS对模拟数据进行参数估计。
由于每次参数估计结果与真实值之间都有一定的偏差，将1 000次估计结果作进一步的处理。首先，对各参数的1 000次估计结果进行平均，用来说明参数估计值与真实值之间的平均偏差程度；其次，用1 000次样本参数估计的标准差的平均值表示结果的波动程度；最后，考察在0.05的显著性水平下，各参数在1 000次估计结果中显著次数的比率，可以用来说明参数估计结果的可信度，用显著率表示。将参数估计分析结果显示在表1（见下页）中。
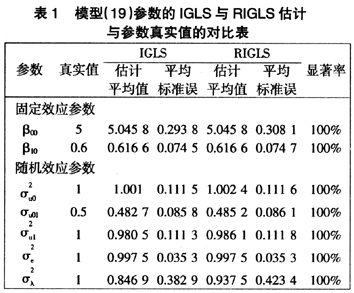
从表1知，参数的估计结果都显著，这说明参数的估计结果是可信的。
首先，从参数估计结果的平均值来看，参数估计结果的平均值与真实值之间都相当接近，这说明参数估计结果与真实值之间的偏差程度很小；参数估计结果的平均标准误都比较小，说明参数估计值的波动程度较弱。IGLS和RIGLS对参数的估计结果差别不明显，但是RIGLS的无偏性更好，因此这两种参数估计方法都可以运用到该模型中，并且都可以得到比较好的估计结果。
其次，对于模型（1）～（3）中水平1只有一个解释性变量，水平2也含一个解释性变量的模型，模拟数据进行验证。模型结构如下：
水平1模型可表述为：
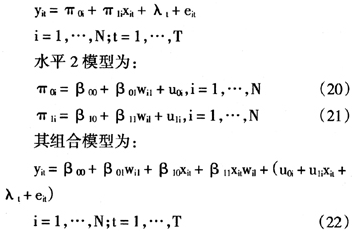
对于模型（22），假定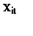
与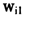
都是从标准正态分布中随机选取的数据，并且根据模型假设条件（6）（7）（8），取参数
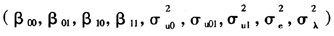的一组真实值。根据这组真实值，模拟1 000次200个个体在10个时间点的观测值，得到
，
组成的面板数据，将该数据应用到模型（22）中，并分别采用IGLS和RIGLS对模拟数据进行参数估计，将1 000次估计结果按照前面的分析方法进行分析，分析结果显示在表2中。
从表2可以看出，在显著性水平为0.05的情况下，参数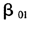
与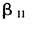
的估计值90%都显著，其他参数的估计结果全都是显著的。在IGLS和RIGLS两种估计方法下，各参数的估计平均值与真实值之间的偏差都很小，平均标准误也说明了在估计过程中的波动程度不大。
最后，按照前面模拟数据进行参数估计的方法，将两水平面板数据模型与两水平模型、二维随机误差分解模型进行比较分析。当模型（16）中不含时间随机效应时，其组合模型（19）变为：
从表3可以看出，两模型中的参数估计结果在0.05的显著性水平下都显著。从两模型的参数估计结果的平均值与真实值的对比可以看出，两模型中的参数估计值与真实值的偏差都很小。由于两水平模型没有考虑时间效应的影响，因而参数估计结果中，时间随机误差的影响效应被当成了模型的设定误差考虑，参数
的估计结果大于真实值。这说明两水平面板数据模型能够详细地解释模型中方差变异的来源。
从模拟数据估计的过程中还发现，虽然模型（19）与模型（23）的估计结果中固定效应参数的估计值相当接近，随机效应参数
的估计值也相差不大，但是每次估计结果中，模型（19）的似然比检验统计量-2LL的值都要小于模型（23）的似然比检验统计量-2LL的值。本文随机选取一次估计结果中的-2LL值，显示在表4中。
从表4知，模型（23）与模型（19）的-2LL的差分别为203.8，215.4，与自由度为1的
分布的临界值（置信水平设为0.05，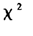
（1，0.95）=3.84）相比都是显著的。由于似然比检验统计量可以用来衡量拟合模型的优劣，-2LL的值越小，表示模型拟合得越好，并且统计量还达到了显著水平。因此，模型（19）比模型（23）能更好地拟合数据，这说明用真实模型（19）能得到更好的拟合效果。
对于模型（16）～（19），若没有考虑到数据的层次效应，则模型就是典型的二维随机误差分解模型[9]34-56，可将模型表示为：
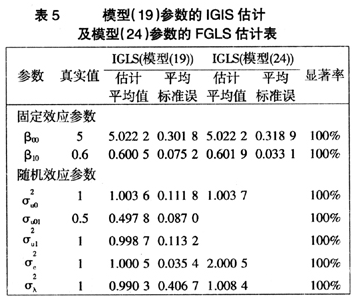
从表5中可以看出，两种不同的模型中，固定效应参数的估计结果与参数真实值之间相差都很小，参数估计结果的波动幅度也不大，但是对于不同模型，其解释变量解释的结局测量变异有很大的不同。两水平面板数据模型的结局测量值受到不同层次效应、时间效应及其模型随机误差效应的影响。而面板数据模型的结局测量值受到个体随机效应、时间随机效应和模型随机误差效应的影响，它没有考虑数据的层次结构，造成参数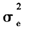
的估计值大于其真实值。并且在模拟数据估计的过程中，模型（24）中AIC的值都要大于模型（19）中AIC的值。本文分别随机选取一次估计结果中的AIC的值，显示在表6（见下页）中。
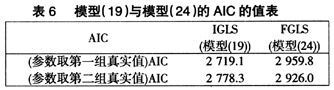
从表6知，模型（24）中AIC的值都要大于模型（19）中AIC的值。从模型的拟合优度来看，AIC的值越小，说明模型拟合数据更好。因而，真实模型（19）比模型（24）对数据的拟合程度更好。
四、结论
对于实际问题中需要研究的面板数据，应该根据研究的不同目的、不同内容，从多方面加以分析，找到适合的模型对数据进行建模。多水平模型和面板数据模型都可以分析面板数据。多水平模型可以分析不同层次的数据，通过建立不同层次的模型，解释组群效应和个体间的差异，但不能体现随机时间效应的影响。面板数据模型则可以很好地刻画个体异质性，在模型中可以引入个体和时间随机因素，但是它不能分析数据的层次效应。
多数面板数据都是通过随机选取N个个体在T个时间点的观测值，相对于总体来说，个体和时间都存在随机因素，在分析实际问题时，不应该忽略这些随机效应的影响。本文提出的多水平面板数据模型是一个新型的模型，它结合了面板数据模型和多水平模型的优点，能够分析具有层级结构的数据，同时还能在模型中引入时间随机因素，充分考虑个体、组群的差异性，更详细地解释模型中方差变异的来源。
模拟估计的结果显示，多水平面板数据模型比多水平模型和二维误差分解模型能更好地拟合具有层次效应的面板数据。同时，多水平模型的建模思想、估计方法同样适合于多水平面板数据模型。同时，IGLS和RIGLS两种估计方法能够很好地估计多水平面板数据模型的参数。
参考文献：
[1]Raudenbush S W, Bryk A S.分层线性模型：应用与数据分析方法[M].郭志刚，等，译.北京：社会科学文献出版社，2007.
[2]Goldstein H. Multilevel Statistical Model[M].2nd ed New York: Halsted Press, 1995.
[3]Shi L, Chen G. Case Deletion Diagnostics in Multilevel Modds[J]. Journal of Multivariate Analysis, 2008, 99(9).
[4]Shi L. Ojeda M M. Local Influence in Multilevel Regression for Growth Curves[J].Journal of Multivariate Analysis, 2004,91(3).
[5]Cheng Hsiao. Analysis of Panel Data[M].北京：北京大学出版社，2005.
[6]张旭，石磊.多水平模型及静态面板数据模型的比较研究[J].统计与信息论坛，2010(3).
[7]Goldstein H. Multilevel Mixed Linear Model Analysis Using Iterative Generalized Least Squares[J].Biometrika, 1986, 73(1).
[8]石磊.多水平模型及其统计诊断[M].北京：科学出版社，2008.
[9]白仲林.面板数据的计量经济分析[M].天津：南开大学出版社，2008.