后金融危机的货币供给过剩及其效应

内容提要：本文针对我国货币政策的操作特征，使用阈值协整方法扩展现有的货币需求模型，度量后金融危机时期的货币供给过剩及其对通胀与经济增长的非线性调节效应，并进而设定广义脉冲响应函数揭示货币供给过剩对通胀与经济增长的冲击效应。主要结论为：2009年第三季度以后，我国货币供给过剩且过剩幅度快速增加，其中名义M1过剩12.56%，名义M2过剩11.31%。2009Q3—2010Q3我国处于货币供给过剩机制下，在该机制下，央行谨慎地实施从紧货币政策，从紧货币政策对通胀和经济增长的调节效应相对较强。货币供给过剩对通胀和经济增长的冲击在前2年为正值，在随后近3年为负值。这说明我国现阶段适度宽松货币政策的退出必须谨慎，退出速度不宜过快。

关键词：货币供给，金融危机，非线性调节，冲击效应

作者简介：欧阳志刚、史焕平，华东交通大学经济管理学院，邮政编码：330013，电子信箱：oyzg2001@sina.com，emshp@tom.com。本研究得到国家自科基金项目（70971040，71040004）、国家社科基金重点项目（10AZD014）、教育部人文社会科学项目（09YJC790085）、教育部全国优秀博士论文基金的资助。作者感谢匿名审稿人对本文提出的宝贵修改意见，但文责自负。

一、引言

为应对全球金融危机的冲击，我国政府果断地实施了宽松货币政策，并取得预期效果。随着全球金融危机冲击的弱化和逐步消退，我国经济实现复苏，并在2010年出现经济过热的迹象。适度宽松货币政策是否应该退出？央行对此举棋不定。出现这种局面的主要原因在于，央行难以相对准确地度量现阶段货币供给过剩的程度，特别是难以相对准确地判断货币供给过剩对通胀与经济增长影响的幅度和持续的时间。在这种情况下，如果盲目地收紧货币政策，则可能失去金融危机后来之不易的复苏成果。因此，如何准确度量后金融危机时期货币供给过剩的程度？怎样刻画货币供给过剩对通胀与经济增长的调节效应？如何揭示货币供给过剩对通胀与经济增长的冲击方向和持续时间？准确回答这些问题对于现阶段适度宽松货币政策的退出，对于宏观经济的稳定运行具有重要的现实意义。本文将基于我国货币政策的操作背景，改进现有货币需求函数的估计和检验方法，并针对后金融危机的货币供给过剩状况，设定广义脉冲响应函数系统以回答上述问题。

近期对货币供给过剩和货币供给不足的度量多数是建立在货币数量方程的基础上，其中主要有价格缺口法、真实货币缺口法、名义货币缺口法和货币过剩法（Polleit and Gerdesmeie，2005）等。使用价格缺口法、真实货币缺口法、名义货币缺口法度量货币供给过剩必须首先计算产出、货币供给、价格等变量的潜在值，而现阶段国内外对经济变量潜在值的测度仍存在较大分歧，并且不同方法所得到的潜在值可能差异很大。使用货币过剩法度量货币供给过剩，需要计算均衡货币供给量，而均衡货币供给量是基于货币需求函数得到，因此，实证分析中是否适合使用货币过剩法取决于货币需求函数的长期稳定性。根据王少平、李子奈（2004）、伍戈（2009）等的研究，我国存在长期稳定的货币需求函数。因此，相对于其它方法，基于货币需求函数的货币过剩法可能更适合度量我国后金融危机的货币供给过剩。

从货币需求函数文献可以看出，自Engle & Grangle（1987）和Johansen（1995）提出线性协整的概念后，现有文献多数是基于线性协整方法研究货币需求的长期稳定性及其短期调节，如Juselius（1996）、Beyer（1998）等。从模型设定看，现有文献的货币需求模型一般遵循了基本的货币需求理论，即名义货币需求的主要影响因素包含名义收入、价格水平及持有货币的成本和收益等，写成公式即为：

Md/p=f(Y/p，z） （1）

其中，Md和Y分别表示名义货币需求和名义收入，p表示价格水平，z表示其它影响货币需求的变量。出于不同的研究目的和不同的实际经济背景，实证研究对z中变量的选择不尽相同。Banerjee et al.（1993）的解释变量包括收入、利率和通胀率，他们使用英国的数据研究发现，货币需求、收入、利率和通胀之间存在协整关系。Ball（2001）在解释变量中引入收入和利率，对美国战后数据研究表明，美国的货币需求函数长期稳定，其中收入弹性约为0.5，利率半弹性约为-0.05。王少平、李子奈（2004）的解释变量包括收入和利率，基于线性协整框架研究了我国货币需求函数的长期稳定性和短期因果关系，发现我国货币政策效应主要体现在促进经济增长。叶光等（2007）的协整分析发现，真实货币余额、总产出、通货膨胀率和利率之间存在两个长期均衡关系，货币政策在促进经济增长和控制通货膨胀两个方面都发挥了重要作用。伍戈（2009）的解释变量中包含物价、产出、利率、汇率以及股票价格，研究结果表明，只要适当考虑资产替代并利用科学的计量方法，依然可以得到稳定的广义货币需求函数。

上述文献所考察的货币供给向长期均衡的动态调节和货币供给的短期调节对产出与通胀的效应都是线性的。也就是说，无论货币供给是过剩还是不足，或者货币供给偏离均衡的程度有多大，货币供给向长期均衡的回复速度和调节效应都是相同（线性）的。早在上世纪，国外学者就发现货币供给向均衡的短期动态调节以及货币政策的调节效果具有非线性。例如，Muscatelli & Spinelli（1996）、Wolters et al.（1998）的研究表明，经济衰退时期比经济上升时期的货币供给更具有易变性，从而使得不同经济状态下货币供给向长期均衡的动态调节特征不一致，导致货币供给的短期动态调节不是线性的，而是非线性（非对称）的。类似地，Calza ＆ Zaghini（2006）认为在不同经济状态下，代理人向均衡调整其投资组合的成本不一致，从而导致货币供给向均衡的短期调节具有非线性。除了货币供给自身调节的非线性外，一些学者（Nobay ＆ Peel，2003）还发现央行货币政策偏好是非对称的。也就是说，中央银行面对相同程度，但不同方向的产出偏离，会实施不同程度的货币政策操作，以此来应对经济过热和偏冷，同样地，央行在面对通货膨胀和通货紧缩时亦会采用不同的货币政策措施。央行货币政策的这种非对称操作也会导致货币供给短期动态调节的非线性。此外，在货币政策短期操作效果方面，近期文献也发现其有显著的非线性。Laurence ＆ Mankiw（1994）的研究表明，货币政策在经济衰退阶段对宏观经济效果要比在扩张阶段的效果更强。Weise（1999）发现，正向和负向的货币供给冲击对通胀与产出的效应具有非对称性，当初始经济增长率较低时，货币供给冲击对产出的效应较强而对通胀的效应较弱。Karamé ＆ Olmedo（2002）对美国的研究发现，紧缩性货币供给冲击对通胀与产出具有非对称效应。

显然，使用线性VECM无法准确刻画现实经济中的货币供给向长期均衡的动态调节的非线性。基于此，计量经济学家在线性VECM模型中引入非线性函数，以此刻画货币政策短期动态调节及其调节效应的非线性特征。从现有文献看，VECM模型中的非线性函数形式主要是TR（threshold regressive）或STR（smooth TR）形式。使用TR刻画的货币供给向均衡的非线性回复及其非线性调节效应是在几个机制间跳跃变化，因而其非线性特征是离散的而非连续，使用STR模型刻画的货币供给向均衡的回复及其调节效应是在不同机制之间平滑转换，因而其非线性特征是连续的。因此，在刻画货币供给的短期动态及其调节效应的非线性方面，STR模型更有吸引力（Chen and Wu，2005）。基于此，现有许多文献在VECM引入STR模型（简称STVECM）研究不同国家或地区的货币需求函数。例如，Sarno（1999）使用STVECM的研究表明，英国和意大利的货币需求函数具有显著的非线性调节特征。Wolters et al.（1998）、Lütkepohl et al.（1999）使用STVECM研究了德国货币需求函数中误差校正模型的非线性。Teräsvirta & Eliasson（2001）在误差校正模型中引入STR非线性形式，研究了英国的广义货币需求函数。Chen & wu（2005）的研究表明，在考虑交易成本的情形下，线性VECM不适合研究货币需求函数，对于美国和英国的数据而言，指数平滑转移函数更适合描述货币需求函数中VECM的非线性。Haug & Tam（2007）分别针对美国的M0、M1、M2，使用STVECM模型发现其货币需求函数中短期调节的非线性特征。从现有的文献对STVECM模型的估计与检验方法看，它们都是在估计STVECM前假定协整向量已知。这种假定在研究一价定律这类实际问题时可能是现实的，但在货币需求函数的研究中假定协整向量已知则不现实，且过于苛刻。Hansen & Seo（2002）正是针对现有STVECM模型估计方法的上述不足，将协整向量由已知扩展为未知。因此，尽管Hansen & Seo（2002）使用两机制TR模型刻画VECM中的非线性，但从方法论和实际应用的角度看，Hansen ＆ Seo（2002）的方法相对更好。基于此，本文使用Hansen ＆ Seo（2002）的方法研究我国的货币需求函数。

除了上述TR和STR模型外，还有一些文献使用其它非线性函数描述VECM的非线性：Calza ＆ Zaghini（2006）认为货币供给的非线性短期动态调节效应随着某个不可观察的机制转移变量的变化而在不同机制间转换，因此他们使用马尔科夫机制转移模型扩展了线性VECM。他们发现欧洲的M1的短期调节效应具有非线性。Muscatelli ＆ Spinelli（1996）使用误差校正项的立方型函数扩展了线性VECM，发现意大利的货币需求函数具有显著的非线性。Ericsson et al.（1998）、Escribano（2004）同样使用立方型的非线性VECM模型，分别研究了英国不同时期的货币需求函数，发现非线性VECM更适合描述货币供给的短期动态调节并得到了更高的拟合优度。①

二、货币需求阈值协整模型的设定及估计

（一）货币需求阈值协整模型的设定

由于我国不同时期货币政策的基本目标是保持物价水平基本稳定并兼顾经济增长，并且利率调节已成为我国不同时期的货币政策的主要操作手段，因此，我国货币政策的研究中应包含总产出、通货膨胀以及利率等变量；另一方面，基于McCallum ＆ Goodfriend（1988）的理论推导，收入、通胀和利率是影响货币需求的主要因素。基于此，本文的货币需求模型设定为：

lnmt=β0+β1lnyt+β2lnrt+β3lnpt+εt （2）

其中m=M/p，y=Y/p。如果模型（2）中的变量为I（1）过程，且误差εt～I（0），则模型（2）为协整模型，它反映货币需求函数的长期均衡关系。在货币市场均衡的假定下，由模型（2）中长期均衡关系所估计的lnmt即为均衡的货币需求量，与相等的货币供给即为我国均衡的货币供给，因此，模型（2）估计的误差εt则为真实的货币供给与均衡的货币供给之差。根据货币过剩法，真实的货币供给与均衡的货币供给之差即为货币供给过剩（或不足）的度量，因此，误差εt＞0对应货币供给过剩，表明货币政策偏松；εt＜0对应货币供给不足，表明货币政策偏紧。

进一步，针对我国货币供给向长期均衡的调节速度和调节效应的非线性特征，本文参照Hansen and Seo（2002），设定阈值协整误差校正模型（TVECM）②：

这里，协整向量β=（β0，β1，β2，β3），协整误差εt-1（β）为误差校正项也是阈值变量，γ为阈值参数，1（.）为指标函数。显然，模型（3）所刻画的货币供给向均衡的调节过程及其调节效应依赖于阈值变量εt-1（β）与阈值参数γ的相对大小，由此称为非线性调节。进一步，bi、ci（i=1，2，3）为误差调节系数，它们分别反映在不同机制下模型（2）中各变量长期稳定（协整）关系对货币供给、产出和通胀率的短期变化所产生的非线性调节效应。若b1、c1为负，表明长期稳定对货币供给的短期变化具有抑制作用，从计量的角度看，b1、c1为负也印证了模型（2）的协整关系。进一步，若协整误差εt-1≤γ，TVECM服从低机制，调节效应由At=（b1，b2，b3）所刻画；若εt-1＞γ，TVECM服从高机制，调节效应由A2=（c1，c2，c3）所刻画。特别是，若γ=0，则表明调节效应依赖于货币供给相对于货币需求的过剩或不足而发生机制转换。进一步，若A1和A2在统计上具有显著的差异，表明货币供给向长期均衡调节，以及货币供给对通胀、经济增长（产出）的调节效应具有显著的非线性，这是模型（3）的核心。

（二）货币需求阈值协整估计方法

本文使用Hansen & Seo（2002）的方法对模型（2），（3）进行估计与检验，具体步骤如下：

1.首先使用Johnsen（1995）协整方法估计模型（2），获得协整向量，协整残差以及协整向量的标准差。然后将协整残差按升序排列得到，将的第22—42个元素做为阈值参数γ的格子区间[γl，γu]。将协整向量的置信区间作为β的格子搜索区间[βl，βu]。

2.对格子区间中的每一组值，分别计算。

3.在ut独立同分布的假定下，最小化的（β，γ）就是待估计的。

（三）货币需求阈值协整的检验方法

Hansen & Seo（2002）使用SupLM统计量检验阈值协整，其原假设为H0：B1=B2（调节效应为线性），备择假设H1：B1≠B2（调节效应具有非线性）。③进一步，为表述方便，令X1（β，γ）和X2（β，γ）分别表示Xt-1（β，γ）D1t和Xt-1（β，γ）D2t的列堆栈矩阵（把列作为行堆起来），ξ1（β，γ）和ξ2（β，γ）分别表示的列堆栈矩阵。其中，是在原假

这里，υec表示矩阵向量化算子，线性协整向量的估计量作为β。

三、估计与检验结果

（一）变量及数据说明

本文的样本期间为1995年第1季度至2010年第3季度，货币供给分别选择为M1和M2。由于目前我国存款利率没有市场化，而同业拆借利率是我国市场化程度最高的利率之一，能够较真实体现资金价格，为此本文选择商业银行7天同业拆借利率（r）的季度平均值度量持有货币的机会成本。p为季度消费者物价指数（1994年=100），Y以季度名义GDP表示。M1、M2和Y都用物价指数换算成实际数据m1、m2和y，并且m1、m2，p和y都用X11方法褪去季节趋势。1995年的同业拆借利率数据来自谢平、罗雄（2002），其余数据来自中国人民银行网站和中经网数据库。

（二）变量的单位根检验

本文首先检验变量数据是否由单位根过程生成，然后使用上述阈值协整方法对模型（2）、（3）进行估计与检验。使用ADF方法对模型（2）中变量的平稳性检验，结果见表1。

由表1可知，所有变量均为I（1），因此，本文的数据生成过程吻合阈值协整模型的要求。

表1 数据的单位根检验

变量	检验形式(C，T，K)	ADF	结论
lnm1	(C，T，1)	-2.32(0.42)	I(1)
Δlnm1	(C，0，0)	-6.49(0.00)	I(0)
lnm1	(C，T，1)	-2.42(0.37)	I(1)
Δlnm2	(C，0，0)	-5.14(0.00)	I(0)
lnr	(C，0，0)	-1.47(0.54)	I(1)
Δlnr	(0，0，2)	-5.86(0.00)	I(0)
lny	(C，T，4)	-0.79(0.96)	I(1)
Δlny	(C，0，0)	-3.49(0.11)	I(0)
lnp	(C，T，2)	-1.95(0.62)	I(1)
Δlnp	(C，0，2)	-3.24(0.02)	I(0)

注：（C，T，K）分别表示ADF检验方程中包括常数项、时间趋势项和滞后阶数，括号内是对应统计检验的双尾概率。

（三）货币需求的阈值协整检验

基于前述的阈值协整检验与估计方法对模型（2）、（3）进行估计与检验。为说明方便，本文先报告阈值协整检验结果，然后报告阈值协整的估计结果。

SupLMm1、SupLMm2分别表示用m1、m2作为货币供给计算的阈值协整检验统计量，计算结果见表2。由于SupLM统计量收敛于复杂的随机泛函，因此，为此本文借助Hansen & Seo（2002）提出的固定回归元的bootstrap仿真试验以实现小样本下对SupLM统计量的显著性检验。仿真实验得到的5%显著性水平的SupLM临界值一同列入表2。

表2 阈值协整统计检验结果

统计量	估计值	5%临界值	结论
SupLMm1	69.3	52.6	拒绝原假设
SupLMm2	64.5	53.1	拒绝原假设

表2表明，本文的SupLMm1、SupLMm2统计值分别为69.3、64.5，分别大于该统计量的右尾临界值52.6、53.1，可以在5%的显著性水平上拒绝原假设。这一结果证实在货币供给相对过剩和不足的不同状态下，货币供给量的变化对宏观经济的调节效应具有显著的差异，即货币政策对宏观经济的调节具有非线性效应。

（四）货币需求协整方程的估计结果及分析

使用上述方法估计得到的货币需求协整方程如下：④

由阈值协整检验和估计结果表明，本文考察的各变量之间存在长期均衡的协整关系，因此，我国存在长期稳定的货币需求函数。从表3的估计结果看，我国货币供给对GDP的弹性为正，对利率和通胀的弹性为负，与理论预期相符。⑤这一结果说明，央行能够根据我国经济发展变化，对货币供给量中介目标进行主动调节，有助于货币政策目标的实现。

表3 货币需求函数的估计结果

	截距	lny	lnp	lnr	R2
lnm1	0.99(1.15)	1.20(20.78)	-0.15(-8.23)	-0.25(-1.04)	0.994
lnm2	2.52(3.36)	1.29(29.45)	-0.49(-2.57)	-0.12(-7.70)	0.996

进一步，货币需求协整模型（2）估计的残差е即为实际货币供给与货币需求（均衡货币供给）之差，若e＞0，货币供给过剩，表明货币政策偏松；若e＜0，货币供给不足，表明货币政策偏紧。不同时期货币政策的松、紧状态的估计结果见图1。

从图1看出，使用M1和M2所度量的样本期货币供给过剩与不足的结果基本一致。1997年前货币供给相对不足，主要原因是央行为抑制经济过热和通胀过高而紧缩银根导致的。1997年短暂的货币供给过剩则是源于1996年货币供给增长速度（如M1增速为18.9%）的快速反弹带来的累积效应。1999年后的货币供给不足是由于亚洲金融危机冲击导致的银行“惜贷”，企业“惜投”，使得货币供给增长速度大幅度下滑而形成的，其中2000年M2增长率仅为12.3%，创同期历史最低值。为应对亚洲金融危机，央行从1998年起开始实施“稳健”的货币政策，连续两次大幅度地下调存款准备金率（下调7%）。但从操作效果看，虽然1999年M1和M2的货币供给不足有一定程度改善，但随后又很快转入货币供给相对不足，由此表明这一时期的“稳健”货币政策操作力度过小，导致了较长时间的低增长、通货紧缩的不利局面。

图1 估计的残差em1和em2

从2009Q3开始，货币供给过剩开始出现，且过剩的幅度迅速增加，其中2010Q3的实际lnm1过剩0.127，实际lnm2过剩0.121。将这一数据换算成名义值，2010Q3M1过剩12.56%，M2过剩11.31%，亦即2010Q3名义M1超发了27508.9亿，名义M2超发了75587.95亿（经季节调整后）。从图1还可直观看出，2010Q3的过剩幅度大于以往。可以预期，随着美国宽松货币政策的实施，如果我国继续执行适度宽松的货币政策，未来一段时期内，我国货币供给过剩的局面将继续持续，且程度还可能增加。

（五）TVECM模型的调节参数估计结果及含义

协整方程揭示了均衡的货币供给量，TVECM模型中调节参数的估计结果则刻画了货币供给向长期均衡调节的非线性特征以及不同机制下货币供给对经济增长和通胀的非线性调节效应。TVECM估计结果见表4。

表4 调节参数的估计结果

注：括号内为t-统计值。为节省篇幅，本文只报告了模型（3）调节系数的估计结果。

阈值参数的估计结果为0.009、0.006，接近0，因此，货币政策对通胀与经济增长的调节效应在lnm1、lnm2相对需求过剩0.009、0.006的位置发生机制转换。进一步，0.006对应货币供给不足，对应货币供给过剩，由此意味着货币供给向长期均衡调节以及货币供给对通胀、增长的调节效应随着货币供给过多与不足的转换而有非线性。

调节参数的估计结果为负，这从理论上进一步印证了货币需求的长期稳定性。该结果表明，伴随着我国经济发展所形成的货币供给、总产出、同业拆借利率和通胀的长期稳定关系，对货币供给的短期变化产生抑制效应，一旦短期货币供给偏离长期均衡，货币供给向长期均衡靠拢。进一步，表4结果表明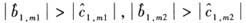，这一结果印证了前述阈值协整的检验结论，它所揭示的经济含义是：当货币供给不足时，货币供给增加的速度较快；当货币供给过剩时，货币供给降低的速度相对较慢，这也表明央行对紧缩性货币政策的实施较为谨慎。上述结论与我国的货币政策实施基本一致。例如，2008年下半年货币供给不足（见图1），央行较快提高货币供给增长速度，仅12月份的M1增长速度就比上月快2.3个百分点。2007年货币供给过剩，央行虽实施了紧缩性货币政策，但力度较小，货币供给增长率没有显著下降，其中2007M1同比增长21%，增速比上年还高3.5个百分点。特别地，后金融危机时期我国货币供给过剩，适度宽松的货币政策应逐步退出，但央行却在退出适度宽松货币政策问题上左右摇摆。上述估计结果正好刻画了央行货币政策操作的这种特征。

调节参数反映不同机制中，货币供给对实际经济增长的调节效应；的结果则反映不同机制中货币供给对通胀的调节效应。具体来看，在货币供给不足机制中，的估计结果为正意味着央行扩大货币供给增速对实际经济增长和通货膨胀具有刺激效应，但这几个调节系数的估计结果相对较小，且统计不显著，说明在货币供给不足时期，货币政策效果相对较弱。这一结果同时也意味着在亚洲金融危机时期货币供给不足，央行增加货币供给的政策有助于抑制通货紧缩和刺激经济增长，但实际上1999—2001年我国M1和M2的平均增长率较低。货币政策操作力度相对较弱给经济复苏带来不利影响，在一定程度上导致了亚洲金融危机时期较长时间的低增长、通缩局面。在全球金融危机时期，央行不仅较大幅度降低利率，同时也以较大幅度提高货币供给增长率，从而使得我国率先走出金融危机低谷。由此说明，相对亚洲金融危机时期，全球金融危机时期货币政策的操作更适宜、有效。另一方面，的估计结果为正表明货币供给过剩时，央行为达到长期均衡而降低货币供给增长速度，此时的货币政策会降低经济增长速度和抑制物价上涨。例如，在2004年的货币供给过剩时期，央行降低货币供给增长率的紧缩性货币政策能够降低短期的经济增长速度和抑制通货膨胀，从而起到抑制经济增长过热和物价上涨过快的作用。2009Q3以后，我国处于货币供给过剩机制中，连续增加的货币供给过剩程度推动了我国经济增长和通货膨胀，且这种调节作用相对货币供给不足机制中的调节作用较大。这一结果同时也说明，适度宽松货币政策的退出对于抑制当前持续走高的通胀率将起到显著调节作用，但同时也将抑制经济增长。因此，为保增长、防通胀，适度宽松货币政策退出的同时应继续实施积极的财政政策。

综上，本文设定的货币需求阈值协整模型的估计结果基本准确地度量了后金融危机时期货币供给的过剩程度，揭示了我国货币供给过剩对通胀与经济增长的调节效应。由此引出本文需要进一步讨论的问题：后金融危机时期货币供给的过剩对通胀与经济增长形成何种冲击，持续时间有多长？

四、货币供给过剩对通胀与经济增长的冲击

（一）估计方法

上述分析表明，应对全球金融危机的宽松货币政策的实施对于我国宏观经济的复苏起到显著的推动作用，但伴随而来的是2009Q3以后较大幅度的货币供给过剩，以及我国经济增长速度和通胀率的持续走高。因此，准确认识现阶段货币供给过剩对未来一定时期通货膨胀与经济增长的冲击方向和持续性，对于提高现阶段货币政策的针对性、灵活性、有效性，显然具有重要意义。广义脉冲响应函数正是适用于这一类问题的研究方法。前述检验结果表明变量xt=（lnmt，lnyt，lnrt，1npt）′存在协整关系，且各分量都是I（1）过程。因此，Δxt为平稳过程。Johansen（1995）证明了，存在协整关系的xt经差分后（Δxt）可表述为向量自回归（VAR）模型：

其中，Φi为4×4系数矩阵。由于协整系统xt各变量都是取自然对数形式，因此Δxt表示协整系统中各变量的增长率。进一步，平稳变量的向量自回归模型可等价表述为无限阶移动平均过程，因此，模型（6）等价表述为模型（7）：

这里，Ai为4×4系数矩阵，可由公式Ai=Φ1Ai-1+Φ2Ai-2+…+ΦkAi-k计算得到，且当i＜0时Ai=0，A0为4×4单位矩阵。为描述随机扰动对VAR系统的冲击效应，Koop et al.（1996）的广义脉冲响应函数为：

其中，Ωt-1为t期以前的历史信息，ut=（u1t，u2t，u3t，u4t）′为VAR系统中各变量在t期遭遇的随机冲击强度。由Pesaran ＆ Shin（1998），Δx对t期冲击ut的响应值为GIΔx（n，u，Ωt-1）=Anu。但这种计算方法是假定随机冲击不相关，而在实际经济中，随机冲击u各分量之间可能存在相关性。正是由于u各分量之间存在相关性，使得我们不能直接基于ut计算广义脉冲响应值。Sim（1980）使用Cholesk方法对u进行正交分解，即有RR′=Σ。这里R为4×4下三角矩阵。这样正交变换后的（7）式可写为：

根据Pesaran & Shin（1998）的推导，模型（7）中第j（=1，2，3，4）个方程的随机扰动ujt在t期的冲击，正交变换后经过n期对Δxt+n的效应为：

这里，是第j个元素为1，其余元素为0的4×1列向量。根据（10）式即可计算货币供给过剩对通胀与经济增长的冲击幅度和持续性。从上述计算方法的介绍也容易看出，广义脉冲响应函数是由本文模型（2）导出，从而体现本文计量方法的一致性。

（二）货币供给过剩对通胀和经济增长的冲击效应

我们首先估计了模型（6），根据最小AIC准则，Δlnm1、Δlnm2对应的最优滞后期k=6，由此得到回归系数矩阵和残差ut的估计结果。由于本文目的是研究危机后货币供给冲击对通胀和增长的动态效应，因此图2中报告了模型（6）中第一个方程估计的残差（um1，um2），即货币供给冲击。

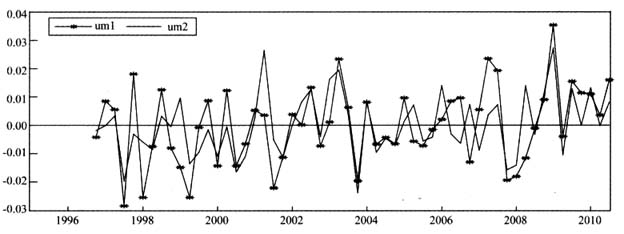
图2 不同时期货币供给冲击

连续的正向货币供给冲击可能导致随后的货币供给过剩，而连续的负向货币供给冲击则可能导致随后的货币供给不足。图2的结果不仅吻合了我国的实际经济运行和货币政策操作的背景，也与图1中的估计结果基本一致。1998—2000年，我国连续遭遇负向的货币供给冲击，由此导致1999—2001年的货币供给不足；2002—2003年我国遭遇连续正向的货币供给冲击形成了2004年的货币供给过剩。特别地，2007Q4—2008Q3我国连续遭遇负向货币供给冲击，以及2009Q1出现较大幅度正向货币供给冲击，较准确地刻画了全球金融危机时期我国的货币政策状况。图1显示2009Q3开始我国连续出现货币供给过剩，图2表明2009Q3后我国仍然连续出现正向货币供给冲击，其中2009Q3—2010Q3的M1和M2冲击强度为：，。这一结果不仅印证了前述基于货币需求协整方程所估计的货币供给过剩结果，而且说明，2010Q3后，我国还可能在一定时期内存在货币供给过剩。

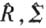为计算后金融危机货币供给过剩对通胀与经济增长的冲击效应，我们根据估计的计算模型（7）中的系数矩阵Ai，对估计的残差进行Cholesk正交分解，由此得到。基于上述结果，我们首先选择并计算近期我国货币供给过剩的典型时期，货币供给冲击对通胀与经济增长的冲击效应，以此作为参考对照。2003年是我国较典型的货币供给过剩时期（见图1、图2），且2003年是我国从亚洲金融危机的萧条中走向复苏的时期，因此，基于2003年历史数据的分析结果对现阶段货币政策的操作具有较重要的指导意义。为简便，以货币供给M1为例，设定货币供给冲击初始期t为2003Q1—2003Q3，根据图2的估计结果，设定2003Q1—2003Q3的冲击强度为=（0.0013，0.0233，0.0063）′。货币供给冲击对通胀率的效应（mp2003）和经济增长率的效应（mg2003）分别见图3。

图3 通胀率和经济增长率对2003年货币供给过剩的广义脉冲响应

从图3容易看出，mg2003在最初6个季度为正，在第7季度至第13季度为负，随后逐步衰减并在零线上下波动；mp2003在最初2个季度为负，然后转为正值并持续至第7季度，随后下降为负值，并在约5年后衰减为零。上述结果表明，2003年的货币供给过剩冲击对经济增长率的正向影响持续6个季度，对通胀率的正向影响持续至第7季度，随后的冲击影响都转为负。从受上述冲击影响的实际经济运行来看，2004年我国的经济增长率和通胀率都保持较高水平，其中经济增长率为10.1%，通胀率3.9%。从2005Q2开始，我国通胀率开始下滑，但经济增长率仍保持高增长。通胀率下滑一方面是由于2003年货币供给过剩的冲击效应开始转为负，另一方面，央行在2004年调高了法定存款准备金率，降低了货币供给增长率，导致货币供给转向不足（见图1、图2），两方面冲击效应的叠加形成了2005年通胀率的下降。2005年我国经济增长率没有下降，是因为技术进步等有效供给能力改善的强有力推动，从而弥补了货币供给冲击对经济增长率的负向效应。2003—2005年货币政策的操作以及这一时期经济增长率和通胀率的运行模式，特别是技术进步对经济增长的正向推动作用，为2010年后适度宽松货币政策的逐步退出提供了经验借鉴。

上述典型历史时期数据的分析表明，由本文广义脉冲响应函数估计结果所揭示的货币供给过剩对通胀与经济增长的冲击效应，基本准确地刻画了我国相应时期经济增长与通胀的实际运行，由此意味着，本文的模型应能较准确估计2009Q3以后货币供给过剩对通胀与经济增长的冲击效应。为此，本文设定货币供给冲击初始期t为2009Q3—2010Q3，根据图2的估计结果，分别设定M1的冲击强度为=（0.015，0.011，0.011，0.004，0.016）′，M2的冲击强度为=（0.013，0.001，0.013，0.0001，0.008）′，对应的通胀率和经济增长率的响应分别见图4和图5。

图4 通胀率和经济增长率对M1的冲击响应

图5 通胀率和经济增长率对M2的冲击响应

这里，m1p和m1g表示通胀率和经济增长率对M1冲击的响应，m2p和m2g表示通胀率和经济增长率对M2冲击的响应。从冲击响应波动的整体来看，图4、图5与图3大致相似。从冲击响应的具体变化看，M1供给冲击对通胀率和经济增长率的效应在19个季度后收敛于零，M2供给冲击对通胀率和经济增长率的效应在15个季度后收敛于零。这一结果表明，我国政府为应对全球金融危机而实施宽松货币政策导致的2009Q3—2010Q3的货币供给过剩，对经济增长和通货膨胀的冲击效应持续时间为4—5年。

从冲击响应的方向和持续时间看，m1g和m2g大约在前7个季度为正，表明2009Q3—2010Q3的货币供给过剩对经济增长的正向冲击大约为7个季度，随后m1g和m2g转为负值，并最终收敛于零。另外，m1p和m2p的前两个季度为负，随后转为正值，持续近两年后转为负并收敛至零。上述结果说明，我国以货币供给为标志的货币政策，首先正向作用于经济增长，随后正向作用于通胀。这一结果与我国为应对美国金融危机而实施宽松货币政策，经济增长率先快速触底反弹，而通胀率较后反弹的实际经济背景一致。进一步，图4、图5的结果还表明，如果在2010Q4及以后我国没有明显收紧货币政策或遭遇其他较大幅度的负向冲击，我国宏观经济将在随后一年多的时间里继续保持较高的增长率和通胀率。换言之，在我国2010年11月份CPI同比达到5.1%，以及美联储为刺激经济增长再次推出定量宽松货币政策，向市场注入流动性的情况下，如果我国适度宽松货币货币政策不逐步退出，在随后一定时间内，通胀率和经济增长率将继续攀升。这一结果也为央行在2010年连续6次上调法定准备金率的货币政策提供经验支持。但另一方面，货币供给冲击在大约两年后对经济增长和通胀的效应转为负值。这就说明，如果适度宽松货币政策立即退出，2011年的宏观经济可能出现反复。因此，后金融危机适度宽松货币政策的退出不宜过快，并在退出过程中配合使用积极财政政策，推动技术进步和科技创新，增加有效供给，以此刺激经济增长。

从冲击响应的幅度来看，后金融危机的M1和M2供给冲击对通胀率效应最大值出现在滞后第5季度，响应值为0.72%和0.78%。经济增长率对M1供给冲击响应最大值出现在滞后第4季度，响应值为0.32%；经济增长率对M2供给冲击响应最大值出现在滞后第5季度，响应值为0.79%。由于本文设定的冲击起始点为2009Q3，因此，如果没有继续遭遇货币供给过剩冲击，2010Q3—2010Q4可能是我国经济增长率和通胀率的较高时期，随后可能回落。另外，m1g在滞后第8个季度负值最大，m2g在滞后第10个季度负值最大；对应地，m1P和m2p在滞后第10季度负值最大，由此意味着如果没有宽松财政政策的配合，适度宽松货币政策的退出将使我国宏观经济在2011年底进入局部低谷。但正如前所述，美联储推出的定量宽松货币政策，有可能在一定程度上改变我国未来一定时期货币供给过剩的状况，从而使得我国宏观经济的波动特征变得更为复杂。这就要求我国未来一定时期的货币政策应针对实际宏观经济的运行而灵活、审慎操作。总之，我国货币供给冲击效应的反复波动特征，以及宏观经济面临的较复杂状况，为我国货币政策的操作和调控带来了困难。

本文基于货币过剩法，针对我国货币供给的非线性调节特征，使用阈值协整方法扩展和改进货币需求函数的设定，度量了后金融危机时期的货币供给过剩程度，刻画了不同经济状态下货币供给的非对称调节效果。基于上述结果，进而使用广义脉冲响应函数揭示后金融危机时期，货币供给过剩对通胀与经济增长的冲击效应。

第一，我国的货币供给、总产出、同业拆借利率和通货膨胀之间存在长期均衡的协整关系，由协整关系所确定的货币供给量即为与货币需求相一致的均衡的货币供给量。实际货币供给量高于均衡的货币供给量即为货币供给过剩，实际货币供给小于均衡货币供给即为货币供给不足。从2009Q3开始，我国货币供给出现过剩，且过剩幅度快速增加，其中2010Q3名义M1过剩12.56%，名义M2过剩11.31%。表明现阶段适度宽松货币政策应逐步退出，由协整关系所确定的均衡货币供给量也为我国以货币供给为政策工具的货币政策操作提供参考。

第二，当货币供给偏离货币需求时，货币供给向长期均衡的调节具有非线性。也就是说，当货币供给不足时，货币供给增加的速度相对较快；当货币供给过剩时，货币供给降低增长的速度较慢。这一结果表明央行实施扩张性货币政策较积极，而对紧缩性货币政策的实施较为谨慎。进一步，货币供给向长期均衡的调节对经济增长、通胀的调节效应具有非线性：在货币供给不足时，增加货币供给对通胀、经济增长的刺激效应相对较弱；在货币供给过剩时，减少货币供给对通胀、经济增长的抑制效应相对较强。其引申的含义是，央行在实施货币政策调控时，首先应科学合理地对货币供给状态做出判断，有针对性地实施货币政策，特别是在货币供给不足状态下，货币政策的调节力度应更大；在货币供给过剩时，货币政策操作力度应相对较小。

第三，基于后金融危机时期货币供给的过剩状况及过剩程度，本文设定广义脉冲响应函数研究货币供给冲击对通胀与经济增长的效应。结果表明，后金融危机时期货币供给过剩对经济增长率和通胀率的冲击效应大约会持续4—5年，前两年冲击效应为正，随后转为负。货币供给对通胀与经济增长冲击效应的反复波动说明，现阶段适度宽松货币政策的退出应针对实际经济的运行而灵活操作，并配合积极的财政政策。

参考文献

谢平、罗雄，2002：《泰勒规则及其在中国货币政策中的检验》，《经济研究》第3期。

叶光、张晓峒、聂巧平，2007：《中国货币需求的协整分析和结构VECM估计》，《世界经济》第10期。

王少平、李子奈，2004：《我国货币需求的协整分析及其货币政策建议》，《经济研究》第7期。

伍戈，2009：《中国的货币需求与资产替代：1994—2008》，《经济研究》第3期。

Bae, Y., and Jong, R.M., 2007, “Money Demand Function Estimation by Nonlinear Cointegration”, Journal of Applied Econometrics.22:767—793.

Ball, L., 2001. “Another Look at Long-run Money Demand”, Journal of Monetary Economics, 47:31—44.

Banerjee, A., Dolado, J.J., Galbraith, J.W. and Hendry, D., 1993, Co-integration, Error Correction, and the Econometric Analysis of Non-Stationary Data, Oxford Scholarship Online Monographs.

Beyer, A., 1998, “Modeling Money Demand in Germany”, Journal of Applied Econometrics, 1:57—76.

Calza, A.and Zaghini, A., 2006, “Non-linear Dynamics in the Euro Area Demand for M1”, European Central Bank Series WorkingPaper, Number 592.

Chen, Show-Lin and Wu, Jyh-Lin, 2005, “Long-run Money Demand Revisited: Evidence from a Non-linear Approach”, Journal of International Money and Finance, 24:19—37.

Engle, R.F. and C.W.J. Grangle, 1987, “Cointegration and Error Correction: Representation, Estimation and Testing”, Econometrica, 55:251—276.

Ericsson, N.R., Hendry, D.F. and Prestwich, K.M., 1998, “The Demand for Broad Money in the United Kingdom, 1878—1993”, Scandinavian Journal of Economics, 100:289—324.

Escribano, A. 2004, “Nonlinear Error-Correction: The Case of Money Demand in the United Kingdom（1878—2000）”, Macroeconomic Dynamics, 8:76—116.

Hansen, B.E. and Seo, B., 2002, “Testing for Two-regime Threshold Cointegration in Vector Error-Correction Moldels”, Journal of Econometrics, 110, 293—318.

Haug, A.A. and Tam, J., 2007, “A Closer Look at Long-Run U.S. Money Demand: Linear or Nonlinear Error-Correction with M0, M1, or M2?”, Economic Inquiry, 45:363—376.

Johansen, S., 1995, Likelihood-based Inference in Cointegrated Vector Autogressive Models, Oxford University Press.

Juselius, K.1996, “An Empirical Analysis of the Changing Role of the German Bundesbank after 1983”, Oxford Bulletin of Economics and Statistics. 58:791—819.

Karamé, F. and Olmedo, A., 2002, “The Asymmetric Effects of Monetary Policy Shocks: A Nonlinear Structural VAR Approach”, http://www.univ-orleans.fr/deg/GDRecomofi/Activ/doclyon /karame .pdf.

Koop, G., M.H. Pesaran and S.M. Potter, 1996, “Impulse Response Analysis in Nonlinear Multivariate Models”, Journal of Econometrics, 74:119—47.

Laurence, B. and Mankiw, G., 1994, “Asymmetric Price Adjustment and Economic Fluctuations”, Economic Journal, 104:247—261.

Lütkepohl, H., Teräsvirta, T. and Jürgen W., 1999, “Investigating Stability and Linearity of a German M1 Money Demand Function”, Journal of Applied Econometrics, 14:511—25.

McCallum, B, T. and Goodfriend, M.S., 1988, “Theoretical Analysis of the Demand for Monetary”, Economic Review, 1:16—24.

Museatelli, V.A. and Spinelli, F.,1996, “Modeling Monetary Trends in Italy Using Historical Data:the Demand for Broad Money 1861—1990”, Economic Inquiry, 34:579—596.

Nobay, R. and D.Peel, 2003, “Optimal Discretionary Monetary Policy in a Model of Asymmetric Central Bank Preferences”, Economic Journal, 113:657—665.

Pesaran, H.H. and Shin, Y., 1998. “Generalized Impulse Response Analysis in Linear Multivariate Models”, Economics Letters, 58:17—29.

Polleit, T. and Gerdesmeier, D., 2005, “Measures of Excess Liquidity”, HfB—Business School of Finance ＆ Management Working Paper, No.65.

Sarno, L. 1999, “Adjustment Costs and Nonlinear Dynamics in the Demand for Money: Italy, 1861—1991”, International Journal of Finance and Economics, 4:155—177.

Sim, C., 1980, “Macroeconomics and Reality”, Econometrica, 48:1—48.

Teräsvirta, T. and Eliasson, A., 2001, “Non-linear Error Correction and the UK Demand for Broad Money”, Journal of Applied Econometrics, 16:277—288.

Weise, C., 1999, “The Asymmetric Effects of Monetary Policy: A Nonlinear Vector Autoregression Approach”, Jounal of Money Credit and Banking, 31:85—108.

Wolters, L.T., Teräsvirta, T. and Lutkepohl, H., 1998, “Modelling the Demand for M3 in the United Germany”, Review of Economics and Statistics, 80:399—409.

注释：

①需要说明，使用非线性方法研究货币需求函数已成为近期文献的主流，现有文献的非线性设定包括两个方面：其一是设定协整向量为非线性（Bae and Jong，2007），其二是在误差校正模型中设定非线性。从方法论进步角度看，在货币需求函数的协整方程和误差校正模型中同时引入非线性，可能是货币需求函数研究的未来发展方向。但由于现有计量方法的局限，目前还做不到这一点。鉴于本文的研究目的和我国存在较稳定的线性货币需求函数这一现实，本文使用非线性误差校正模型进行研究。限于篇幅，本文的文献综述中没有提及协整向量为非线性的相关文献。

②由于我国利率是政策性变量，其变动具有一定的刚性，货币供给对其调节效应不显著（王少平、李子奈，2004），因此，这里的误差校正模型没有写出利率的动态调节方程。另外，模型（3）中滞后期L根据AIC准则确定。

③因为B1的第二列就是A1，B2的第二列就是A2，因此，检验Al和A2是否具有显著的差异就转化为检验Bl和B2是否具有显著的差异。

④需要说明的是，使用Hansen ＆ Seo（2002）的方法必须要求模型（2）中的变量具有协整关系，本文使用Johansen（1995）方法检验表明模型（2）中变量具有协整关系。另外，使用Hansen ＆ Seo（2002）的方法对协整方程和后文将要报告的两机制误差校正模型和协整方程是同时估计出来的。为表述方便，本文先报告和分析了协整方程的结果，后报告两机制误差校正模型的估计结果。括号内的数据为对应系数的t统计量。

⑤由微观货币需求理论可知，货币需求是通货膨胀的减函数。原因是通货膨胀具有腐蚀货币购买力的功能，当存在通货膨胀时，人们会更多持有实物资产，而少持有货币。

 

责任编辑：夏雨