会员登录
会员注册内容提要：实际中，越来越多的研究领域所收集到的样本观测数据具有函数性特征，这种函数性数据是融合时间序列和横截面两者的数据，有些甚是曲线或其他函数图像。虽然计量经济学近二十多年来发展的面板数据分析方法，具有很好的应用价值，但是面板数据只是函数性数据的一种特殊类型，且其分析方法太过于依赖模型的线性结构和假设条件等。本文基于函数性数据的普遍特征，介绍一种对其进行分析的全新方法，并率先使用该方法对经济函数性数据进行分析，拓展了函数性数据分析的应用范围。分析结果表明，函数性数据分析方法，较之计量经济学和其他统计方法具有更多的优越性，尤其能够揭示其他方法所不能揭示的数据特征。
关键词：函数性数据 修匀 基函数 函数性主成分分析 函数性方差分析
作者简介：严明义西安交通大学经济与金融学院统计系，西安710048
引言
在传统的统计数据分析中，数据一般具有这样的特征，即数据要么是时间序列数据，要么是横截面数据。而实际中获得的许多统计数据，往往是在时间序列上取多个截面，再在这些截面上同时选取样本观测值所构成的样本数据。计量经济学中称这样的数据为“平行数据”(Panel Data)，也被翻译成“面板数据”，或“纵向数据”(longitudinal data)。近二十多年来，许多学者研究分析了面板数据。事实上，关于面板数据的研究是计量经济学理论方法的重要发展之一，它在解决数据样本容量不足、估计难以度量的因素对经济指标的影响，以及区分经济变量的作用等方面，具有突出优点。但是，研究面板数据的计量经济模型，以线性结构描述变量之间的因果关系，且模型太过于依赖诸多的假设条件，从而使得方法的具体应用及方法适用的数据类型，均具有一定的局限性。为了弥补面板数据的计量经济模型分析方法及其它统计分析方法的缺陷，本文基于统计数据的函数性特征，介绍一种从函数视角对数据进行分析的全新方法一函数性数据分析(Functional Data Analysis, FDA)。
函数性数据分析(Functional Data Analysis,FDA)的概念，始见于加拿大统计学家J.O.Ramsay和C.J.Dalzell 1991年发表的论文《函数性数据分析的一些工具》。近年来，J.O.Ramsay和B.W.Silverman等国外知名统计学者，就函数性数据做了许多研究，也取得了许多有价值的结果。但是，国外在这方面的研究依然处于起步阶段，还有很多问题需要研究或进一步完善；另外，从函数性数据方法应用的领域来看，极少涉及对经济函数性数据的分析研究。国内在此方面的研究，就目前研究文献来看，尚是一片空白。
为填补我国在这方面的研究空白，弥补国际上函数性数据分析在经济领域应用的严重不足，拓展函数性数据分析的应用范围，本文从思想、理论和方法技术等方面，对函数性数据的分析方法进行系统介绍，并通过编写计算机程序，率先利用该方法分析实际的经济函数性数据。
一、数据的函数性特征及函数性数据的例证
（一）数据的函数性特征
一般地说，多元数据分析(Multivariate Data Analysis，MDA)处理的对象，是刻画所研究问题的多个统计指标（变量）在多次观察中呈现出的数据，样本数据具有离散且有限的特征。但是，现代的数据收集技术所收集的信息，不但包括传统统计方法所处理的数据，还包括具有函数形式的过程所产生的数据，例如，数据自动收集系统等。另外，在有些研究领域，获得的样本资料还是曲线或其它函数图像。本文称具有这种特征的数据为函数性数据。
虽然函数性数据的来源形式多种多样，但就其本质来说，它们由函数构成。这些函数的几何图形可能是光滑的曲线（如人体在成年前的身体高度变化等），也可能是不光滑的曲线（如股票综合指数等）。函数性数据分析(Functional Data Analysis,FDA)的基本思想是把观测到的数据函数看作一个整体，而不仅仅是个体观测情的顺序排列。函数指的是数据的内在结构，而不是它们直观的外在表现形式。
实际中，之所以要从函数的视角对数据进行分析是因为：(1)实际中，获得数据的方式和技术日新月异、多种多样，例如，越来越多的研究者可以通过数据的自动收集系统获得大量的数据信息。更重要的是，原本用于工程技术分析的修匀（光滑）和插值(smoothing and interpolation)技术，可以由有限组的观测数据产生出相应的函数表示；(2)尽管只有有限次的观测数据可供利用，但有一些建模问题，将其纳入到函数范式下进行考虑，会使分析更加全面、深刻；(3)在有些情况下，如果想利用有限组的数据估计函数或其导数，则分析从本质上来看就具有函数性的特征；(4)将平滑性引入到一个函数过程所产生的多元数据的处理中，对分析具有重要的意义。
表1陕西第三产业就业人数分类数据（万人）
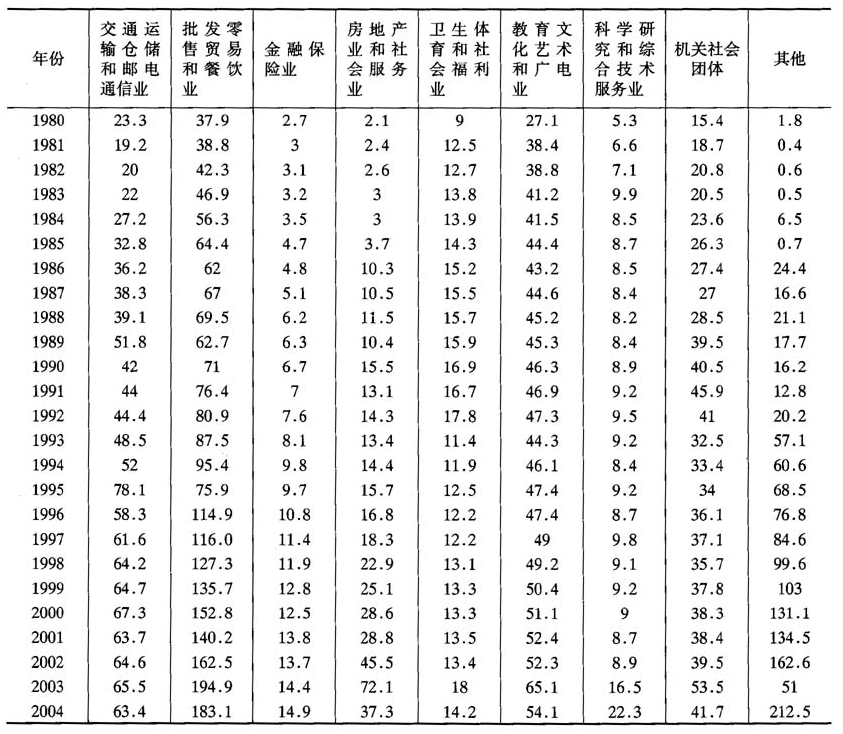
资料来源：历年《陕西统计年鉴》及《陕西五十年》。
（二）函数性数据的例证
在实际的统计数据分析中，函数性数据很常见。例如，如考古学家挖掘的骨块的形状；不同地区的多期温度、降雨量数据；多个地区、行业或企业的多年的年度经济总量；多家商业银行历年的资本结构；不同时间上多个省市的失业数据等。这些统计数据往往呈现函数性特征，即每个个体对应着一个函数或曲线。在对函数性数据进行分析时，将观测到的数据（函数）看作一个整体，而不是一串数字，这是函数性数据分析不同于传统统计分析之根本所在。
表1是陕西省第三产业历年就业人数的分类数据，它将陕西第三产业划分为九类行业。为叙述简单，九类行业从左到右分别记为Case1，Case2，…，Case9，即Case1表示“交通运输仓储和邮电通信业”，其余依次类推。利用基于MATLAB编写的程序，对数据进行修匀处理(smoothing)，并绘出九类行业就业人数的修匀曲线（图1）。由曲线图可以看出，每个个体（行业）对应着一条曲线（其数学表达式为函数），这是将多个行业历年的就业人数记录看作函数的根本理由，也是函数性数据分析的出发点。
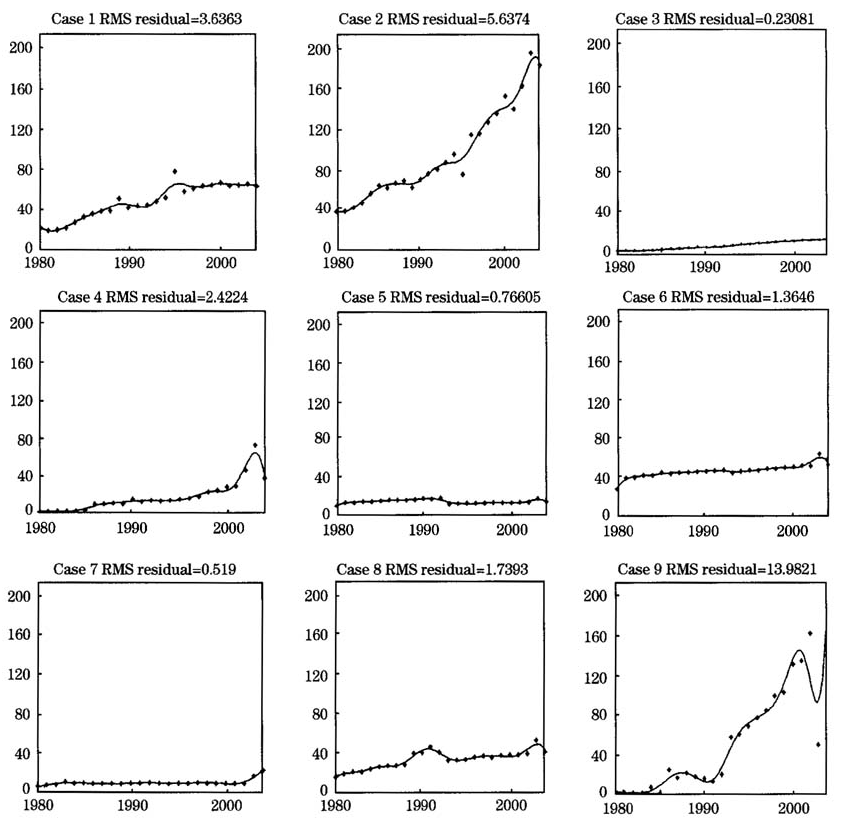
图1九类行业就业人数的修匀曲线
二、从数据的函数性视角研究数据的意义
从函数的视角，对具有函数特征的统计数据进行研究，会挖掘出更多的信息。例如，对函数性数据的修匀曲线展示，不但能够诊断拟合数据的可能数学模型，还能够通过对修匀曲线求一阶或高阶导数，来进一步探索数据的个体（横截面）差异和动态变化规律。
图2是九类行业就业人数的速度（一阶导数）曲线。为了对九类行业就业人数的变动情况能够清晰地展示，在图2中分别以“+”、“·”和“×”特别标注了三类行业，即第二、第四和第九类行业就业人数的速度曲线。观察发现：在1980～2004年期间，九类行业就业人数的变化率差异较大。变化最大的两个行业是第二和第九类行业，即“批发零售贸易和餐饮业”与“其他”两类行业；次之是第一和第八类行业，即“交通运输仓储和邮电通信业”与“机关社会团体”两类行业；期间范围内变化最小的五类行业，是第三、第四、第五、第六和第七类行业，其中第四类行业，即“房地产业和社会服务业”类行业的就业人数，在2001年以后变化较大。
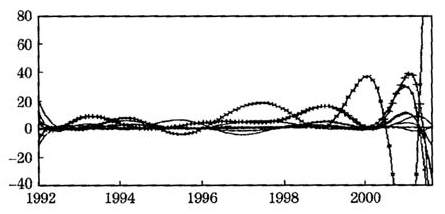
图2九类行业就业人数的速度曲线
进一步，可以绘出就业人数变化率的波动情况，即各类行业就业人数的加速度曲线，结果见图3。图3显示，九类行业就业人数变化率的波动状况不相同，转折变化的时间差异也较大。这些情况一定程度表明，陕西第三产业各类行业，同一时期所处的经济环境不相同，所吸纳的劳动人数的增长变化情况也各不相同。
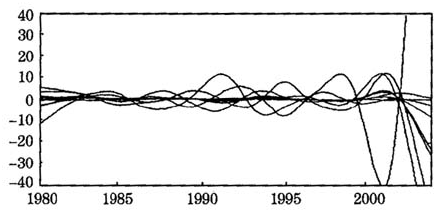
图3九类行业就业人数的修匀加速度曲线
三、函数性数据的初步处理——将离散观测数据转化为函数
实际中获得的数据往往是离散的且只有有限多个，而在一般的函数形式中，已知函数在其自变量（如时间）的取值范围（定义域）内却包含无穷多个值。另外，为了能够进一步反映函数性数据的特征，可能会利用函数的导数（例如前面讨论的就业人数的速度和加速度）。因此，在函数性数据分析中，首要的工作是将观测到的离散数据转化为一个函数。具体地讲，就是利用某次观察的原始数据定义出一个函数x(t)，它在某一区间上所有自变量t处的值都被估算了出来。如果获得的离散数据没有误差，那么
利用基于MATLAB编写的程序，绘出九类行业就业人数的均值函数和标准差函数如图4所示。从中可以看出，随着年份向现在靠近，就业人数的波动程度越来越大。这说明随着时间的推移，经济环境的变化，不同行业吸纳劳动力的能力差异越来越大，并出现了向个别行业“集聚”的现象。
五、函数性数据的变异性分析
（一）函数性主成分分析(functional principal component analysis, FPCA)
关于九类行业的就业人数数据的函数（曲线）展示与初步分析，本文在前面已进行了描述，具体结果见图1～3，概括就业特征的统计量曲线见图4。为了进一步探讨典型函数所呈现的特征，本文利用函数性主成分分析(FPCA)，对就业人数数据进行分析。
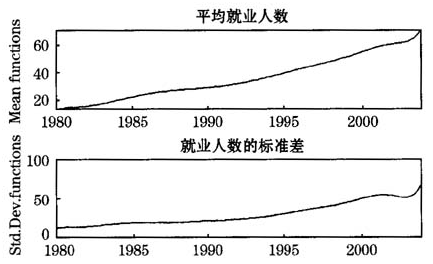
图4九类行业就业人数的均值函数和标准差函数
利用上述方法和基于MATLAB编写的程序，对九类行业的就业数据进行函数性主成分分析(FPCA)。第一个主成分(PC1)的解释能力为86.6%，第二个主成分(PC2)的解释能力为10.5%，前两个主成分的综合解释能力为97.1%。为了清晰地显示主成分，并进行有意义的解释，在同一图中绘出三条曲线，一条是总体均值曲线，另两条是对均值曲线分别加上和减去主成分的一个适当倍数而形成的曲线，具体结果见图5（本文所选的倍数是30）。以上所述的三条曲线分别对应着图中的实心曲线、“+”曲线和“-’油线。PC1反映了1980～2004年期间就业人数的一般变化水平，PCI得分越高，说明就业水平越高于平均水平。图5表明，1993年以后的PCI得分远离平均值，反映了就业人数的“近期”变化情况（1993年以后）。PC2体现了就业人数的一种变动方式，以前高于平均水平的就业水平，而后回落低于平均水平；以前低于平均水平的就业水平，而后回升高于平均水平，反映了就业水平的一种“交错”变化。进一步，可求出九类行业的PC1和PC2得分，并绘出它们的得分情况见图6。图中的交通、批发、金融、房地、卫生、教育、科研、机关和其他，分别对应着九类行业。
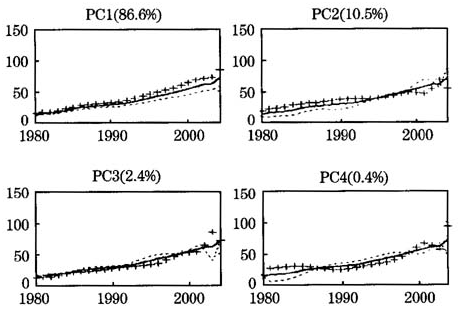
图5主成分偏离均值函数的效应图
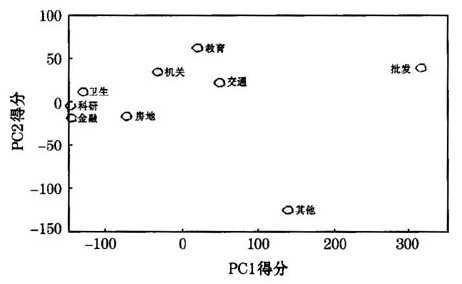
图6九类行业的PC1和PC2得分图
（二）函数性方差分析(functional variance analysis)
为了说明函数性方差分析的应用，本文将陕西第三产业的九类行业分为三个类别，一个类别由第三、第四、第五和第七类行业组成，即图6中金融、房地、卫生、科研构成的类别；第二个类别由第一、第六和第八类行业组成，即图6中的交通、教育、机关构成的类别；第三个类别由第二和第九类行业组成，即图6中的批发、其他构成的类别。通过编写程序及计算，得出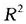
(t)函数曲线及F比率曲线图，见图7。从
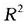函数及F比率图可以看出：1993年以后，除过2003年，
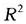几乎都超过0.88，模型与函数性数据拟合的很好；F在1992年以后，除过2003年，均大于临界值5.14（显著水平为0.05），这说明1992年以后（除过2003年），陕西第三产业的就业人数在三个类别上有显著的差异。
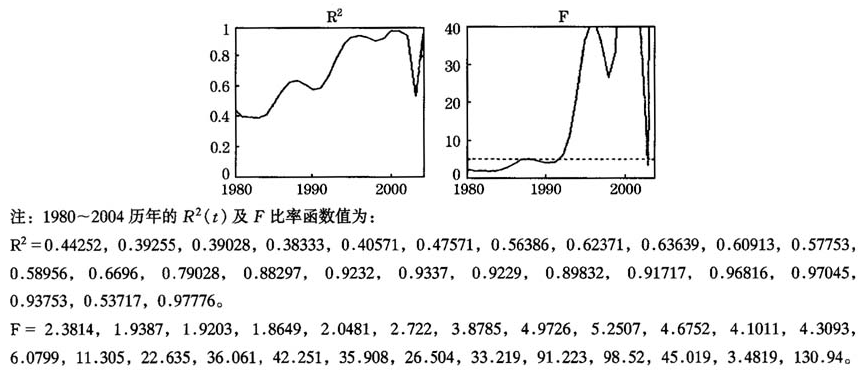
图7平方复相关函数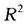
(t)和F-比率函数曲线
六、函数性数据分析的目标和步骤
通过以上对函数性数据分析的理论描述和实例研究，可以发现函数性数据分析的目标与传统统计学分析的目标基本一样，即以对进一步分析有利的方法来描述数据；为突出不同特征而对数据进行展示；研究数据类型的重要来源和数据之间的变化；利用输入（自变量信息）解释输出（因变量）的变化情况；对两组或更多的某种类型的变量数据进行比较分析。
为了在实际中更好地应用本文介绍的方法，对函数性数据进行分析，本文给出典型FDA的基本步骤如下：
第一步，原始数据的收集、整理和组织。假设我们考虑的自变量是一维的，记为t，一个t的函数仅在离散抽样值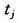
(j=1,2,…,n)处被观测，而且这些
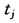可能等间隔分布，也可能不是。在函数性数据分析中，将这些离散的观测值看作一个整体。
第二步，将离散数据转换为函数形式。
第三步，多种形式的初步展示与概括统计量。概括统计量包括均值和方差函数、协方差与相关系数函数、交叉协方差(cross-covariance)与交叉相关(cross-correlation)函数等。
第四步，为了使每一条曲线的显著特征都在大体相同的自变量处（如月份、年份等）显现出来，可能需要对函数进行排齐(registration)，其目的是能够区别对待垂直方向的振幅变化与水平方向的相变化。
第五步，对排齐后的函数性数据进行探索性分析，如函数性主成分分析(FPCA)、函数性典型相关分析(FCCA)等。
第六步，建立模型。建立的模型可能是函数性线性模型，也可能是微分方程。
第七步，模型估计。
七、结论
实际中，越来越多的领域所收集的样本观察资料是曲线或图像，即函数性数据。因此，对这种类型的数据进行统计分析和描述，具有重要的现实意义。因篇幅所限，还有一些函数性数据的分析方法未予以介绍和应用，如函数性典型相关分析及描述动态性的微分方程等。由于本文的主要目的，是通过对函数性数据分析方法的具体应用，传述对数据进行分析的新思想，而不只是方法技术本身。因此，缺少的方法并不影响对思想的阐述与理解。
另外，本文对陕西第三产业就业人数的分析，例证了函数性数据的分析方法，具有传统统计分析方法不可比拟的优越性，具体表现在：(1)通过对函数性数据的修匀，将一阶或多阶导数，如速度和加速度，引入到分析过程中。这一点在计量经济学和多元统计的分析方法中未予以考虑；(2)函数性数据分析，用最少的假设来研究曲线间和曲线内部的结构变化。关于这一点它优于计量经济学中处理“面板数据”的方法。事实上，面板数据只是函数性数据的一种类型，本文介绍的数据分析方法可用来处理许多领域的函数性数据，应用范围相对宽广，而且观测时点也可以不等间隔选取；(3)将数据曲线的振幅变化与相位变化分开处理，是函数性数据分析的一个中心理念，但在以前的分析中却被忽视了。
虽然，关于函数性数据的研究，已经取得了一些成果，但国际上对该方法的研究还只能算刚刚起步。因此，还有很多问题有待更深入地探讨和进一步完善，但愿本文能抛砖引玉，引发更多更好的统计数据分析思想和方法的推出。