会员登录
会员注册作者简介：陈学彬上海财经大学贸易经济系
AD-AS模型（总需求——总供给模型）是现代西方经济学中重要的宏观经济理论模型，是分析市场经济社会总量失衡问题及客观经济波动问题的重要工具，在西方国家被广泛应用。AD-AS模型原理在近年我国经济理论分析中已获初步应用。本文根据AD-AS模型基本原理，结合我国实际进行修改和补充的基础上建立的AD-AS动态仿真模型，将一般的AD-AS几何图形模型转换成为能够实际运算的代数方程模型。并利用它对我国改革以来的宏观经济运行轨迹进行了历史仿真检验和未来运行动态模拟分析。在将AD-AS模型实用化方面进行了初步的尝试。
一、模型结构
本文建立的我国AD-AS动态仿真模型由价格调整方程（总供给方程的变形）、价格预期方程、总需求方程、货币供给增长率控制方程、货币流通速度变化率方程、潜在总产出方程和其它辅助方程构成。模型涉及到如下变量：m为货币供给增长率、v为货币流通速度变化率，q为总需求增长率，Q为实际GNP，Q[＊]为潜在GNP，q[＊]为潜在GNP增长率，p为价格上涨率，pt为价格预期，PO为价格稳定目标，ma为货币供给增长率调控参数。
模型假定我国改革以来的宏观价格波动主要是由总供求失衡前一季度供求状况决定，仿真间隔因此定为0.25年（1个季度）。
模型各方程的表达式及其含义如下：
1.价格总水平波动方程
价格总水平波动方程又称价格调整方程。它反映价格总水平随供求平衡状况和价格预期、价格冲击的变化而上下波动的情况。它是总供给方程的变形。其基本表达式为：
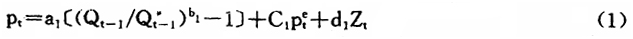
可见，该方程由供求平衡状态影响项、价格预期影响项和价格冲击影响项组成。该方程与附加预期的菲力普斯曲线方程：
十分相似。
式中，π为通货膨胀率，π[e]为通货膨胀预期，Y为实际GNP，Y[＊]为潜在GNP，Z为价格冲击，f为参数。它们都由供求影响、价格预期和价格冲击项组成。但不同的是，附加预期的菲力普斯曲线方程描述的是总供给曲线。该曲线为在Y[＊]点截距为π[e]+Z，斜率为f的直线。而本模型所用价格波动方程描述的曲线为在Q[＊占截距为cp[e]+dZ的抛物线。它正确的描述了总供求失衡状况对价格总水平和实质总产出的非对称影响：当存在衰退性缺口时，总需求变动对总产出的影响大于对价格总水平的影响；当存在膨胀性缺口时，总需求变动对价格总水平的影响大于对总产出的影响。显然这比将其描述为线性关系更为接近实际。
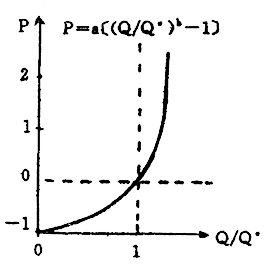
图1供求状况对价格的影响
不过利用式(1)描述现代社会价格总水平与总供求关系时还须做一些调整。该式的供求影响项：
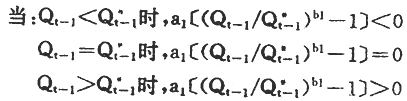
这表明，经济衰退时，价格下降；经济膨胀时，价格上涨；供求平衡时，价格不变。其图形如图1所示。它对我国60年代的宏观经济和价格波动的描述和对美国等西方国家七十年代以前的宏观经济和价格波动的描述是基本正确的。那时伴随经济衰退的确是价格总水平的绝对下降（如图2所示）。
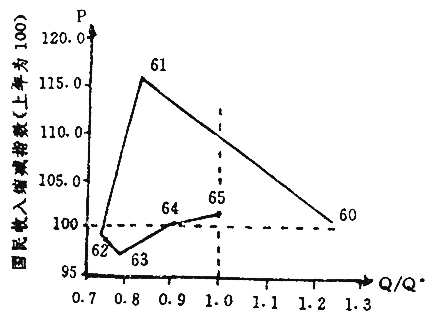
图2我国60年代经济与价格波动
但在我国改革开放以来宏观价格波动的一个新特点是价格只涨不跌。伴随经济衰退的只是价格上涨率的下降而不是价格水平的下降。如图3所示，在Q/Q[＊]=1点，P不是等于零，而是大于零约3-7个百分点。特别是在80年代后期，即使Q/Q[＊]＜1，P仍较大幅度地大于零。总供给曲线向左上方移动。这里即使考虑价格预期P[e]和价格冲击Z的影响，式(1)仍不能很好地描述这种波动轨迹。因此，有必要对该式作一修正。通过对我国79-93年宏观经济和价格波动轨迹的数值模拟，发现该式应修改为以下形式才能较好地描述其运行动态。
|
式中：1979＜t＜1989a[,1]=0.015 1988＜t＜1994a[,1]=0.030 b[,1]=15,c[,1]=0.4,d[,1]=1 |
当Q/Q[*]=1时，a[,1](Q[,t-1]/Q[*,t-1])[b1]=a[,1]。它说明在供求平衡时，即使价格预期p[e]和价格冲击Z为零，价格上涨率也不等于零，而是等于a[,1]值。1979-1988年期间a[,1]约等于0.015，1978-1993年期间a[,1]约等于0.03。在供求总量平衡时，价格总水平仍然上涨的原因，除了价格预期和价格冲击等原因外，很重要的一个原因是在价格刚性作用下，供求结构失衡使供过于求部分商品价格不能下降，或下降幅度不能抵销供不应求部分商品价格上涨的影响所致。
2.价格预期方程
本模型的价格预期方程为修正的综合性预期方程：
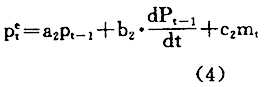
该方程由前期价格变动影响项a[,2]P[,t-1]和前期价格变动加速度影响项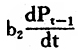
货币供给影响项c[,2]m[,t]构成。这既不同于货币学派代表人物弗里德提出的适应性预期方程（P[e,t]=a[,1]P(,t-1)+a[,2]P[,t-2]+…+a[,n]P[,t-n]，也不同于理性预期学派提出的理性预期方程。
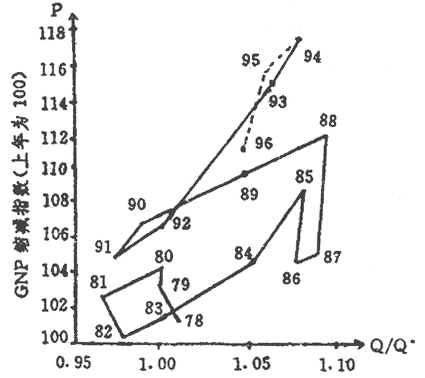
图3我国改革以来的经济与价格波动
人们的价格预期通常首先是根据前期价格变动率做出的。因此，价格预期方程的基本项为a[,2]P[,t-1]。这是一种适应性预期，是一种被动的滞后预期。但人们还会根据价格变动率的变动趋势（加速度）来修正自己的预期。价格变动率的微分反映了这种加速度。当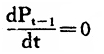
时，表明前期价格上涨率趋于稳定，他会以前期价格上涨率的某一比值修正本期价格预期。当
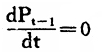时，表明前期价格呈现加速上涨的趋势，人们必然预期价格上涨将进一步加速，t期价格预期必大于前期价格上涨率。当
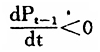时，表明前期价格上涨率呈现下降的趋势，人们通常预期价格上涨率将进一步降低，t期价格预期必小于前期价格上涨率。因而，这种预期已不是一种简单的适应性预期，而是一种理性预期。因而大大地缩短了预期的滞后期，降低了其被动性。
但这种理性预期并不同于理性预期学派的理性预期。后者认为理性人能够作出和政策制定者整齐划一的预期。如价格加速上涨时，它预期政府将采取紧缩政策，从而价格上涨率必然下降。这样，他们预期的价格上涨率的下降幅度与政府实行紧缩政策后的价格上涨率的下降幅度必然相等。这种预期与实际价格变动之间不存在时滞。而本模型的价格预期与现实价格变动的时滞尽管比纯粹的适应性预期有所降低，但一定量的时滞总是存在的。特别是在价格变动出现转折点时，这种预期的时滞和误差均会加大。因为，在t-1期价格变动加速时，人们尽管预期政府会采取措施抑制价格上涨，但一方面这些措施的效果是不确定的，另一方面其作用效果的实现也有一定时滞，所以大多数的人宁愿在看到实际价格上涨速度开始稳定或减速后而不是之前调整自己的预期。本模型中的价格预期方程能够较好地反映这种预期变动。
3.总需求方程
实质总需求为名义总需求除以价格水平。如以货币流通量(M)和货币流通速度(V)之乘积表示名义总需求，则实质总需求(Q)为：
由于我们在考察宏观经济和价格波动时，重点关心的是其变化率而非绝对水平。因此，我们应将以上总需求方程转换为总需求变化率方程。通常采取微分方法推导其变化率方程：
对(5)式取对数：lnQ=lnM+lnV-lnP
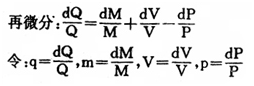
则：q=m+v+p
式中：q为实质总需求增长率；m为货币流通量增长率；v为货币流通速度增长率；p为价格总水平增长率。
该方程的变形：m=q+p-v即理论界通常使用的货币供给增长率方程。该方程在经济理论和实际部门有广泛的应用。但是，这一采用微分方法推导的变化率方程有一严重缺陷：微分方法假定变量是连续的，数据观测时间间隔趋于无穷小。但实际经济统计资料是离散的，观测时间间隔并非趋于无穷小。在每一观测时间间隔内被测量变化较小时，应用微分方法推导的变化率方程计算，误差尚小。如1982年我国m[,0]=10.79%；v[,0]=-1.8%；p[,0]=0.5%，代入(6)式，q=0.1079+(-0.018)-0.005=0.0849，当年GNP实际增长率为8.8%，误差仅0.31个百分点。该式还是可用的。
但当一观测间隔内被测量变化较大时，该方程的计算则会出现较大的误差。如1988年，m[,0]=46.72%；v[,0]=-15.16%；p=11.85%。代入(6)式，q=0.4672+(-0.1516)-0.1185=0.1971，而当年GNP实质增长率为11.3%，误差值为8.4个百分点，误差率为74.4%。，显然，具有如此大误差的方程是不能在本模型中使用的。不过，我们可以采用专门用于处理离散时间变量的差分方法来推导总需求增长率方程：
上式即为用差分方法推导的总需求增长率方程。将1982年和1988年数据代入：
|
q[,82]=〔0.1079+0.1079×(-0.018)+(-0.018)-0.005〕/(1+0.005)=0.0876 q[,88]=〔0.4672+0.4672×(-0.1516)+(-0.1516)-0.1185〕/(1+0.1185)=0.1129 |
这与该两年的实际数值已基本相等，误差已降到相当小的程度。其原因在于差分方法没有变量连续的要求，这与经济统计实际更为吻合。因此，本模型将采用该方程作为实质总需求增长率预测方程。加上时间下标，该方程为：
|
qt=(m[,t]+m[,t].v[,t]-p[,t])/(1+p[,t])(8) |
为便于将经济波动与价格波动进行比较分析，模型选择GNP增长率和GNP缩减指数作为衡量经济波动和价格波动的指标。货币供给增长率作为外生变量，由中央银行货币政策控制。图4是我国改革以来M[,0]和M[,2]增长率与GNP缩减指数关系图。从中可见，M[,0]和M[,2]增长率均与价格总水平波动之间均有较强的相关性。但M[,0]比M[,2]的相关性更高。显然，选用M[,0]作为模型控制变量比M[,2]能更好地反映我国改革以来这段过渡时期货币供给变动与价格波动的关系。究其原因，主要是我国现阶段的银行信用仍不够发达，现金交易在商品交易中所占比重仍较高并有上升趋势。如1979年M[,0]占M[,2]的比率为16.65%，1988年上升到23.32%，1993年仍达20.15%。
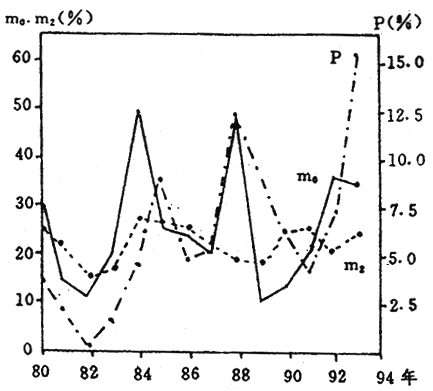
图4我国m[,0]·m[,2]与GNP缩减指数变化动态
4.货币供给增长率控制方程
货币供给增长率在模型中作为政策控制变量，在历史仿真期间根据历史数据外生输入；在对未来政策仿真时，采用以下比例调节方程控制：
|
m[,t]=m[,t-1]·〔1+ma(PO[,t-1]/p[,t-1]-1)〕 |
式中：
m[,t]为货币供给增长率；
ma为货币供给增长率调控参数；
PO为稳定价格目标。
模型假定，宏观货币政策以稳定价格总水平为首要目标。因此，货币供给增长率的调节主要以前期价格上涨率与稳定价格目标的差比作为调节货币供给增长率的依据。这是一种反馈调节，具有一定的滞后性。当仿真间隔DT增大时，时滞增大，DT减少时，时滞缩小。它表明货币当局需经常地根据经济运行状态信息调节货币供给量。ma作为调控参数，可供政策试验时进行各种调控力度之动态效果的模拟。
5.货币流通速度变化率方程
在总需求增长率方程中，货币流通速度变化率(v)是一重要的组成项。它的预测精度直接影响到总需求增长率的预测精度。
表1我国1980-1993年v[,0]变化率模拟值单位：%
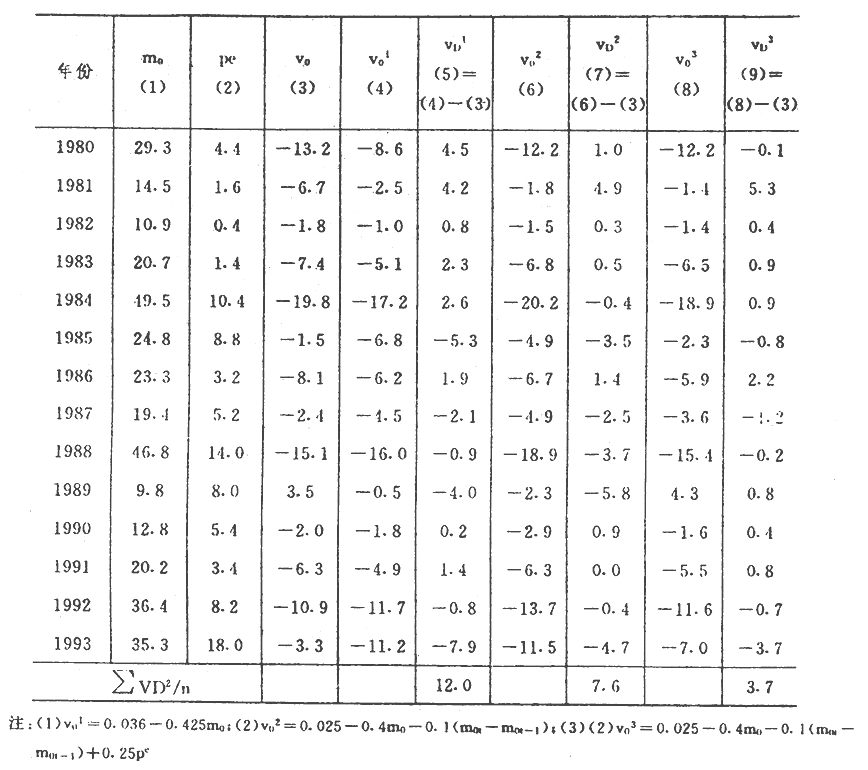
西方著名的货币学派在分析货币供给对经济增长和价格变动的影响时，通常把V看成是一个常数，或把它看作一个具有稳定变化趋势的变量。然而我国的货币流通速度V[,0]并不是一个常数，而是一个具有下降趋势的变量。从1979年的14.9次降到1993年的5.4次，下降63.8%，年均下降7.5%。这种下降趋势主要是由我国经济货币化进程决定的。而且这种下降速度并非常数，而是一个剧烈波动的变量。其波幅为(-19.84)-3.5%，达23个百分点。这样的波幅对总需求增长率的影响是巨大的。因而是不能忽略不计的。
我们的分析表明，货币流通速度变化率V[,0]与货币供给增长率m[,0]之间存在极强的负相关关系。以1980-1993年数据回归，回归方程V[,0]=0.036-0.425m[,0]，相关系数r=-0.864。m[,0]每增加1%，V[,0]大约降低0.425个百分点。货币流通速度变化率与货币供给量增长率反向变动，实际起到了减缓货币供给变动对价格和产出冲击的作用。如1988年m[,0]增长46.72%，V[,0]降低15.16%，减少货币供给大幅增长的冲击作用约22.42个百分点(46.72%×(-15.16%)+(-15.16%)。1989年m[,0]猛降为9.84%，给经济带来极大的紧缩冲击，这时V[,0]反降为升，加速3.5%，减轻了货币供给增长率大幅下降的冲击作用。利用1980-1993年数据拟含方程(v[,0]=0.036-0.425m[,0])对该时期v[,0]进行仿真检验结果如表1所示。拟合值基本能够反映v[,0]的变动趋势，其均方差为0.12，但最大误差为0.079，超过1个百分点的有9项，且误差较大额均发生在货币供给增长率变动较大的年份。这说明货币流通速度变化率不仅与货币供给增长率有关，而且还与其加速度有关。以m[,0]和m[,0]加速度进行拟合得：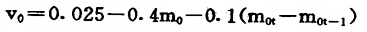
。据此进行仿真检验，误差大大缩小，均方差降为0.076，最大误差为0.058，但超过1个百分点的误差项仍达8项。而最大误差项仍出现在货币供给增长率突然大幅增加或减少年份。这又是价格剧烈波动的年份。显然v[,0]的变动还与价格预期相关。人们预期价格将加速上涨时，会加速抢购商品，从而加速货币流通；反之，当人们预期价格将下降时，人们会持币待购，从而降低货币流通速度。货币流通速度与价格预期成正比。考虑三者影响的货币流通速度变化率方程为：
|
v[,0]=0.025-0.4m[,ot]-0.1(m[,ot]-m[,ot-1])+0.25p[e](9) |
其模拟值及误差如表1第8、9栏所示。模拟精度大幅度提高，均方差猛降到0.037，超过1个百分点的误差项降为4项。可见，式(9)较好地模拟了我国改革以来货币流通速度的变化动态。因此，本模型将采用该方程作为货币流通速度变化率方程。
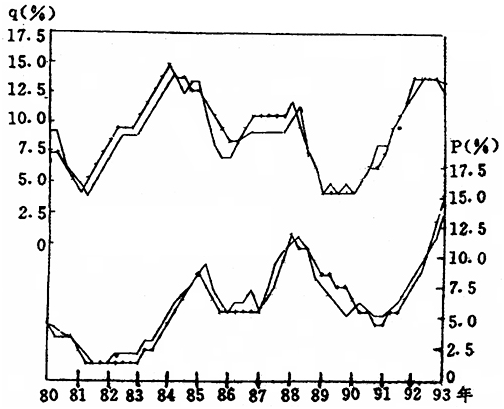
图5对我国改革以来经济与价格波动的模拟检验
6.潜在产出方程
潜在产出是一个国家的生产要素获充分利用时的产出水平。受生产要素稳定增长的制约，潜在产出在中长期内通常呈现出一种稳定增长的趋势。在统计上它通常表现为中长期平均增长趋势线。因此，本模型采用中期年平均增长率乘上年产出的方法计算每年的潜在产出：
Q[*,t]=Q[*,t-1]·q[*,i] (10)
式中：Q[*,t]为t年潜在GNP；q[*,i]为i期GNP平均增长率。
受多种因素的制约，在不同时期的潜在产出增长率是不同的。我国改革以来潜在产出的增长大致分为两个阶段：1979-1983年为第一阶段，GNP年均增长率为7.8%；1984-1993年为第二阶段，GNP年均增长率为9.2%。本模型分别以其作为各阶段的潜在GNP增长率。
二、模型检验
利用1979-1993年我国宏观经济和价格波动的数据对模型进行了模拟检验。模型参数如表2所示，模拟检验的主要指标如表3所示。
表2模型方程及其参数
注：dt为仿真间隔，等于0.25年。
表3对我国改革以来经济与价格波动的模拟检验
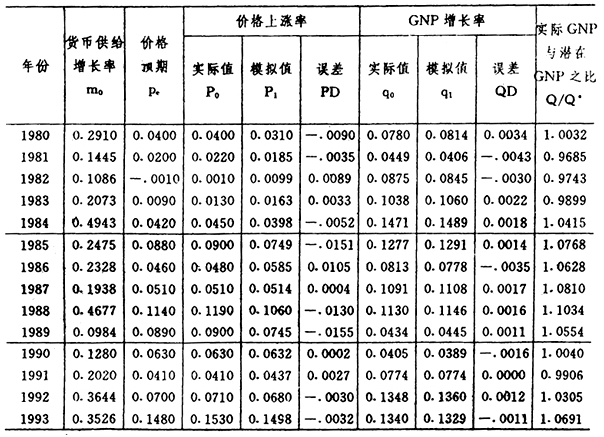
从表3和图5可见，该模型在以实际货币供给增长率作为输入变量的条件下，较好地模拟了我国改革以来十多年的GNP增长率和GNP缩减指数的变化动态，具有较好的模拟特性。因此，我们可以用它进行宏观经济理论和政策效果的模拟分析，为理论研究和政策制定提供较为丰富和准确的定量分析依据。
从模型参数估计和模拟运行中我们发现，价格波动方程的参数a在1980-1993年的历史仿真期间取同一参数值会给模拟值带来较大误差。而分段在1980-1989年取值0.015，1990-1993年取值为0.030，则能大大地缩小其误差，获得较好的模拟效果。这一参数值差别意示着，在1980-1989年期间，供求缺口为零时的价格上涨率为1.5%；而1990-1993年，则上升为3%，增加1倍。同期供求平均状况对价格总水平上涨率的推动也提高一倍。这说明随着我国经济体制改革的深化，价格的进一步放开，市场价格与市场供求状况的联系更加紧密。在价格刚性作用下，更高的经济增长伴随着更高的价格上涨。
三、模型的初步应用
本文建立的宏观经济模型，可用于宏观经济理论和政策效果的动态模拟分析。本文主要设计了三种相机选择。逆向调节货币供给增长方案和三种稳定货币供给增长方案进行初步的模拟分析。
逆向调节方案假定，货币供给总量控制是宏观经济调控的主要手段，政府主要通过调节货币供给总量的方法来实现抑制宏观经济和价格剧烈波动的任务。方案以价格上涨率控制目标(PO)作为模型内生调控货币供给增长率的依据。三个方案均假定今后十年以10%的价格上涨率作为控制目标，并分别以0.3、0.2和0.1作为模型自动控制货币供给量增长率的调节参数(ma)，模拟不同货币供给调控力度的动态效果。
稳定货币供给增长方案假定，中长期货币供给增长率为一常数。模拟目的在于与逆向调节方案相结合，比较稳定的货币供给增长与不断变化的货币供给增长的动态效果和稳定的不同货币供给增长率的动态效果。本文设计了30%、25%和20%三种稳定的货币供给增长方案进行模拟。
从以上几种方案模拟结果的比较中可见：
1.稳定的货币供给增长是抑制宏观经济和价格剧烈波动的重要条件。
尽管货币供给稳定增长的三个方案的经济增长率和价格上涨率均不同，但其共同的特点却是经济增长和价格波动都较为迅速地趋于稳定。而相机选择，频繁变动货币供给增长率的三个方案的共同特点却是经济和价格的周期性波动，尽管其波动幅度和波动周期相关较大。在相机选择政策下，调控力度越大（调节参数ma的值越大），货币供给增长率逆向变动幅度越大，经济和价格波动幅度越大，波动周期越短；反之，则波动幅度越小，波动周期越长。
方案1-1的货币供给调节系数为0.3，货币供给增长率m[,0]波动幅度为18个百分点，GNP增长率和价格总水平上涨率波动幅度约7个百分点，波动周期约5年。方案1-2的货币供给调节系数为0.2，m[,0]波幅降为9个百分点，q和p波幅降为4.5个百分点。方案1-3的货币供给调节系数降为0.1，m[,0]波幅降为4个百分点，q和p波幅降为2个百分点，并趋于稳定。可见，稳定的货币供给增长政策是抑制宏观经济和价格剧烈波动的重要保证。从改革十多年的历史经验来看，货币供给增长率数次剧烈波动，波幅近40个百分点，这是同期经济和价格剧烈波动（波幅近10个百分点）的重要原因之一。因此，我国经济要实现持续稳定增长的目标，成功地避免和抑制宏观经济和价格的剧烈波动，首先必须避免货币供给增长的剧烈波动，实行较为稳定的货币供给增长政策。
2.稳定的货币供给增长率的高低，主要影响价格上涨水平，而较少影响经济增长水平。
从稳定货币供给增长的三个方案可见，尽管其货币供给增长率每个方案相差5个百分点，但三个方案的GNP增长率在2000年均逼近于10%。相差不到0.5个百分点，而价格上涨率每个方案相差约4个百分点，分别逼近于11.7%、7.5%和3.5%。而10%的GNP增长率正是模型设定的九十年代中后期到二十一世纪初期的潜在GNP增长率。当改变该潜在GNP设定值，则各方案GNP增长率模拟值以相同比例变动。可见，在稳定货币供给增长条件下，实际GNP增长率是由潜在GNP增长率决定的。潜在GNP增长率是由特定时期的生产力增长速度决定的，而不是由超过生产力增长速度所需要的货币供给增长所决定的。因此，试图以增加货币供给的办法来刺激经济持续增长是徒劳的。它仅会带来价格总水平的持续上升。
3.不断变动的货币供给增长不仅影响价格变动，也影响经济增长，但其对经济增长的刺激作用是短暂和有限的，而其恶果却是经济和价格的剧烈波动。
从相机选择、逆向调节的三个方案可见，货币供给与经济增长之间的确存在正相关关系。货币供给增长加速，经济增长也加速；货币供给增长减速，经济增长也减速。但是，货币供给变动对经济增长的刺激作用是短暂的和有限的。货币供给增长不能不断加速。不断加速增长的货币供给只会带来经济的崩溃——恶性通货膨胀。货币供给增长一旦停止加速，它对经济增长的刺激作用就会消失。货币供给增长趋于稳定，经济增长也将趋于稳定并逼近于潜在产出水平。
因此，不断变动的货币供给增长尽管对价格和产出均产生影响，因而成为在需求膨胀、经济过热时紧缩需求，抑制经济过热和价格急剧上涨的重要手段；在需求不足，经济萧条时刺激需求，刺激经济增长的重要手段。但切不可过度使用。否则必然造成经济和价格的剧烈波动。
4.我国货币供给增长率m[,0]中长期应稳定在25-30%之间。
从以上几个方案的模拟结果可见，我国货币供给增长率m[,0]稳定在25-30%之间是较好的。20%的m[,0]增长方案尽管可使价格上涨率稳定地下降到3-4%，但因其货币供给增长低于经济发展的需要，使经济增长率长期低于潜在产出水平，因而是不可取的。25%方案在使GNP增长率稳定在10%左右的同时，使价格水平（GNP缩减指数）稳定在7.5%左右，可作为货币供给增长率的下限。30%方案使经济增长率略高于25%方案的同时，使价格上涨率稳定在11.5%左右，可作为货币供给增长率控制的上限。m[,0]最大波幅控制在5个百分点之内，经济增长率可稳定在10%左右，价格上涨率可稳定在9%左右，经济运行轨迹可能如图方案1-3的小幅波动。这可能是一种比较理想的经济运行状态。
5.近期经济应继续实行适度从紧，少量收缩的政策。
从1991年开始的本次经济和价格波动周期，价格上涨约比经济上涨滞后一年，经济增长在1992年达峰顶，1993年维持一年，1994年已开始下降。价格上涨在1994年才达峰顶，滞后近两年。主要是前期经济持续高涨，膨胀性缺口进一步扩大和通胀预期加大所致。由于时滞作用，1995年初价格上涨仍将继续维持较高水平，随后将逐步回落。因此，1995年应继续实行适度从紧，少量收缩的政策，应避免为追求价格上涨率的大幅下降而使货币供给紧缩过度，造成经济增长的大幅滑坡。因此，1995年的货币供给增长率m[,0]应控制在28-30%之间，以使经济增长率稳定地回落到8.5-10%的水平，价格上涨率可回落到15%左右。1996年将m[,0]控制在28%左右，经济增长率可稳定在8-9%，价格上涨率可回落到10%左右。1997年货币供给适当放松，经济将开始在较高水平上的回升，价格上涨率仍可维持在10%左右。此次经济和价格波动周期可如方案1-3较为平稳地结束。
注释：
(1)罗伯特·E·霍尔，约翰·B·泰勒，《宏观经济学——理论、运行和政策》中译本，中国经济出版社，1988年。
(2)罗伯特·E·小卢卡斯，《关于产量与通货膨胀的替换关系的某些国际性证明》，《美国经济评论》，第63卷，1973年。
(3)米尔顿·弗里德曼，《货币政策的作用》，《美国经济评论》，1968年3月号。
(4)陈学彬，《价格宏观调控论》，四川大学博士学位论文，1994年。