会员登录
会员注册4.当ε＜0时，广义Pareto分布“厚尾”性分析
当ε＜0，β＞0时，其定义域为0≤y≤-β/ε，广义Pareto分布为“截尾”分布，如图7、图8所示。由于是“截尾”分布，当超阈值充分大时，其尾部分布概率密度函数值为零。此时相对“拖尾”分布的正态分布，必为“薄尾”分布。
若0＜y＜2β/(1-ε)时，得到H'(z)＞0。由于z＜0，于是有H(z)＜H(0)=0。此时，超阈值所服从的广义
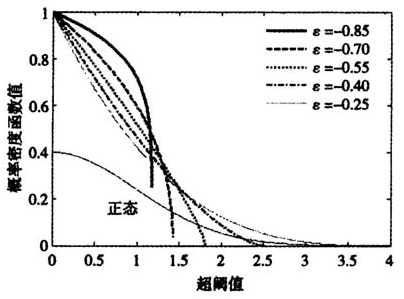
图7-1≤ε＜0，β＞0时广义Pareto分布的“厚尾”性
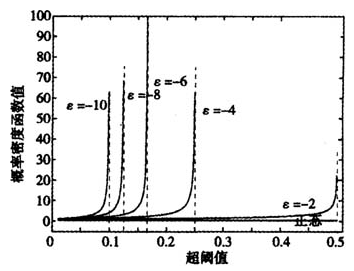
图8ε＜-1,β＞0时广义Pareto分布的“厚尾”性
Pareto分布的尾部随形状参数的增加而变薄。将上述条件和定义域合并，得到：
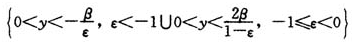
若y＞2β/(1-ε)时，得到H'(z)＜0。由于z＜0，于是有H(z)＞H(0)=0。此时，超阈值所服从的广义Pareto分布的尾部随形状参数增加而变厚。将上述条件和定义域合并得到：
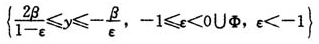
将上述两种情况按形状参数ε分别归纳如下：
当-1≤ε＜0，由(3)式和定义域知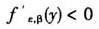
，此时超阈值所服从的广义Pareto分布的概率密度函数为减函数。若0＜y＜2β/(1-ε)时，超阈值所服从的广义Pareto分布的尾部随形状参数的增加而变薄。而此时若2β/(1-ε)≤y≤-β/ε时，尾部随形状参数的增加而变厚。
为实证的需要，取β=1，ε取-0.85～-0.15之间，间隔为0.15的五个值，用MATLAB7.0绘得广义Pareto分布概率密度函数如图7所示。其中(2β/(1-ε),-β/ε)依次为(1.0811,1.1765)，(1.1765,1.4286)，(1.2903,1.8182)，(1.4286,2.5)，(1.6,4)。上述结论得以验证。
当ε＜-1时，由(3)式和定义域知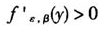
，此时超阈值所服从的广义Pareto分布的概率密度函数为增函数。若0＜y＜-β/ε时，超阈值所服从的广义Pareto分布的尾部随形状参数的增加而变薄。
为实证的需要，取β=1，ε取-10～-1之间，间隔为2的五个值，用MATLAB 7.0绘得广义Pareto分布概率密度函数如图8所示。其中-β/ε依次为0.1,0.125,0.167,0.25,0.5。上述结论得以验证。
5广义Pareto分布“厚尾”性分析
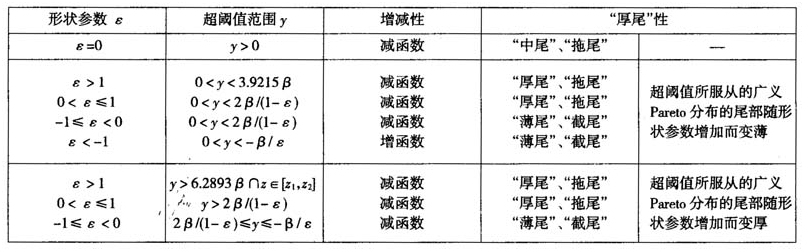
根据上述分析，超阈值所服从的广义Pareto分布概率密度函数的增减性及分布的“厚尾”性总结如表1所示。
由表1知：①当形状参数ε=0、ε＞0、ε<0，对应的广义Pareto分布分别为“中尾”、“拖尾”分布，“厚尾”、“拖尾”分布和“薄尾”、“截尾”分布。②当ε＜-1时，广义Pareto分布的概率密度函数为增函数，除此之外的其他情形均为减函数。③当ε＞1时，广义Pareto分布为“厚尾”分布，但其尾部随形状参数的增加变化规律难以确定。④POT模型中的广义Pareto分布尾部随形状参数的变化更为具体和多样，更适合金融风险度量。综合以上分析理论后得出，当且仅当0＜ε≤1，y＞2β/(1-ε)时，分布为“厚尾”分布，概率密度函数递减且尾部随着形状参数的增加而变厚，变厚的速度越来越慢。股票和高频外汇回报的实践中通常满足0＜ε≤0.5，此时最适合于金融资产时间序列“厚尾”分布建模。
表1超阈值近似服从的广义Pareto分布的“厚尾”性(β＞0)
三、POT模型用于金融风险度量
POT模型用于金融风险度量中阈值的选取很重要，过高不能满足估计需要的样本量，过低又不能满足分布的“厚尾”特征。选取阈值的常用方法是超阈值均值函数的线性法则。超阈值均值函数e(u)定义为C(X-u|X＞u)。当超阈值服从广义Pareto分布时，超阈值均值函数为(β+ε·u)/(1-ε)，是线性函数。实践中，选取不同阈值计算样本超阈值均值，得到样本超阈值均值函数(SMEF)图，记为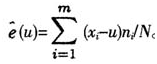
。理论和实践表明，超阈值服从广义Pareto分布的样本超阈值均值函数图形在阈值以上的部分为正斜率的直线，以此来选取超阈值。
广义帕累托分布参数估计最常用的方法是极大似然估计，通常包括点和区间估计，前者是估计的基础，后者是为避免过高的估计线性误差所设计，用似然比检验得到。除参数的极大似然估计外，还有其他方法，如概率加权矩估计，分布函数的线性（Kearns和Pagan, 1997）或非线性回归估计等。
给定一组符合渐近广义Pareto分布的超阈值样本，根据渐近广义Pareto分布的分布函数得到相应的概率密度函数和对数似然函数为：
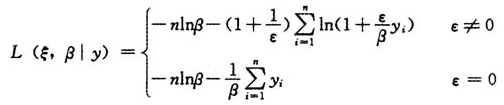
Hosking和Wallis(1987)曾证明，当ε＞-0.5时，满足极大似然估计的正则条件，此时参数的极大似然估计量服从非对称正态分布，估计量的渐近标准误差可以通过极大似然估计相应得到。
联合(1)式和(2)式并在正确估计阈值和计算样本超阈值的基础上估计超阈值渐近广义帕累托分布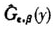
。于是，超过该阈值的金融资产回报尾部分布函数估计（封建强，2002；陈守东等，2007）为：
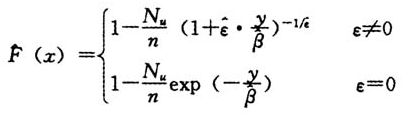
给定置信水平1-p的上分位点，即VaR的估计（封建强，2002；陈守东等，2007）为：
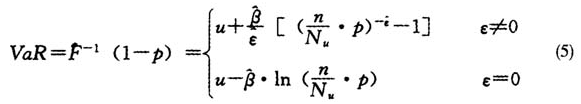
假如一项资产在一年内超过某个最大损失（如上式所示）的概率为P，在L年内的损失情况为L重贝努利(Bernoulli)试验。令X为上述事件第一次发生所需的年数，则它服从参数为P的几何分布，X的期望值为1/P。意味着L年内某项资产第一次超过某个最大损失平均需要1/P年。因而可用k=1/P年事件和对应的最大损失来度量某一极端事件发生的频率和资产的风险。
四、实证研究结果统计分析
作者从中国期刊网上查询到应用POT模型度量金融资产市场风险的主要参考文献，表2和表3（见下页）列举了其中6篇文献。文献中所取样本主要包括上证指数和深圳成分指数以及汇率高频数据等。由于10多年来我国股市在不断发展、制度在不断健全、市场在逐渐规范，投资者也渐趋理性，股份行为必然会表现出明显的阶段性。因而在样本选取上多数考虑到了1996年12月16日前后的股份行为的差异。文献中所取股市样本区间为1990年12月19日至2007年6月26日之间不等。上证A股指数（部分）收盘价如表3所示。其中汇率区间为1971年1月4日至2003年5月30日。
研究使用的收益率指标是日对数回报，定义为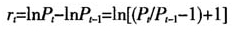
，其中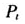
为股指在t时的收盘价，
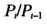即为日百分比收益率。在估计VaR时，一般对日对数收益率取负号，通过计算得到的上侧分位数取负号即为所测度的风险值。
表2GPD“厚尾”性用于金融风险测度的实证统计的样本
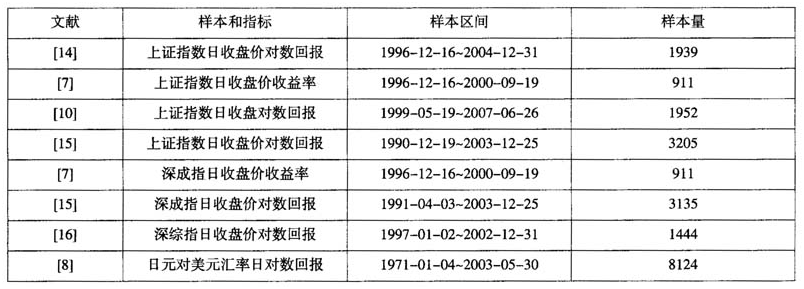
表3上证A股指数的日收盘点数(2007-06-26～2007-04-11)
注：原始数据来源于国泰安研究服务中心http://www.gtarsc.com/Login.aspx.
根据本文第三部分的理论所述，选取阈值及相应的超阈值个数如下页表4所示。ε和β参数估计可直接借助SPLUS软件得到，或者在极大似然估计中，将极大化似然函数转化为二元函数无条件极值问题，用MATLAB命令fminunc和fminsearch予以实现。在此基础上，根据公式(5)可算出不同显著性水平下的VaR值。结果如表4所示。
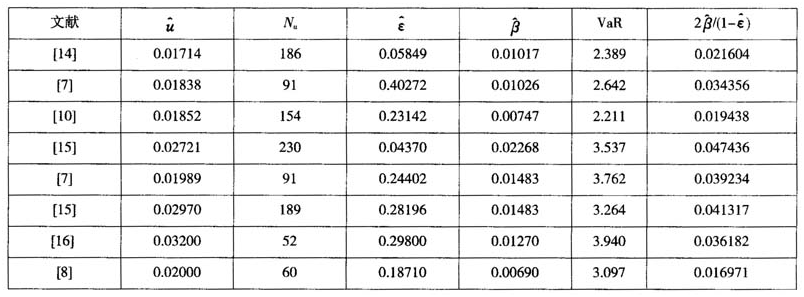
表2中文献及表4的实证研究结果表明：①股票和高频外汇回报的超阈值拟合广义Pareto分布，得到形状参数ε估计的最大值为0.40272，最小值为0.04370，平均为0.21843。可见，通常它们都属于0＜ε≤0.5范围内，满足0＜ε≤1的条件。较大的超阈值一般较多，因此由理论部分得到的0＜ε≤1，y＞2β/(1-ε)条件得以满足。此时最适合于金融资产时间序列“厚尾”分布建模和参数的极大似然估计。②[7]、[10]、[14]、[15]四篇文献中，上证指数对应GPD的形状参数估计分别为0.40272、0.23142、0.05849和0.04370，其平均为0.184083。在95%的置信水平下，上证指数风险度量VaR值分别为2.642%、2.211%、2.389%和3.537%，平均数为2.695%。[7]、[15]、[16]三篇文献中，深圳成分指数对应的形状参数分别为0.24402、0.28196、0.29800，平均数为0.27466。在95%的置信水平下，深圳成分指数的风险度量VaR值分别为3.762%、3.264%和3.940%，平均数为3.655%。在同一文献[7]中，上证指数的风险度量VaR值为2.642%，深圳成分指数的风险度量VaR值为3.762%。可见，深圳证券市场收益率分布尾部明显厚于上海证券市场。深圳证券市场比上海证券市场包含更高的市场风险。③我国从1996年12月开始实行涨跌停板制度（柳会珍等，2006）。从上海证券市场来看，制度执行后的[7]、[10]、[14]三篇文献的VaR平均值为2.414，制度执行前后的文献[15]的VaR值为3.537。可见，该制度执行后市场风险明显下降，该制度有效地控制了股票市场的投机现象，从而降低了投资者的收益损失风险。深圳证券市场这一特征不甚明显。
表4GPD“厚尾”性用于金融风险测度的实证统计的参数估计
五、结论
通过上述研究得出的结论有：①传统研究将POT模型用于具体的金融风险度量的实践中，只是回答了在具体领域中如何应用的问题。本文为POT模型用于金融风险度量的依据进行科学论证，回答了为什么可以去用的问题。同时，通过实证研究的统计分析既证明了论证的合理性并得出我国沪深股市及汇率市场风险特征的一些新结论，因而具有更为重要的理论和实践意义。②当形状参数ε=0，ε＞0和ε＜0时，对应的广义Pareto分布分别为“中尾”、“拖尾”分布，“厚尾”、“拖尾”分布和“薄尾”、“截尾”分布；当ε<-1时，广义Pareto分布的概率密度函数为增函数，除此之外的其他情形均为减函数；当ε＞1时，广义Pareto分布的尾部随形状参数的增加变化规律难以确定；POT模型中广义Pareto分布的尾部随形状参数的变化更为具体和多样，更适合金融风险的度量；当且仅当0＜ε≤1，y＞2β/(1-ε)时，分布为“厚尾”分布且尾部随着形状参数的增加而变厚，而股票回报和高频外汇回报中通常0＜ε≤0.5，此时POT模型最适合于金融资产时间序列“厚尾”分布建模。③可用k=l／P年事件和对应的最大损失，即VaR来度量某一极端事件发生的频率和资产的风险。④我国金融市场大量的实证研究结果表明，股票和高频外汇回报的超阈值拟合广义Pareto分布的形状参数通常都属于0＜ε≤0.5范围，与理论研究结论相一致。此时最适宜金融风险度量和参数的极大似然估计。⑤深圳证券市场收益率分布尾部明显厚于上海证券市场，深圳证券市场比上海证券市场包含更高的市场风险。可见，上海证券市场相对深圳证券市场表现更为成熟；自1996年12月，股市涨跌停板制度执行后市场风险值VaR明显下降，表明该制度执行有效地控制了股票市场的投机现象，从而降低投资者的收益损失风险。⑥在上述研究的基础上，考虑多种金融产品交易的组合，可以利用多元极值理论进行分析，目前该领域已取得一些重要成果并成为国内外研究热点，相信极值理论在多金融领域中有着更为广阔的应用前景。
参考文献：
[1]Coles, S., An Introduction to Statistical Modeling of Extreme Values[M], Springer-Verlag UK, 2001:119～136.
[2]J. Pickands., Statistical Inference Using Extreme Order Statistics[J], The Annals of Statistics, 1975,3:119～131.
[3]Zajdenweber., Extreme values in business interruption insurance[J], Journal of Risk and Insurance, 1996,63:95～110.
[4]Mcneil., Estimating the tails of loss severity distributions using extreme value theory[J], Astin Bulletin, 1997,27:117～137.
[5]Resnick., Discussion of the Danish data on large fire insurance losses[J], Astin Bulletin, 1997,27:139～151.
[6]刘国光等：《沪深股市收益分布尾部特征研究》[J]，《数理统计与管理》2005年第3期。
[7]封建强：《沪深股市收益率风险的极值VaR测度研究》[J]，《统计研究》2002年第4期。
[8]高松、李琳：《平稳序列的POT模型及其在汇率风险价值中的应用》[J]，《系统工程》2004年第6期。
[9]Dupuis D., Estimating the probability of obtaining non-feasible parameter estimates of the generalized Pareto distribution[J], Journal of Statistics Computation and Simulation, 1996, 54:197～209.
[10]桂文林：《上证股指极值模型估计和VaR计算》[J]，《数学的实践与认识》2008年第19期。
[11]Gilli M., Extreme values theory for tail-related, risk measure[C], Computation Finance 2000 Conference, 2000:9～11.
[12]Comnel-Brizio H F, Hernandez-Montoya A R., On fitting the Pareto-Levy distribution to stock market index data: selecting a suitable cut off value[J], Physica A, 2005,354:437-449.
[13]王炳兴：《Pareto分布中门槛值的确定及其在股票市场中的应用》[J]，《数理统计与管理》2008年第6期。
[14]陈守东、孔繁利、胡铮洋：《基于极值分布理论的VaR与ES度量》[J]，《数量经济技术经济研究》2007年第3期。
[15]欧阳资生、龚曙明：《广义帕累托分布模型：风险管理的工具》[J]，《财经理论与实践》2005年第137期。
[16]柳会珍、顾岚：《股票收益率分布的尾部行为研究》[J]，《系统工程》2005年第2期。
[17]柳会珍、顾岚：《金融市场极端日收益数据的广义Pareto分布拟合》[J]，《数理统计与管理》2006年第6期。