三、实证分析
现有医疗保险中的损失数据9200个,本文利用这组数据建立数据文件,并利用这组数据在MATLAB中进行损失数据分布拟和。
(一)初步分析
在把数据导入到MATALAB中后,首先给出数据基本统计信息如下:
Min 118
Max 331359
Mean 9701.4
Median 6969
Kur 162
Skewness 8.89
从上面的统计结果可以看出:损失数据的最小值为118,最大值为331359。显然,所有的损失数据都是正值,而且最大值和最小值相差很大,最大值是最小值的2808倍,平均值为9701,中位数为6969,由于中位数不易被极端值影响,所以,中位数比均值稳健。可以看出均值大于中位数,显然,均值收到了右端的一些较大值的影响。峰度为162,偏度为8.89,峰度用于度量样本数据偏离某分布的情况,正态分布的峰度为3,当样本数据的曲线峰值比正态分布高时,峰度大于3;反之,比正态分布低时,峰度小于3。偏度用于衡量样本均值的对称性,若偏度为负,则数据均值左侧的离散性比右侧的强;若偏度为正,则数据均值右侧的离散性比左侧的强。正态分布的偏度是零。从上面的统计描述结果可以看出,损失数据是一个高峰、拖尾的在正半轴的分布,具有典型的非寿险损失分布的特点。
下面,利用公式(4)在MATLAB中编程,计算经验平均超出函数,在这里需要注意的一点是在对损失数据进行排序后会发现一些数据值重复的情况,对于这些数据在本文中采用了只保留一个数据的做法,这会造成一定的信息损失,但是,由于多数重复损失数据在分布在数据值很小的部分,利用平均超出函数主要关注的是损失数据的“尾部”特性,此外,这样作也可以减少编程的复杂性,因此,在这里采用这种作法是可行的。在计算得到经验平均超出函数之后,作出相应的散点图如图1。
从经验平均超出函数的散点图的变化趋势来看,大约当x的取值大于60000后, 的变化趋势趋于明显上升但并不是很稳定。通过对图1和图2的对比,可以初步断定损失数据可能服从对数正态分布或者帕雷托分布。损失数据关于对数正态分布和帕雷托分布的q-q图,如图3、图4。
的变化趋势趋于明显上升但并不是很稳定。通过对图1和图2的对比,可以初步断定损失数据可能服从对数正态分布或者帕雷托分布。损失数据关于对数正态分布和帕雷托分布的q-q图,如图3、图4。
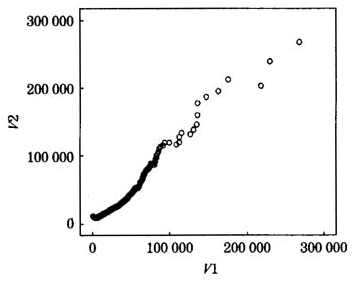
图1经验平均超出函数散点图
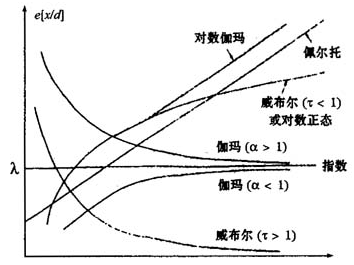
图2平均超出函数图
注意到图3、图4的纵坐标轴长度并不相同,帕类托分布q-q图的纵轴的长度是对数正态分布其q-q图长度的2倍,对比两个图形可以看出,经验损失数据与对数正态分布的更为接近。因此,通过以上分析,可以决定损失数据服从对数正态分布族。
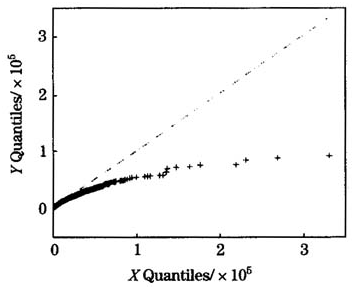
图3对数正态分布q-q图
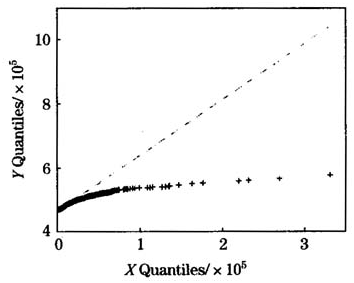
图4帕雷托分布q-q图
(二)参数估计
精确的参数估计方法有三种,一种是极大似然估计法,第二种最小距离法,第三种是矩方法。矩方法涉及求解方程组的数值解,由于本问题的数据量比较大,考虑到计算机效率和计算精度问题,我们这里并不采用矩方法。最小距离法很容易理解,但是其统计特性并没有极大似然估计好,所以,本文考虑使用极大似然估计来进行参数估计,利用MATLAB得到以下结果:

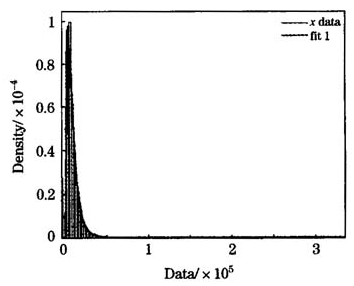
图5对数正态分布拟和图
从上面的MATLAB极大似然估计结果看出,参数估计mu=8.88,sigma=0.72;参数估计的标准误分别为0.00752009和0.00531794,这样小的标准误表明参数估计的很好。在此参数估计结果下的拟和图见图5。
从图5可以看出,除了实际损失数据的尖峰高于拟和的对数正态分布外,在上面估计参数的结果下,对数正态分布很好的拟和了损失数据,特别是损失数据的尾部。
(三)检验
在上文中已经通过极大似然估计得到了对数正态分布族的参数估计,但参数估计所得到的结果仅仅是在事先选定的分布族中,哪一个具体分布距离损失数据的总体最近,正如在数据的初步分析的q-q图和经验平均超出函数散点图中看到的,损失数据服从哪种分布类并不明显,因此并没有十足的把握认为损失数据的总体就一定属于对数正态分布族。实际上,从区分损失数据的剩余经验图来看,损失数据总体也有可能属于帕雷托分布族,因此,我们必须对我们认为损失数据总体来自对数正态分布族的判断进行检验。
利用MATLAB编写程序得到以下结果(部分结果):

我们在检验中将整个损失数据划分为六个区间,划分区间依次为:(0, 5000),(5000,7000),(7000,9000),(9000,14000),(1400,23000),(23000,inf)。之所以这样划分区间是为了保证在卡方检验中使得每个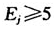 ,以保证卡方检验的效果。求得卡方统计量为:chisum=1.415874762348426e+002。
,以保证卡方检验的效果。求得卡方统计量为:chisum=1.415874762348426e+002。
在90%的置信系数下,MATLAB给出的临界值为:
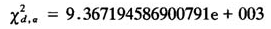
由于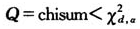 ,所以,在10%的显著性水平下不能拒绝原假设,即,我们认为损失数据总体是服从参数为mu=8.88,sigma=0.72的对数正态分布的。
,所以,在10%的显著性水平下不能拒绝原假设,即,我们认为损失数据总体是服从参数为mu=8.88,sigma=0.72的对数正态分布的。
四、结语
本文从对给定的损失数据的描述统计分析开始,到损失分布类选择、参数估计、模型检验等过程,结合实际的医疗损失数据进行了系统、全面的理论方法论述,对于非寿险这种通常要具体问题具体分析的损失数据分布拟和给出了一套完整、清晰、科学的基于计算机实现的思路。与此同时,文章强调了MATLAB在分布类选择。参数估计等方面的强大功能,并给出了适当的编程思路。对于文章中出现的损失数据重复的问题,还有待于进一步研究更加科学的方法。
参考文献:
[1]张博.精算学[M].北京:北京大学出版社,2005.
[2]谢志刚,韩天雄.中国精算师资格考试用书—风险理论与非寿险精算[M].天津:南开大学出版社,2001
[3]王晓军.保险精算学[M].北京:中国人民大学出版社,1999.
[4]王新军.财产保险业发展趋势与科学厘定费率问题研究[J].山东财政学院学报,2002,(6).
