二元经济中城乡混合基尼系数的计算与分解（一）

内容提要：关于基尼系数计算方法的文献已经十分丰富，但专门计算城乡混合基尼系数的理论方法，却一直没有得到很好的解决，这导致全国收入分配长期变化方面的某些研究难以深入。本文建立了城乡混合基尼系数的新算法，并给出新的分解形式，同时还提出并论证了度量城乡差距的新指标。该分解形式具有明确的经济含义和理论意义，并且不依赖于“城乡收入分布不重叠”的假定。利用这一分解形式的经济含义，我们分析了几个重要理论问题。最后，应用新算法计算并分解了中国个别年份的城乡混合基尼系数，以检验新算法的有效性。
    关键词：城乡混合基尼系数 混合基尼系数分解形式 城乡收入分布相对差距指数
    作者简介：程永宏 中国人民大学公共管理学院社会保障研究所
    

        引言
    中国经济直到目前仍然具有典型的二元结构特征，其主要表现之一就是：在城乡之间存在着显著的收入水平和收入分布的差异。对于这种经济，由于技术上和理论上的原因，计算城乡混合基尼系数（注：城乡混合基尼系数是指，把全国所有城镇和农村居民看作一个整体，按全部国民收入在这一整体中的分配状况所计算的基尼系数，这里定量描述全国收入差距的重要指标，有些文献称之为“全国基尼系数”。）非常困难。
    如果基于城乡混合的收入调查数据，利用通常的几何法或平均差法等进行计算，这在理论上是可行的。国内曾有学者在个别年份进行过这种调查和计算，例如，李强等(1995)、赵人伟和李实(1999, p.49)等。但这种方法的广泛应用遇到几个难题：首先因为过去多年中国统计部门一直没有进行过城乡混合的收入调查，因而这种方法不能满足研究中国收入分配历史变化过程的要求；更重要的是，根据城乡混合的收入调查数据，无法对城乡混合基尼系数进行分解分析，这对于研究全国收入差距的构成及其变化是一个重大损失。
    而利用城乡分离的收入调查数据计算城乡混合基尼系数，这在目前的国内外文献中都没有得到很好的解决（胡祖光，2004；李实、赵人伟，1999；李实，2000；李强、洪大用等，1995）。
    胡祖光(2004)根据《中国统计年鉴》中独立的城镇和农村居民收入调查资料，对通常的人口等分法进行修正，即把农村最贫穷的33.3%人口视为城乡混合后全国最贫穷的20%人口，把城镇人口中最富的50%视为城乡混合后全国最富的20%人口，其依据在于：前者平均收入低于同期城镇居民困难户的平均收入。这种处理作为一种近似方法是可行的，但从理论上看，即使农村最贫穷的33.3%人口平均收入低于城镇困难户的平均收入，但农村人口中的高收入仍然有可能超过城镇人口中的低收入；事实也的确如此（董静、李子奈，2004）。这种情况会导致上述方法失效。
    陈宗胜、周云波(2002,p.26-29)给出一个“分层加权法”计算公式，并计算了中国1988-1998年的城乡混合基尼系数。该算法把城乡人口分组数据中各组人口比重的加权平均，等同于全国人口分组数据中的各组人口比重，这种等量关系是否严格成立，需要进一步讨论。
    一些关注基尼系数可分解性的文献对计算城乡混合基尼系数具有重要参考价值，但遗憾的是，这些分解形式存在很强的约束条件。例如Sundrum,R.M(1990,p.50)提供了一种算法，用来计算由“穷人”和“富人”两个群体构成的混合群体的基尼系数：设“穷人”群体的基尼系数、平均收入、人口比重分别为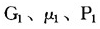，“富人”群体的基尼系数、平均收入、人口比重分别为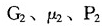，全体人口的平均收入设为μ，则混合群体的基尼系数G可分解为为：
    附图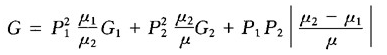
    国内有学者引用这一公式计算中国城乡混合基尼系数，这就忽略了这一算法所需要的一个很强的条件：穷人与富人的收入分布不重叠。这在现实经济中是很难满足的，例如，1995年，中国农村居民中就有26%高于城镇居民中最低10%收入组的平均收入（李实，2002）。因此，严格说来，Sundrum的算法不适合计算城乡混合基尼系数。
    针对这一问题，董静、李子奈(2004)对Sundrum的算法进行了修正，以便更合理地用来计算城乡混合基尼系数。从其证明过程看，这一修正的算法依赖于“城镇和农村居民的收入是两个服从正态分布的独立随机变量”这一假定，但现实经济中居民收入不一定服从正态分布。
    Cowell(2000)总结其他学者的研究成果时指出：混合群体的基尼系数无法在不同群体之间分解尽净，因为混合基尼系数除了要包括各组内部差距之外，还应包括组间差距和交叉项，即：
    附图
    徐宽(2003)对过去八十年中基尼系数计算方法（包括分解方法）的发展进行了一次全面总结，从中可以看出，到目前为止，基尼系数按组群分解的方法主要就是上述这种形式，并且其中的交叉项颇有争议：Mookherjee and Shorrocks(1982)等认为它不可能有精确解释；Silber(1989)和Lambert andAronson(1993)则认为它有明确的经济意义，并给出了一个解释，但这个解释实质上也只是说：交叉项反映了各组收入分布的重叠程度，除此以外并没有更多的经济含义。
    综上所述，到目前为止，城乡混合基尼系数的计算及分解一直没有得到满意的解决。
    本文根据笔者以前提出的一种单一样本基尼系数计算方法（程永宏、糜仲春，1998），构建了一种理论上可靠的城乡混合基尼系数计算方法，并给出一种全新而且简单的分解形式。
    为了清楚地阐述本文算法的原理，这里有必要部分地重复笔者此前推导一般基尼系数计算方法的过程，本文第二部分主要是完成这一工作，并对这一算法的误差进行估计；第三部分导出城乡混合基尼系数的计算公式；第四部分对城乡混合基尼系数进行分解，并在此基础上建立了全面度量城乡差距的新指标；第五部分应用本文的算法，计算了1990年中国城乡内部基尼系数和城乡混合基尼系数，以检验本文算法的有效性；第六部分对本文算法的优缺点进行了总结。
    一、用收入分布函数计算单一总体的基尼系数G
    本文以基于个人收入的基尼系数为例论证新算法的原理，其他类型基尼系数的算法同此。
    (1)洛伦兹曲线与收入分布函数的解析关系：
    在一个人数众多的收入总体中，个人收入可以被近似地看作一个连续型随机变量I，因此，个人收入分配状况可以用随机变量I的概率分布函数来表示，即：

P{I

    上式的含义是：收入不大于t的人数占全体居民总数的比重是F(t)。从洛伦兹曲线的定义可知，洛伦兹曲线与个人收入分布函数存在确定的关系，因此，可以考虑通过个人收入分布函数导出洛伦兹曲线表达式。厉以宁、秦宛顺(1997)提到了二者的解析关系；程永宏、糜仲春(1998)也曾经以不同方式推导出这一关系；
    附图
    在现实经济中，由于远大于1，F(0)左右极限应该非常接近，二者之差可以忽略不计；F(T)的左右极限也是如此，故可以把(10)和(12)式代入(9)式，得到：
    附图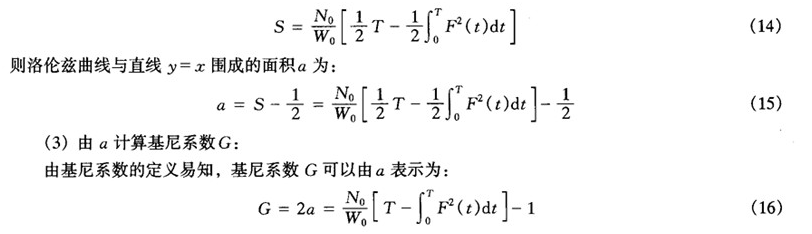
    这就得到利用收入分布函数计算基尼系数的基本公式。该式与Kendall and Stuart(1977)、Dorfman (1979)、Yizhaki(1982)和Lambert(1989)等得出的结果及其推导方法（徐宽，2003）都不同，但可以证明，这几个结果都是等价的。利用这一公式计算基尼系数还需要解决三个问题：收入分布函数的具体形式、全体居民中最高收入者的收入T和全体居民总收入。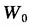
    第一个问题可以利用一个合适的概率分布函数拟合收入抽样调查数据得到解决。
    第二个问题可以利用已知的收入分布函数合理地“外推”出最高收入T得到解决，即由(13)式中F的表达式解出T值：
    附图
    这样获得的“最高收入”基本上真实反映了收入分布的实际趋势。
    第三个问题可以由(4)式解决。因为，全体居民总收入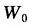实际上就是累积收入W在t=T时的值，因此，由(4)式得到：
    附图
    至此，我们利用洛伦兹曲线与收入分布函数的解析式，导出了计算基尼系数的一般方法，但这一公式只适合单一总体的抽样调查数据。本文第三部分将以此为基础，解决利用城乡分离的收入数据计算城乡混合基尼系数的问题。
    

（未完待续）