二元经济中城乡混合基尼系数的计算与分解（三）

四、对本算法的检验——根据统计数据计算并分解中国的城乡混合基尼系数
    为了检验上述算法的有效性和可操作性，我们利用1990年中国城乡收入分组数据计算并分解当年城乡混合基尼系数。计算过程主要包括以下几个步骤：
    (1)根据城乡收入调查数据，拟合城乡家庭人均收入分布函数。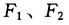
    根据1990年的统计资料，我们分别采用城镇家庭人均生活费收入和农村家庭人均纯收入分组数据，计算出各收入水平下城乡家庭人均收入分布频率（见表1）。
    表11990年中国城镇和农村家庭收入分组数据
    附图
    数据来源：根据《中国统计年鉴1991》（国家统计局，1991,p276、294）相关收入分组数据计算。
    接下来的关键在于高精度地拟合收入分布函数，这需要找到适当的概率分布函数形式。我们试用了帕累托函数、伽马函数，正态分布函数等，发现都不适合中国城乡收入分配状况；经过反复试验对比，最终发现，对生物学中常用的逻辑斯蒂函数稍加变形，用来拟合中国城乡收入分布比较适合，只是在两端理论曲线比实际分布上升稍快，为此，我们将自变量t的指数由1降为0.05，拟合效果得到极大改善。因此，最终选定以下函数形式拟合中国城乡收入分布：
    附图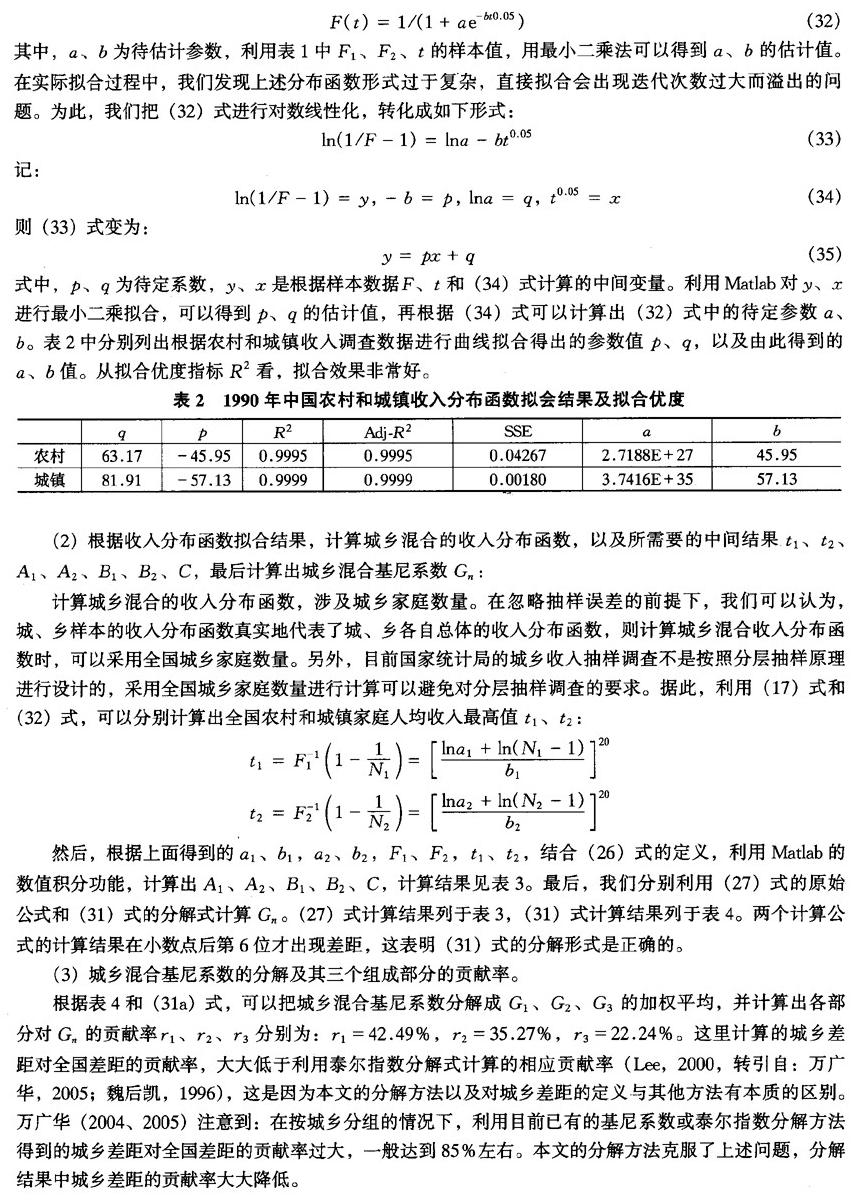
    表3利用(27)式计算城乡混合基尼系数
    附图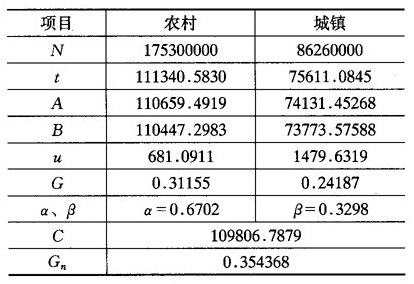
    注：表中u是指“全国城镇或农村家庭人均收入的平均值”。
    数据来源：这里的农村和城镇家庭数量根据《中国统计年鉴1991》（国家统计局，1991）中农村和城镇家庭平均人口(p276、294)以及农村和城镇总人口 (p79)计算；α、β根据计算。
    表4利用(31)式计算城乡混合基尼系数
    附图
    注：这里，农村收入份额，而不等于农村居民收入总和占全国城乡收入总和的比重，其中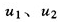，分别为农村和城镇家庭人均收入平均值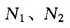；分别为全国农村和城镇家庭数量。这是因为，这里的基尼系数是以家庭人均收入而不是个人收入为基础进行计算的；“城镇收入份额”也是同样定义的。
    数据来源：根据《中国统计年鉴1991》相关数据计算。
    五、总结
    从上述论证过程和检验结果看，本文构建的城乡混合基尼系数计算方法是可靠的，并在以下几个方面获得了一些新的结果：
    第一，建立了计算并分解城乡混合基尼系数的新方法，这一方法无需进行分层抽样调查。
    第二，建立了全面度量城乡差距的新指标。
    第三，本算法给出的混合基尼系数分解形式，不依赖于“城乡收入分布不重叠”的假定。
    第四，本算法可以避免通常算法低估基尼系数的倾向，且适合在计算机上运算，计算精度很高。
    对本文算法的一个最大质疑可能是：随着统计方法的改进，有可能直接获得城乡混合的收入调查数据，这似乎会使本文算法失去意义。但城乡混合的收入调查需要使用分层抽样技术，这一技术容易导致较大的抽样误差，而且，直接使用城乡混合的收入调查数据计算混合基尼系数，将无法进行分解分析。
    本文分解方法有待深化的方面在于：只提供了涉及两个分组的分解形式，若将其推广到多个分组，结果可能非常复杂，这需要进一步研究。
    参考文献：
    [1]陈希孺，2004：《基尼系数及其估计》，《统计研究》第8期.
    [2]陈宗胜，2000：《中国居民收入分配差别的深入研究》，《经济研究》第7期.
    [3]陈宗胜，2002：《关于总体基尼系数估算方法的一个建议》，《经济研究》第5期.
    [4]陈宗胜、周云波，2002：《再论改革与发展中的收入分配》，经济科学出版社.
    [5]程永宏、糜仲春，1998：《利用个人收入分配函数确定基尼系数的新方法》，《华东经济管理》第1期.
    [6]董静、李子奈，2004：《修正城乡加权法及其应用》，《数量经济技术经济研究》第5期.
    [7]胡祖光，2004：《基尼系数理论最佳值及其简易计算公式研究》，《经济研究》第9期.
    [8]李强、洪大用等，1995：《我国社会各阶层收入差距分析》，《科技导报》11期.
    [9]李实，2003：《中国个人收入分配研究回顾与展望》，《经济学季刊》第2卷第2期.
    [10]李实，2000：《对收入分配研究中几个问题的进一步说明》，《经济研究》第7期.
    [11]李实，2002：《对基尼系数估算与分解的进一步说明》，《经济研究》第5期.
    [12]李实、赵人伟，1999：《中国居民收入分配再研究》，《经济研究》第4期.
    [13]李实、赵人伟等，1998：《中国经济转型与收入分配变动》，《经济研究》第4期.
    [14]厉以宁、秦宛顺，1997：《现代西方经济学概论》，北京：北京大学出版社.
    [15]罗默，1999：《高级宏观经济学》，中译本，北京：商务印书馆.
    [16]万广华，2005：《收入差距的地区分解》，《世界经济文汇》第3期.
    [17]万广华，2004：《收入分配的度量与分解：一个对于研究方法的评介》，《世界经济文汇》第1期.
    [18]王祖祥，2001：《分组数据条件下基尼系数的有效估算方法》，《数量经济技术经济研究》第8期.
    [19]魏后凯，1996：《中国地区间居民收入差异及其分解》，《经济研究》第11期.
    [20]徐宽，2003：《基尼系数的研究文献在过去八十年是如何拓展的》，《经济学季刊》第2卷第4期.
    [21]赵人伟，李实等，1999：《中国居民收入分配再研究》，中国财政经济出版社.
    [22]Cowell,A., 2000, Measurement of Inequality, in Handbook of Income Distribution, eds by A. Atkinson and F. Bour guignon, North Holland.
    [23]Brown, J. A. C. and Mazzarino, G., 1984, "Drawing the Lorenz Curve and Calculating the Gini Concentration In dex from Grouped Data by Computer." Oxford Bulletin of Economics and Statistics. Oxford: Aug 1984. Vol. 46, Iss. 3: pg. 273.
    [24]Dollar, D. and Kraay, A., 2001, Growth is Good for the Poor, Mimeo, World Bank, Washington D. C., PolicyResearch Working Paper, 2587, 11-19.
    [25]Dorfman, Robert, 1979, "A Formula for the Gini Coefficient", Review of Economics and Statistics, 61, 146-149.
    [26]Johnson, G., 2002, 《1978以来，中国的城乡收入差距拉大了吗？》，《经济学季刊》第1卷第3期.
    [27]Kendall, Maurice G., and Alan Stuart , 1977, the Advanced Theory of Statistics, Vol. 1, Distribution Theory, 4thed. London: Charles Griffin.
    [28]Lambert, Peter J., 1989, the Distribution and Redistribution of Income: A Mathematical Analysis, Cambridge, Massachusetts: Basil Blackwell Inc.
    [29]Lambert, Peter J. and J. Richard Aronson, 1993, "Inequality Decomposition Analysis and the Gini Coefficient Revis ited", The Economic Journal, 103, 1221-1227.
    [30]Lee, J, 2000, "Changes in the source of China's Regional Inequality", China Economic Review, 11 (3): pg232- 45.
    [31]Ogwang, Tomson, 2000, "A Convenient Method of Computing the Gini Index and its Standard Error." Oxford Bul letin of Economics and Statistics. Oxford: Feb 2000. Vol 62, Iss. 1,; pg. 123.
    [32]Sundrum, R. M, 1990, Income Distribution in Less Developed Countries, Routledge, Londen and New York.
    [33]Silber, Jacques, 1989, "Factor Components, Population Subgroups and the Computation of the Gini Index of Inequal ity". The Review of Economics and Statistics, Vol. 71, No. 1(Feb., 1989), pg101-115.
    [34]Yao, shujie, 1999, "On the Decomposition of Gini Coefficients by Population Class and Income Source: a SpreadsheetApproach and Application," Applied Economics, 1999, 31, 1249-1264.
    [35]Yizhaki, Shlomo, 1982, "Stochastic Dominance, Mean Variance and Gini's Mean Difference", American EconomicReview, 1982, 72, 178-185.