技术进步偏向、资本效率与劳动收入份额变化(一)

内容提要：本文构建了一个劳动收入份额相对于资本收入份额变化的新古典经济学理论分析框架，并使用中国1990～2010年的数据进行了实证计量分析。分析结果表明，中国劳动与资本之间的要素替代弹性显著大于0，且显著小于1，并且生产过程中的技术进步是偏向于劳动增强型的，表现为劳动效率持续快速提高，而资本效率则持续下滑，正是偏向劳动增强型技术进步的速率高于资本深化的速率直接导致了劳动收入份额相对于资本收入份额的持续下降。进一步的深入分析则表明，导致资本效率下滑引起劳动收入份额也持续下降的深层次原因则主要是中国企业没能随着市场环境的变化而拓展升级其生产价值链，以致没能实现生产经营方式的转型升级。而政府经济政策偏差形成的银行业高利差导致的扭曲性收入转移、城市房地产价格的持续飙升导致的实体经济企业房地租成本上升，以及政府税收的持续快速增长对实体经济企业收益的挤压，则更进一步加剧了这一趋势。

关键词：CES生产函数，要素替代弹性，偏向性技术进步，资本效率，劳动收入份额

一、引言

根据中国国家统计局每年发布的国民经济核算数据计算可以看出，近二十多年来，在中国每年的国内生产总值中，劳动收入所占的份额基本上呈现下降的趋势，特别是1995年以后则是持续下降。根据全国各省份收入法国内生产总值核算数据汇总计算，中国劳动收入在GDP中所占的份额，1995年为51.44%，随后则持续下降，到2007年已下降到了39.74%，2008年以后受世界金融危机和民工荒的影响，中国企业盈利水平下降，使得企业盈利占比有所下降，从而使劳动收入占比又有所回升，但2010年中国劳动收入份额占GDP的比例也只有45.01%，仍然大幅低于20世纪90年代的水平。

劳动收入占GDP比重持续下降的状况近年来已引起了中国经济学界和政府的高度关注，对于劳动收入份额下降的原因，已是众说纷纭。归纳来看，文献中给出的原因主要有：(1)资本的强势与资本谈判地位的强化导致利润对工资的侵蚀^[1～3]；(2)产业结构的转型与变化^[4，5]；(3)节约劳动技术的开发与应用导致的劳动节约型技术进步^[6，7]；(4)劳动收入份额随着经济发展的U形变化规律^[8]。上述这些研究尽管分析的视角各自不同，得出的结论也不一致，甚至相互矛盾，但却都使用了SNA核算的数据，并都或多或少地依据了新古典经济学的理论。对这种分析方法，冯志轩(2012)提出了批判，认为基于SNA核算体系的劳动报酬占比这一指标本身不具有直接的理论意义，新古典经济学在解释劳动报酬占比时存在问题和缺陷，并基于投入产出表数据用马克思主义经济学重新测算了中国劳动报酬占比指标及其近年来的变动趋势，认为近年来中国劳动收入占比的剧烈下降与国际整体环境相关^[9]。

然而，不论是基于SNA核算数据使用新古典经济学理论的测算分析，还是基于投入产出表数据(其实投入产出表本身就是SNA核算体系的一个组成部分)使用马克思主义经济学理论的测算分析，所得结果都是近年来中国劳动报酬份额持续下降，二者并无本质差别，这表明新古典经济学和马克思主义经济学都可以用来分析劳动报酬份额的变化。但是，这并不是说中国经济学界在使用新古典经济学理论分析中国劳动报酬份额变化问题上就不存在问题，纵观这方面的已有研究，主要的问题是研究分析中没有严格一致的新古典经济学理论模型框架。实际上，在已有的研究中，有些分析结论只是主观判断的结果，而有些分析结论虽然是通过计量经济模型实证分析得出的，但所构建的计量经济模型缺乏理论严格一致的经济学理论模型基础，甚至理论模型的构建中本身就存在矛盾，以致解释变量的选择有很大的随意性且只停留在表层，导致分析的结论缺乏深度，甚至不正确。实际上，资本的强势、产业结构的变化以及劳动节约型技术进步，并不是近十几年来才出现的现象，这些现象可以说在20世纪90年代以前就都已经存在，那么为何以前没有导致劳动报酬份额的下降，而到了90年代中期以后却导致了劳动报酬份额的下降呢？显然，这是已有研究不能回答的问题。至于说劳动收入份额与经济发展U形相关的规律，即使真的存在，也只不过是统计数据所显示的浅层表面现象，并没有揭示出劳动收入份额变化背后的原因及其作用机制。因此，对此问题，有必要进一步深入的研究。

本文将根据中国经济体制的特征，使用经济学理论构建出一个理论严格一致的经济学数理模型框架，以揭示经济发展过程中决定劳动收入份额变化的因素及其作用机制，并据此来构建计量经济模型进行实证分析，对近十多年来中国劳动收入份额下降的直接原因和深层原因进行分析。

二、经济理论框架

假设企业生产经营的目标是利润最大化。在文献中，通常直接使用微观经济学的厂商理论，将企业利润最大化的一阶条件表述为：要素的报酬率等于要素的边际产出。这里，排除了政府的存在。虽然不考虑政府的存在会简化分析，但是由于任何国家都不是无政府的，企业的产出不可能只在资本和劳动二者之间进行分配，所以不考虑政府的存在或许在抽象的理论分析中可行，而在具体的核算分析中将会引起较大的偏差。因此，为了实际核算的需要，必须给出政府税收存在条件下的企业利润最大化的一阶条件。记企业的产出为Y_t，生产过程中的资本投入和劳动投入分别为K_t和L_t，资本的技术水平为A_t，劳动的技术水平为B_t，生产函数为Y_t=F(A_tK_t，B_tL_t)，资本的租金率为r_t，折旧率为δ_t，劳动的工资率为w_t，生产过程中政府所征收的生产税税率为τ_t，则企业的利润可以写为：

π_t=F(A_tK_t，B_tL_t)-r_tK_t-δ_tK_t-w_tL_t-τ_tF(A_tK_t，B_tL_t) (1)

将利润函数式(1)对资本K_t和劳动力L_t分别求导，可得企业利润最大化的一阶条件为：

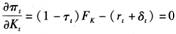(2)

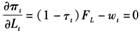(3)

这表明，资本和劳动的报酬率分别为用生产税税率扣减后各自的边际产出。假设生产过程规模报酬不变，则由一次齐次性生产函数的欧拉定理可得：

Y_t=K_tFK+L_tFL (4)

将式(2)和式(3)均代入式(4)，则可得出具有政府生产税税收参与分配的社会产出初次分配公式为：

Y_t=(r_t+δ_t)K_t+w_tL_t+τ_tY_t (5)

式(5)中，等式右边第一项为资本所得，由资本租金收入和折旧构成，第二项为劳动所得，由劳动报酬构成，第三项为政府所得，由生产税税收构成。

为了进一步深入地进行理论分析，需要给定生产函数的具体形式，研究普遍都采用柯布—道格拉斯(Cobb-Douglas，1928)生产函数形式，但是C-D生产函数隐含着劳动与资本的替代弹性为1的假设，而此假设已被国外众多的实证研究证明不符合经济现实。如奇瑞科等(Robert S. Chirinko et al.，2011)根据1860个企业的面板数据估计得出要素替代弹性为0.40^[10]，科卢珀等(Rainer Klump et al,，2007，2008)使用美国数据估计得出的要素替代弹性为0.6^[11]，使用欧洲地区的数据估计得出的要素替代弹性为0.70^[12]，斯密(Smith，2008)使用英国的面板数据估计得出的要素替代弹性为0.40^[13]。大多数的研究表明，劳动与资本的替代弹性值在0.40～0.60(Chirinko，2008)^[14]。近些年来国外的经济研究文献中生产函数已大多使用CES函数形式。因此，考虑到使理论分析的结果更具有一般性和更广泛的适用性，可以设定生产函数为CES形式，即有：

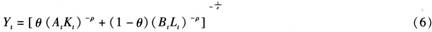
式(6)中，θ∈(0，1)是反映生产过程中两种要素的重要性的分配参数，ρ=(1-σ)/σ≥-1是反映两种生产要素相互可替代性的替代参数，σ∈(0，∞)则为替代弹性。如果替代弹性σ=∞，则两种生产要素具有完全的替代性，此生产函数就退化为线性生产函数；如果替代弹性σ=1，则此生产函数就退化为柯布—道格拉斯生产函数；如果替代弹性σ=0，则两种生产要素相互不可替代，则此生产函数就退化为列昂梯夫固定比例生产函数。因此，此CES生产函数涵盖了常用的几种生产函数，具有更普遍的适用性。具有CES生产函数的经济系统，在向其稳态均衡路径运行的过程中，劳动增强型技术和资本增强型技术都将变化，要素收入份额也将变化^[15]。

由式(6)给出的生产函数，可以推导出资本和劳动的边际产出分别为：

将资本的边际产出式(7)代入式(2)，并将劳动的边际产出式(8)代入式(3)，则得到资本报酬率和劳动报酬率的表达式分别为：

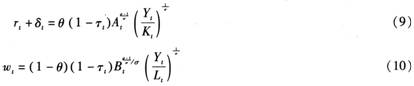
由式(9)和式(10)，容易推导出在社会最终产品中资本的收入份额和劳动的收入份额分别为：

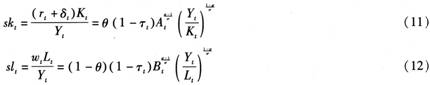
由式(11)和式(12)可以看出，资本收入份额的变化取决于产出资本比即资本产出率的变化和资本增强型技术进步的速率，而劳动收入份额的变化则取决于劳动生产率的变化和劳动增强型技术进步的速率，并且二者都随着政府生产税税率的上升而下降。

为了消除政府生产税税率变化的影响，专注考察两种生产要素收入相对份额的变化，用式(12)除以式(11)，可得劳动与资本收入相对份额为：

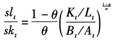(13)

在式(13)中，K_t/L_t为单位劳动的平均资本，其值的增大称为资本深化，其值的减小称为资本浅化，由于资本可以积累，而劳动不可以积累，所以在经济发展的过程中通常是资本不断地持续深化。由式(13)可以看出，劳动与资本收入相对份额的变化取决于资本深化的速率和劳动增强型技术进步速率相对于资本增强型技术进步速率的大小，而相互关系的方向则取决于要素替代弹性的大小。如果要素替代弹性σ＞1，则劳动与资本收入相对份额随着资本深化而下降，并随着劳动增强型技术进步速率相对于资本增强型技术进步速率的上升而上升；如果替代弹性σ＜1，则劳动与资本收入相对份额随着资本深化而上升，并随着劳动增强型技术进步速率相对于资本增强型技术进步速率的上升而下降；如果替代弹性σ=1，则劳动收入份额和资本收入份额均为常数，既不随着资本深化或浅化而变化，也不随着有偏或无偏(中性)技术进步速率的变化而变化。

因此，要分析劳动与资本收入相对份额的变化，就需要计算资本深化的速度及劳动增强型和资本增强型两类技术进步各自的速率，并且还需要计算出资本和劳动两类生产要素的替代弹性。显然，资本深化的速度可以根据现有的统计数据直接计算，而劳动增强型和资本增强型两类技术进步的速率，以及要素替代弹性则需要使用计量经济模型进行估计。为了能够估计出劳动增强型和资本增强型两类技术进步的速率，假设二者各自的变化速率为常数，即有A_t=A₀e^at，B_t=B₀e^βt，分别代入式(9)和式(10)，然后取对数则得到：

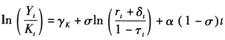(14)

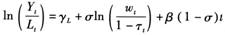(15)

式中，γ_K、γ_L均为常数。式(14)和式(15)可组成一个联立方程组，使用统计数据对此方程组进行估计，就可得到要素替代弹性σ以及资本增强型技术进步速率α和劳动增强型技术进步速率β的估计。

三、数据与计量分析

生产函数中的产出是企业的最终产出，其总量就是国内生产总值GDP，生产过程中劳动力投入可以用实际就业的劳动力人数度量，资本投入可以用资本存量来度量。

在中国，国家统计局每年的《中国统计年鉴》中都公布有按当年价格计算的名义GDP数值和按可比价格计算的环比与定基GDP指数。用各年的当年价格名义GDP与基期的名义GDP相比就可以计算出名义GDP指数，该指数包含有社会最终产出的实际增长和价格变动两种成分。然后，用名义GDP指数去除可比价格GDP指数就可得到GDP缩减指数。有了GDP缩减指数，用它去除各年的名义GDP就可得到各年的实际GDP数值。本文的GDP缩减指数以2000年为基准，所计算的实际GDP是2000年价格GDP数据。

对于劳动力投入，每年的《中国统计年鉴》都公布有各年年末的全社会就业人员总数，将相邻两年年末就业人员数简单平均就得到了各年的平均就业人数，可看作是各年劳动力投入数量序列。

（未完待续）

责任编辑：夏雨