高维模型选择方法综述（二）

1.1.2两步法LASSO方法
    为了提高LASSO方法参数估计的准确性和相合性，对其进行修正是必要的，为此我们介绍两步法LASSO的两个例子：Relaxed LASSO与Adaptive LASSO。
    Relaxed LASSO是由Meinshausen[17]提出的。它的主要思想为：先计算LASSO在由全路径方法选取的调整参数下的参数估计结果（调整参数选择将在第五节讨论），选出合适的变量；对于选出的变量，再次应用LASSO，但减小或者消除惩罚因子的作用，因此第二步不进行变量选择。由此，Relaxed LASSO会得到与普通LASSO方法同样的模型，但是回归参数估计不同，前者不会过度缩小非零参数，因为模型选择和参数估计被分成两个独立的过程。
    上述方法是基于第一步LASSO能够选出真实模型的前提假设的。放松惩罚项可以更准确的估计参数值。若令第二步的惩罚项为零，则为典型的LASSO/OLS方法。一些经验和理论的结果表明，该方法优于普通的LASSO方法。更多的可参考Meinshausen[17]。
    另一个两步法LASSO的例子是Zou[18]提出的Adaptive LASSO。该方法利用全模型最小二乘估计计算不同变量的惩罚项。若某变量最小二乘参数估计值较大，则其更可能为真实模型中的变量，因此该变量在惩罚最小二乘估计时惩罚项应较小，以确保其有更大的概率被选入模型。Adaptive LASSO方法的惩罚项为
    
    其中λ，θ＞0为调整参数。注意到权重都是根据数据确定的，所以称为Adaptive LASSO。
    同Relaxed LASSO性质类似，Adaptive LASSO也可以减弱LASSO对非零系数的缩减，从而减小偏差。但Adaptive LASSO更重要的意义在于当变量个数固定而样本量趋于无穷时，其具有相合性，且这些参数估计的分布与事先给定非零变量位置的最小二乘得到的参数估计的分布渐近相同。
    1.1.3有序变量的模型选择方法
    有时数据变量呈现有序的结构，例如根据密度排列的蛋白质的光谱波长等。在这种情况下，我们希望相邻变量之间的系数估计相差不要太大，即选择模型中的变量总是与相邻变量同时出现。LASSO方法并不能实现这个目的。Tibshirani等（2005）[19]提出了Fused LASSO以达到上述目的。该方法在LASSO惩罚项基础上添加了相邻系数之差的惩罚项，即最小化下述式子
    
    其中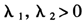为调整参数。第二项惩罚项是对相邻变量系数差距的惩罚，可鼓励参数局部平缓变化。Fused LASSO一般用于变量存在自然顺序的模型选择中，它给出的参数估计在局部近似于常数。给定调整参数的值，则可利用二次算法来求解上述最小化问题。
    1.1.4未知分组的群组模型选择方法
    当一组强相关的解释变量同时存在时，普通的LASSO方法倾向于选取其中一个变量。但有的情形下，我们希望将这一组强相关的变量都选出来。事实上，前面提到的Bridge方法的惩罚项是严格凸的，并且具有群组效应，但是不能实现模型选择。Zou和Hastie[20]结合LASSO方法与Bridge方法的优点，提出了既有群组效应又能进行模型选择的Elastic Net（EN）方法来解决未知变量分组情况下的组群模型选择。该方法的简单形式如下：
    
    上述参数估计可视为LASSO估计（参数为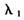）与岭回归估计（参数为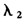）的结合，经历了两次系数缩减的过程。这个操作不能够明显降低参数估计的方差，但却带来了额外的偏差。最简单的调整方法就是将上述参数估计结果乘以（1+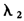）进行尺度调整，Zou和Hastie[20]的模拟研究表明这样调整的预测效果较好。在参数数目随样本量增加的情形下，Zou和Zhang[21]将EN方法进行了推广。
    EN方法在微阵列数据分析中有重要应用，因为它倾向于把相关的基因作为一个组群同时删除或选择出来。除此之外，当变量有共线性性时，EN方法得到的选择模型的预测准确性比LASSO高，并且前者可以更好地处理变量数目超过样本量的问题。具体可以参见Zou和Hastie[20]的文章。
    1.1.5已知分组的群组模型选择方法
    与上一小节不同，有些情形下我们可以知道变量的分组情况，在进行模型选择时，我们希望能同时保留或删除同一组的变量。Yuan和Lin[22]提出的Group LASSO，Zhao等[23]提出的Composite Absolute Penalty（CAP）方法都是处理上述问题的方案。
    
    上述通过调整惩罚项以实现特定模型选择目的的思想可以推广到更多的方法。例如已知重要的变量可以不加惩罚因子，而疑似噪声的变量可以配置更大的惩罚项。对不同的变量给予不同的惩罚项可以加入选择的先验信息，这样惩罚最小二乘估计就会变得更加灵活。
    1.2SCAD方法
    Smoothly Clipped Absolute Deviation（SCAD）方法是由Fan和Li[24]提出的，其惩罚项定义为
    
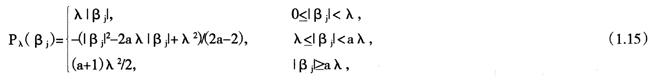
    其中a，λ＞0为调整参数。Fan和Li（2001）[24]的文章中建议参数取值a=3.7。当设计阵列正交时，利用SCAD方法得到的参数估计显示表达如下：
    
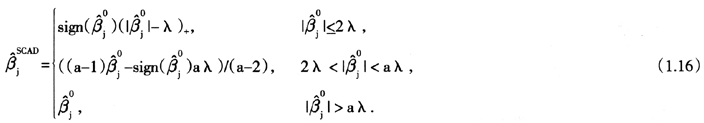
    SCAD方法有两方面的优势：一是其计算成本较低，二是参数估计对数据有连续性，因而较为稳定。较之岭回归方法，SCAD方法减少了选择模型预测方差。较之LASSO方法，SCAD方法减小了对参数估计的偏差，即过度缩减系数的现象。
    1.3Oracle性质
    Fan和Li[24]出了模型选择方法应当满足的三条性质，又被称为Oracle性质：
    1）稀疏性：模型选择方法的参数估计应自动实现系数的稀疏性，即将一些不重要的变量系数变为零。
    2）无偏性：参数估计应无偏或近似无偏，至少对于系数较大的变量的参数估计应如此。
    3）连续性：参数估计应对于数据是连续的，以避免模型预测的不稳定性。同时满足上述三条的模型选择方法称为满足Oracle性质的方法。
    为了进一步阐述该性质，假设设计阵是列正交的，惩罚最小二乘的一般表达式可改写为：
    
    但与此同时，Leeb和Potscher[25]指出Oracle性质只是基于逐点形式的误差和估计，不具有一致评估整个模型的功效，而对模型的一致评估才是对参数做统计推断和评估方法好坏的基本出发点。Leeb和Potscher[25]的文章详细阐述了Oracle性质定义的纰漏，并建议不将此作为评判模型选择方法好坏的标准。他们指出Oracle性质与Hodges估计有相似的问题，即只在逐点意义下满足一些好的渐近性质，但在有限样本的情形下这些性质又明显不成立。例如，Leeb和Potscher[25]证明了任何利用上述疏系数方法得到的所谓的相合参数估计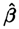，其如下调整刻度的均方误差在样本量增加的时候发散到无穷：
    
    另外，Leeb和Potscher[26]以及Leeb和Potscher[27]还得出了一些容易被忽视的结论，即以数据为导向的模型选择方法对后续参数估计有很大影响，即使对所谓的满足相合性的模型选择方法选取的模型进行参数估计，也不能等同于对真实模型进行参数估计。在求参数估计的分布时只能推导有限样本的密度估计，不能以渐近分布代替。有兴趣的读者可参考Leeb和Potscher[26]及Leeb和Potscher[27]。

（未完待续）