“单独”育龄妇女总量、结构及变动趋势研究

    内容提要：文章以“单独”育龄妇女为研究对象，通过建立随机微观人口仿真模型，研究“单独”育龄妇女总量、结构和变动趋势，结果表明，如果现行生育政策不变，“单独”育龄妇女总量在未来三四十年内持续增长的趋势不可逆转，且增长速度很快，年均增长速度在10‰以上，2050年“单独”育龄妇女占育龄妇女的比例将达到50％以上，总量超过1.2亿。如果放开“单独”二孩政策，2050年“单独”育龄妇女占育龄妇女的比例将在50％以下，总量仍超过1亿。如果全面放开二孩政策，2050年“单独”育龄妇女占育龄妇女的比例将在30％以上，总量在1亿以内。
    关键词： 单独/家庭/随机人口/微观仿真
    作者简介：王广州，中国社会科学院人口与劳动经济研究所，研究员。   
    中国计划生育政策、特别是30多年来独生子女政策的全面推行，不但改变了中国人口发展的历史趋势，改变了中国家庭、社会的基本结构，而且出现了上亿的独生子女，形成了具有鲜明特点的独生子女家庭类型。目前对独生子女面临问题的研究较多(风笑天，2008；肖富群、风笑天，2010)，这些研究不仅涉及独生子女总量、结构估计(宋健，2005)，也涉及独生子女的教育、健康等(郭翠菊，2000；方拴锋等，2010)，同时还涉及独生子女父母的养老和独生子女的死亡与伤残等(周长洪，2009；姜全保、郭震威，2008)。
    以往研究通常以独生子女个人作为研究对象，其优点是忽略了家庭关系，简化了研究对象和研究内容，缺点是没有家庭成员的信息，不清楚夫妇或其他家庭成员的独生属性。把家庭关系纳入研究，如考察独生子女的家庭状况和生育行为，无疑增加了额外的信息来源，但同时也增加了研究的工作量和难度。本文试图从“单独”育龄妇女①出发，定量分析不同生育政策条件下，“单独”育龄妇女总量、结构和变动趋势。
    一、研究方法与数据来源
    (一)概念界定
    研究全部人口的“单独”家庭总量，首先是数据获得十分困难。由于中国现有的大型调查数据中只有2005年全国1％人口抽样调查数据提供了30岁及以下人口有无兄弟姐妹的信息，因此30岁以上人口或夫妇的独生属性并不清楚。尽管30岁以上人口在出生时或年龄较小时独生子女总量和比例都远低于目前的低龄人口，但由于死亡的影响会造成当前无兄弟姐妹的人口比例上升。其次是是否为独生子女涉及两代人，是否为“单独”又涉及婚姻和家庭关系，这给定量研究造成一些困难。鉴于此，为了简化和明确人群的范围界定，本文以育龄妇女为观察对象确定“单独”家庭，这样便于对育龄妇女本人、丈夫及子女的独生属性进行认定，但会漏掉丧偶且没有再婚家庭中丈夫为独生子的“单独”家庭。由于育龄人群的死亡概率相对较低，所以遗漏的“单独”育龄妇女家庭规模不大。
    (二)研究方法的确立
    对“单独”育龄妇女总量、结构和变动趋势的估计涉及已婚育龄妇女本人及其丈夫是否为独生子女两个基本条件。从研究方法来看，在现有的宏观模型中，无论是一般的人口预测模型还是递进人口预测模型，虽然可以用来研究独生子女的总量结构，但涉及婚姻和家庭，特别是判断配偶的独生属性却很难实现。为了解决宏观模型需要较多参数和模型过于复杂的问题，本研究采用随机微观人口仿真模型。建模的思路和方法主要是通过计算机模拟个人的独生属性和家庭的动态变化过程，在模型参数估计过程中采用随机人口预测模型的参数估计和建模方法，因此，计算机随机微观人口仿真模型是把随机人口预测模型和微观人口仿真模型的优点结合起来，可以实现动态模拟“单独”育龄妇女家庭总量和变动趋势等多种属性的统计分析。虽然随机微观人口仿真模型建模非常复杂，但其突出的优点是可以通过非常小的概率样本研究全国人口的仿真问题②。
    (三)方法的检验
    为了检验随机微观人口仿真模型的有效性、克服微观仿真模型因运算量巨大而耗费时间的问题，本研究采取尽可能小的样本量来进行随机微观人口仿真，并把模型运算结果与宏观人口模型或实际调查数据进行比较来检验模型的可靠性。此外，采用较小的样本也有利于控制误差大小和甄别误差来源。本研究在建立和验证模型的过程中，以1990年全国第四次人口普查1％抽样原始数据为基础进行再抽样，抽取32469人概率样本，抽样比为全国人口的2.87／10万，以此数据为基础进行随机微观人口仿真模型检验，宏观模型采用1990年全国第四次人口普查100％汇总数据为运算基础数据。
    由于随机人口预测模型具有不确定性，需要确定是随机因素的误差还是模型本身的错误。实践经验表明，为了确定误差的来源与大小，参数越简单也就越容易发现问题和进行模型的一致性检验。由于人口变动的主要方面是出生、死亡和迁移，在不考虑迁移的情况下，出生、死亡参数决定人口的未来。考虑到模型检验的便捷性，本文在模型检验过程中仅对生育水平和平均预期寿命进行参数假定，从而对随机微观人口仿真模型和随机宏观人口预测模型的差异进行分析和比较。表1给出了1990～2010年模型检验的基本参数假定，其中1995、2000、2005年中间年份的参数是根据1990和2010年参数线性插值得到，并没有对相应年份参数的具体大小进行分析，主要目的是看总量等宏观数据的模型运算结果与2010年的普查数据是否可以吻合。
     
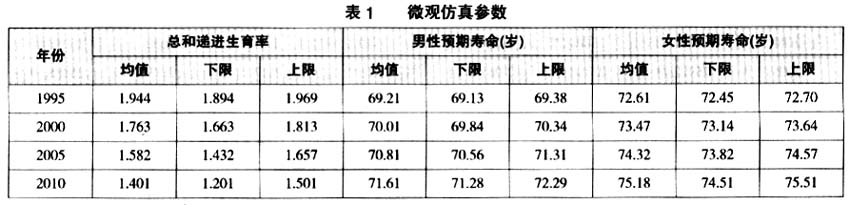
    从出生人口规模的比较来看(见表2)，2010年小样本随机微观人口仿真(以下简称小样本仿真)模型样本加权后的出生人口数均值与随机宏观人口模型预测均值的误差在±7％以内，下限的误差在±10％以内，上限的误差在±15％以内。与人口抽样调查和人口普查数据相比，小样本仿真样本加权后的出生人口数均值均明显偏大，这主要是由于总和递进生育率与调查相比偏大。例如，2000年全国人口普查的总和生育率为1.22，总和递进生育率为1.3881(王广州，2005)，而本文2000年随机微观人口仿真模型的总和递进生育率均值为1.763，下限为1.663，上限为1.813，因此，人口仿真模型的出生人口数一定比人口普查所对应的出生人口数大很多。
    从已婚有配偶育龄妇女的总量来看(见表3)，1995年以来小样本仿真样本加权后的已婚有配偶育龄妇女数均值与调查值的误差在±4％以内，下限的误差在±6％以内，上限的误差在±3％以内。误差较小的是1995年和2000年，小样本仿真样本加权后的已婚有配偶育龄妇女数的均值与调查值的误差在±2‰以内，2010年误差在3％以内。误差最大的是2005年，已婚有配偶育龄妇女数的均值的相对误差为3.58％，估计值下限的误差为5.17％，上限与调查值的误差为2.57％。
    从总人口的情况来看(见表4)，由于误差相抵和样本量的原因，总人口的误差与出生人口等明显不同。从表4可以看到，2010年小样本仿真样本加权后总人口数的均值与随机宏观模型预测均值的误差在±7‰以内，下限的误差在±6‰以内，上限的误差在±12‰以内，可见总人口的误差比出生人口误差低一个数量级，这既符合抽样理论，也符合人口预测的基本原理。同样，与直接调查数据相比，总人口的小样本仿真预测值均值的误差也很小，除了2005年外，与普查和调查推断总人口的误差在5‰以内，而且总人口的调查值在随机微观人口仿真结果的上、下限之间。
     
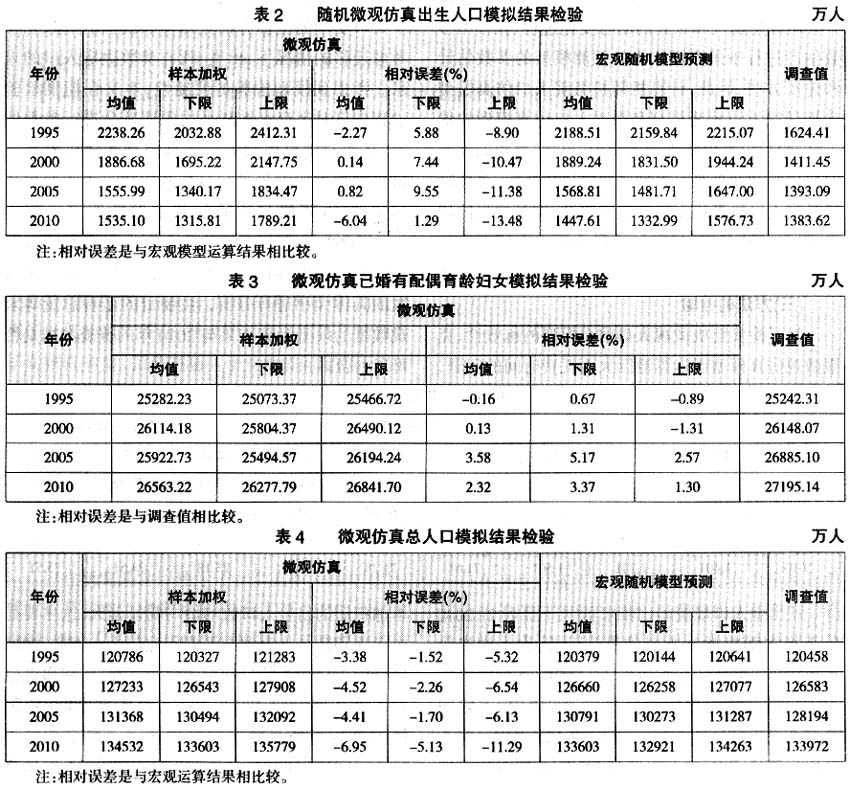
    总之，从以上的比较分析可以看到，即便是抽样仿真原始数据的样本量很小，但小样本仿真模型与随机宏观人口预测模型具有高度的一致性，这与齐险峰、郭震威(2007)用2000年人口普查抽样1‰原始数据(118万人)进行微观仿真和宏观模型运算结果进行检验所得出的结论一致。
    (四)主要数据来源
    在微观仿真过程中，样本量的增加可以减小随机误差，但随着样本量的扩大，随机微观人口仿真模型运算时间剧增，因此需要在随机误差大小和计算机运算时间之间把握一个平衡。本文仿真基础数据采用1990年人口普查原始数据的抽样数据，抽样方法采用按户抽样，共抽取65135人，相当于1990年全国总人口的5.76／10万。除了微观仿真原始抽样数据外，仿真模型基本参数采用1990年全国人口普查汇总数据和1％抽样原始数据推算。此外，本文还使用2005年全国1％人口抽样调查作为参数估计和独生子女总量、结构估计的基础数据，并据此进行模型分析和误差区间控制。
    二、“单独”育龄妇女总量估计
    通过对2005年全国1％人口抽样调查原始数据家庭户分析，可以估计2005年全国15～30岁“单独”育龄妇女的情况(见表5)。从表5可以看到，2005年全国15～30岁“单独”育龄妇女调查值为1229.55万人，与模型估计值的均值1597.88万人有较大差距。估计值与调查值之间存在较大差距的原因在于2005年1％人口抽样调查原始数据中户主不在本户的比例偏高。2005年全国1％人口抽样调查原始样本数据总户数为996589户，而其中有户主登记的有741230户，占74.38％，没有户主的比例为25.62％。在有户主的家庭中，男性户主占84.79％，女性户主占15.21％。在原始数据中，夫妻双全户为437399户，丈夫是户主的为406 125户，占92.85％，妻子是户主的为31274户，占7.15％。由于男性独生子女比例大于女性，因此，尽管在人口总数上加权后误差不大，但内部结构受人口流动属性和独生属性之间性别差异的影响而产生误差。调查估计30岁以下育龄妇女“单独”的人数占仿真模型估计值的76.94％，可以推测，如果未调查到的分布与已知分布相同的话，并且补上缺失登记的没有户主的25.62％家庭户，二者的误差会大大缩小。
     
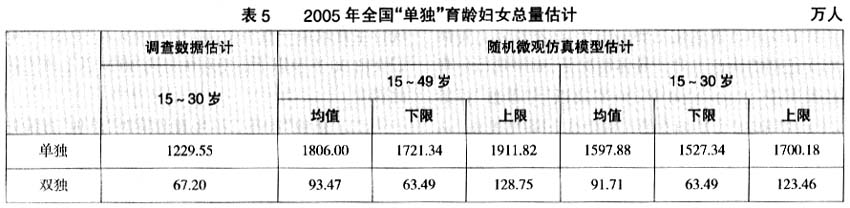
    根据以上误差分析和随机微观人口仿真模型运算结果，估计2005年全国“单独”育龄妇女总量在1800万人左右。其中，估计2005年全国“双独”育龄妇女总量在93万人左右。
    三、“单独”育龄妇女总量、结构及变动趋势
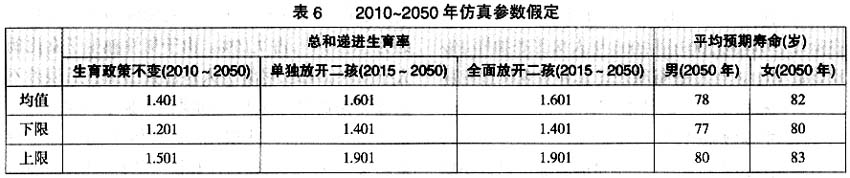
    生育水平的高低决定独生子女总量、结构及其变化趋势，独生子女总量、结构又进一步影响到“单独”育龄妇女的总量、结构和变动趋势。由于生育水平高低与生育政策密切相关，因此，未来生育政策走向将成为影响“单独”育龄妇女总量、结构的关键因素。未来生育政策可能包括继续实施现行生育政策、放开“单独”二孩和全面放开二孩。本研究根据这3种生育政策的选择和平均预期寿命的基本状况，并考虑到相关生育意愿调查结果，假定了2010～2050年总和递进生育率和平均预期寿命95％的区间估计(见表6)，并根据这些假定通过随机微观人口仿真，定量估计不同政策取向条件下未来“单独”育龄妇女总量、结构和变动趋势。
     
    (一)现行生育政策不变，“单独”育龄妇女总量将迅速增长，结构快速老化
    如果现行生育政策不变且生育水平保持基本稳定，中国总人口高峰将在2023～2025年出现，高峰时期总人口估计值的均值为13.92亿，上限为14.1亿左右，但超过的可能性很小。与此同时，育龄妇女总量在2012年左右达到高峰，高峰期育龄妇女总量在3.75亿左右，预计2050年育龄妇女总量将下降到2.20亿～2.36亿，届时育龄妇女总量比目前高峰期减少1.4亿～1.5亿左右。在此情况下“单独”育龄妇女总量将迅速增长、结构快速老化。
    首先，从“单独”育龄妇女总量变动趋势来看，全国“单独”育龄妇女预计在2045年左右达到高峰，高峰估计值的均值为1.22亿人左右，上限为1.28亿人左右。到2050年“单独”育龄妇女总量均值下降到1.20亿人左右，上限估计值下降到1.27亿人左右(见表7)。估计2050年“单独”育龄妇女总量是2010年的4.1～4.2倍，而到2050年预计育龄妇女总量将下降到2010年的62％～63％。可见，“单独”育龄妇女总量将增长迅速。而高峰后“单独”育龄妇女总量绝对人数下降的主要原因是长期低生育水平造成的育龄妇女总量的迅速减少。另外，从“单独”育龄妇女占育龄妇女比例的增长情况也可以看出“单独”化的变化。如果现行生育政策不变，估计2050年“单独”育龄妇女占育龄妇女的比例将由2010年的8％左右上升到2050年的53％左右。具体变化情况是，2016年之前“单独”育龄妇女比例每年增长不到1％，而2017～2046年，“单独”育龄妇女比例每年增长在1％以上。
     
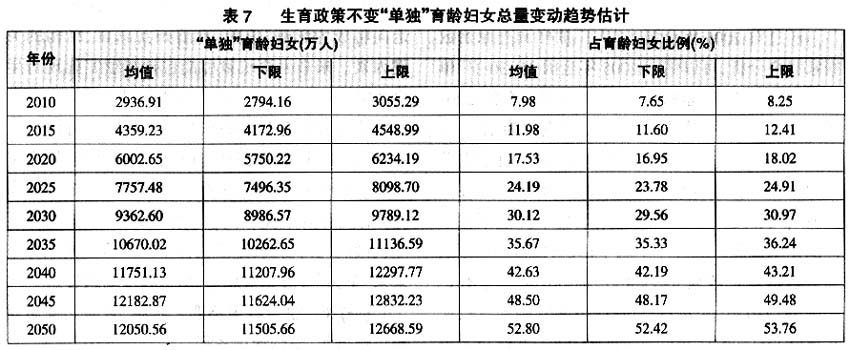
    其次，“单独”育龄妇女结构快速老化。“单独”育龄妇女的迅速老化主要是由于40岁及以上育龄妇女比例的快速上升。具体情况是，如果现行生育政策不变，2010～2050年，30岁及以下“单独”育龄妇女占“单独”育龄妇女的比例持续下降(见表8)。从不同年龄组“单独”育龄妇女绝对人数的变化情况来看，2010～2050年15～30岁“单独”育龄妇女增长了2倍左右，31～39岁“单独”育龄妇女增长了10倍左右，而40～49岁“单独”育龄妇女增长了40倍左右。如果现行生育政策一直不变，40年内将实现“单独”育龄妇女由30岁及以下占绝对优势向30岁以上占主体的转变。
    (二)“单独”放开二孩生育政策对“单独”育龄妇女总量、结构变化趋势影响不大
    如果2015年全国城乡统一放开“单独”二孩，而非“单独”育龄妇女生育政策不变。那么，总人口高峰将在2026～2029年左右出现，高峰总人口估计值的均值为14.01亿，上限为14.12亿左右。也就是说，2015年“单独”放开二孩政策所形成的高峰时期总人口超过14.2亿的可能性很小。与生育政策不变相比，2050年总人口估计值均值从生育政策不变的12.6亿上升到13.02亿，总人口估计值上限也由生育政策不变的12.80亿提高到13.18亿。同样，育龄妇女也将在2012年左右达到高峰，高峰期育龄妇女总量在3.75亿左右，到2050年育龄妇女规模持续下降到2.37亿～2.43亿，届时育龄妇女总量比高峰期减少1.3亿～1.4亿。“单独”育龄妇女总量、结构变化趋势总体上与生育政策不变相比变化不大，也就是说，“单独”放开二孩生育政策对“单独”育龄妇女总量、结构迅速变化趋势转变的影响不大。
     
     
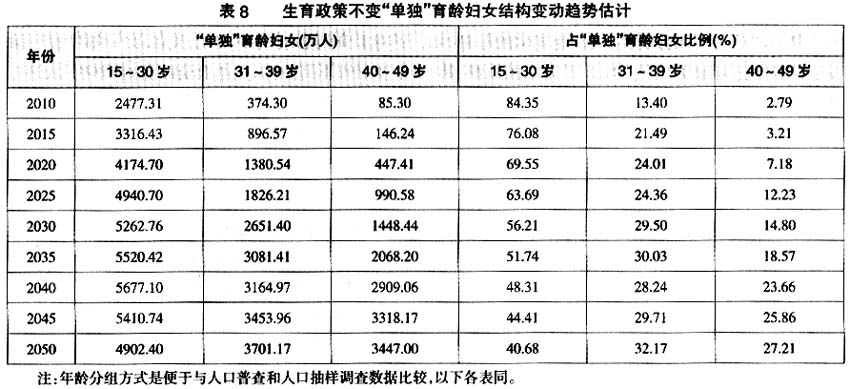
    第一，“单独”育龄妇女总量和比例迅速增加的趋势不变。即便是放开“单独”二孩政策，估计全国“单独”育龄妇女2050年仍将达到1.10亿～1.16亿人(见表9)，与生育政策不变相比“单独”育龄妇女大概减少不到1000万人。估计2050年“单独”育龄妇女总量是2010年的3.7～3.9倍。“单独”育龄妇女占育龄妇女的比例变化不大，估计2050年“单独”育龄妇女比例将达到46.49％，比现行生育政策不变“单独”育龄妇女的比例低7％左右。总之，单独”育龄妇女总量快速增长的总体状况与生育政策不变的情况相差不大。
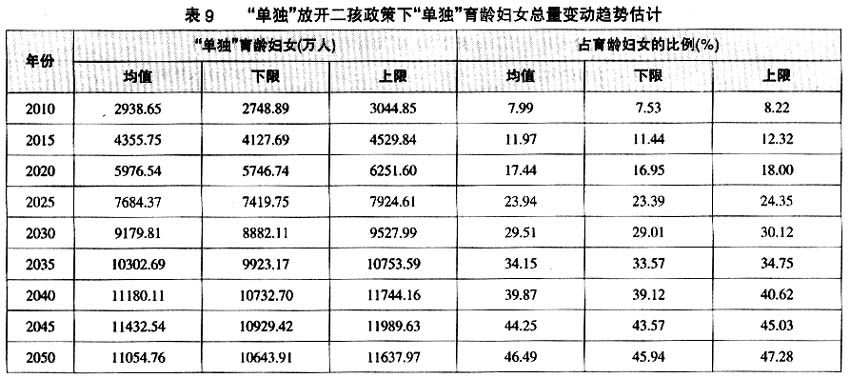
    第二，“单独”育龄妇女结构快速老化的趋势不变。如果2015年开始实施“单独”放开二孩政策，其他人群实行现行生育政策，预计2010～2050年，30岁及以下“单独”育龄妇女占“单独”育龄妇女的比例到2050年也将上升到38％左右，与现行计划生育政策不变相比下降不到3个百分点。同样，40岁及以上的“单独”育龄妇女占“单独”育龄妇女的比例将上升到2050年的30％以上，比计划生育政策不变上升不到3％。大体上全面实施“单独”放开二孩生育政策，到2050年30岁及以下、31～39岁和40岁及以上“单独”育龄妇女的比例将各占1／3左右(见表10)。可见，2050年之前“单独”育龄妇女快速老化的总体状况与现行生育政策不变的情况差别不大。
    (三)全部放开二孩生育政策，“单独”育龄妇女总量快速增长趋势缓解，内部结构老化加速
    如果2015年全国统一放开二孩，总人口高峰将在2029～2031年出现，高峰总人口估计值的均值为14.39亿，上限为14.59亿左右，即总人口超过14.6亿的可能性很小。与现行生育政策不变相比，2050年总人口估计值的均值从生育政策不变的12.6亿上升到13.87亿，总人口估计值的上限也由生育政策不变的12.80亿提高到14.42亿。同样，育龄妇女2012年达到高峰，高峰期育龄妇女总量在3.75亿左右，此后到2050年育龄妇女规模持续下降到2.59亿～2.70亿，育龄妇女总量比高峰期减少1.0亿～1.1亿左右。在此条件下，“单独”育龄妇女总量快速增长趋势缓解，内部结构老化加速。
    首先，“单独”育龄妇女总量快速增长趋势缓解。从“单独”育龄妇女总量的变动趋势来看，“单独”育龄妇女2040年左右达到高峰期的9200万人至1.0亿人，比现行生育政策不变的高峰时期“单独”育龄妇女人数减少3000万人左右。到2050年“单独”育龄妇女在8100万～9300万人之间，比现行生育政策不变减少3300万～3900万人。也就是说，如果全部放开二孩生育政策，2010～2050年“单独”育龄妇女总量增长情形将由现行生育政策不变的4.1倍左右减少到2.8倍左右。另外，从“单独”育龄妇女占育龄妇女的比例看，预计2050年“单独”育龄妇女比例将达到29.45％～34.33％，比现行生育政策不变情况低20％左右。
     
     
     
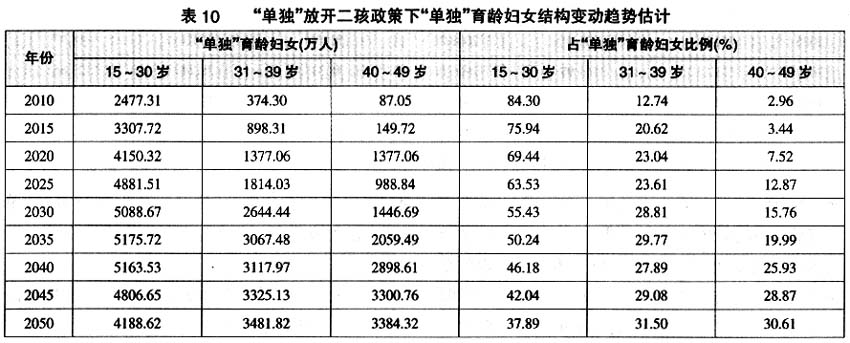
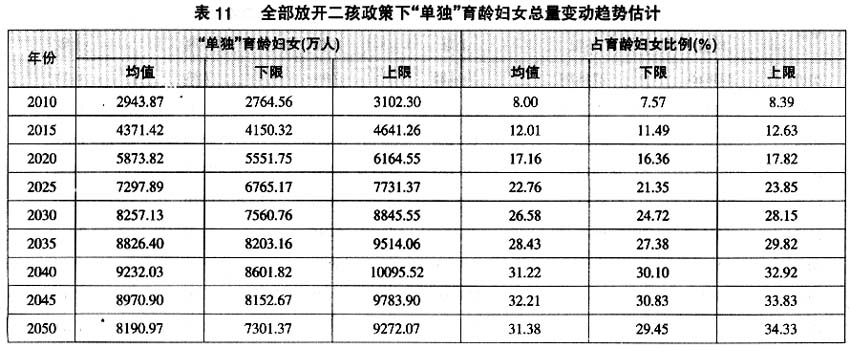
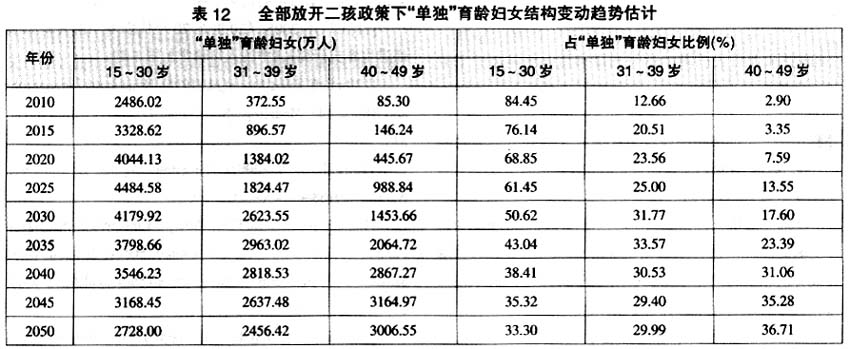
    其次，“单独”育龄妇女内部结构老化加速。若生育政策调整，那么由于低龄育龄妇女增加和低龄“单独”育龄妇女的减少，育龄妇女总体老化趋势将缓解，然而，仅从“单独”育龄妇女内部结构来看，若生育政策调整，由于低龄“单独”育龄妇女的减少，那么，“单独”育龄妇女内部老化将加速。2010～2050年40岁及以上的“单独”育龄妇女占“单独”育龄妇女的比例将由2010年的3％左右上升到2050年的36.70％左右(见表12)，比现行生育政策不变提高5％以上。但如果从全部育龄妇女来看，实际上40岁以上“单独”育龄妇女占全部育龄妇女的比例明显降低。通过表7和表8、表9和表10、表11和表12可以分别计算不同政策条件下40岁以上“单独”育龄妇女占全部育龄妇女的比例，并得到如果现行生育政策不变、“单独”放开二孩政策、全部放开二孩政策情况下，2050年40岁以上“单独”育龄妇女占全部育龄妇女的比例分别为15.1％、14.23％和11.52％。
    总之，生育政策的不同，不仅直接影响到未来“单独”育龄妇女规模和比例，而且影响到高峰的大小和比例的高低。现行生育政策不变和“单独”二孩生育政策条件下，30岁以上“单独”育龄妇女规模将持续上升，与此不同，全面放开二孩条件下，30岁以上“单独”育龄妇女规模将在2050年之前达到高峰后下降。无论是否调整生育政策，30岁及以下“单独”育龄妇女规模将在2050年之前都将达到高峰，只是高峰出现的早晚不同而已，现行生育政策不变和“单独”二孩生育政策条件下，30岁及以下“单独”育龄妇女规模高峰出现在2038～2040年，而全面放开二孩条件下高峰出现在2025年左右。
    四、主要结论
    随机微观人口仿真模型把研究视角从宏观转向微观，从个体转向家庭，从简单转向复杂，为人口系统仿真向社会系统仿真开辟了新的道路。本研究仅仅是随机微观人口仿真系统研究的一个很小的部分，除此之外它还可以用于很多实际问题的仿真研究，如教育、就业、社会保障和医疗卫生等。作为生育政策调整定量研究的一部分，本文通过小样本随机微观人口仿真分析得到以下基本结论：(1)虽然随机微观仿真非常复杂，但其突出优点是在样本量较小的情况下，计算机仿真结果与现有调查数据和宏观随机仿真模型比较具有高度一致性和可靠性，并可以获得比宏观模型更加丰富的研究信息。(2)“单独”育龄妇女总量在未来三四十年内持续快速增长的趋势不可逆转。(3)预计“单独”育龄妇女总量到2050年将是目前的2.8倍以上，占育龄妇女的比例也将达到30％以上。(4)“单独”育龄妇女的年龄构成将实现由目前的30岁及以下占绝对优势向30岁以上为主的结构转变，不同的生育政策对实现这一转变的影响不同。
    此外需要说明的是，由于本研究原始数据中并没有全部育龄妇女是否有兄弟姐妹的标识，因此一部分育龄妇女是否为“单独”育龄妇女是通过家庭成员关系匹配和模型估计的，因此，尽管年龄较大育龄妇女为独生女的可能性很小，但由于匹配误差和遗漏有可能低估近期内“单独”育龄妇女的总量。
    注释：
    ①“单独”育龄妇女指已婚育龄妇女本人或其丈夫为独生子女。
    ②对于随机人口预测模型可以参考Keilman，2001；Lee等，1994；Lee等，2001；Lutz等，2008；微观人口仿真模型的建模方法和实现过程可以参考Evert等，1995；李善同、高嘉陵，1999；杨耀臣，1999。
    参考文献：
    [1]方拴锋等(2010)：《独生子女与非独生子女心理健康状况分析》，《临床合理用药》，第10期。
    [2]风笑天(2008)：《中国独生子女问题：一个多学科的分析框架》，《浙江学刊》，第2期。
    [3]郭翠菊(2000)：《独生子女家庭教育的误区及其矫治》，《教育科学》，第4期。
    [4]姜全保、郭震威(2008)：《独生子女家庭丧子概率的测算》，《中国人口科学》，第6期。
    [5]李善同、高嘉陵(1999)：《微观分析模拟模型及其应用》，机械工业出版社。
    [6]齐险峰、郭震威(2007)：《“四二一”家庭微观仿真模型与应用》，《人口研究》，第3期。
    [7]宋健(2005)：《中国的独生子女与独生子女户》，《人口研究》，第2期。
    [8]肖富群、风笑天(2010)：《我国独生子女研究30年：两种视角及其局限》，《中州学刊》，第4期。
    [9]杨耀臣(1999)：《蒙特卡罗方法与人口仿真学》，中国科技大学出版社。
    [10]周长洪(2009)：《大量独生子女家庭将导致社会性养老困境》，《探索与争鸣》，第7期。
    [11]王广州(2005)：《20世纪70年代以来中国育龄妇女递进生育史研究》，《中国人口科学》，第5期。
    [12]Imhoff, Evert Van et al. (1995), Household Demography and Household Modeling. New York-London Plenum Press. 319-341.
    [13]Keilman N. (2001), Uncertain Population Forecasts. Nature. 421(6846): 490-491.
    [14]Lee R. D. , and S. Tuljapurkar(1994), Stochastic Population Projections for the United States: Beyond High, Medium and Low. Journal of the American Statistical Association. 89(428): 1175-1189.
    [15]Lee R. D. , and T. Miller(2001), Evaluating the Performance of the Lee-Carter Method for Forecasting Mortality. Demography. 38(4): 537-549.
    [16]Lutz W. , S. Sanderson, and S. Scherbov(2008), The Coming Acceleration of Global Population Ageing. Nature.451: 716-719.