我国通货膨胀路径中的结构性变化与非线性调整——基于TV-STAR模型的实证分析

    内容提要：本文使用TV-STAR模型研究发现，我国通货膨胀路径中结构性变化与非线性共存。结构性变化发生在1995年左右，结构性变化前的通货膨胀路径中存在高、低两个均衡点，结构性变化后的通货膨胀路径中存在唯一均衡点，但通货膨胀的持久性较变化前有较大幅度上升。同时发现通货膨胀与通货紧缩的非线性调整具有明显的非对称性，其临界值为4.091。基于广义脉冲响应函数发现，结构性变化后，我国通货膨胀对外来冲击的反应幅度下降，但反应速度上升。另外，正、负向冲击对通货膨胀的影响存在明显的非线性和非对称性。在多数情况下，正向冲击的影响更大，也更持久。在短期内，通货膨胀机制下的冲击影响要明显强于在通货紧缩机制下，但从长期来开，通货紧缩机制下的冲击影响更持久。在结构性变化之后，这种冲击的非对称效应也更明显。
关键词：TV-STAR模型/结构性变化/非线性调整/转换函数/广义脉冲响应作者简介：吴吉林，山东大学经济研究院，电子信箱：rainforestl061@gmail.com（济南250100）。
        一、引言
    正如Lucas（1976）所指出，宏观经济变量的计量模型参数并不是一成不变的。现有研究发现，在过去的几十年里欧美国家通货膨胀的动态路径发生了显著的变化。这些变化不仅表现在通货膨胀水平上，而且还表现在通货膨胀的持久性上（Kim，2000）。因此，预测通货膨胀率以及对通货膨胀建模也变得越发困难。通货膨胀的复杂性不仅体现在上述的结构性变化中，而且由于通货膨胀等宏观经济变量与经济周期密切相关，这使得通货膨胀动态变化中还包含了经济扩张与衰退的非线性特征（Beaudry and Koop，1993；Pesaran and Potter，1997）。货币政策的变化、需求与供给的冲击以及通货膨胀预期的变化也都可能引起通货膨胀的非线性。因此，在对通货膨胀建模时，可能需要同时考虑结构性变化与非线性等特征。然而，到目前为止，关于通货膨胀的所有研究都还是孤立地考察上述特征的某一方面，如，Evans和Watchtel（1993）基于机制转换模型发现，美国通货膨胀在20世纪70年代中期和80年代中期发生了两次较大的结构性变化。Burdekin和Siklos（1999）使用Perron和Vogelsand（1992）的结构断点检验法发现美国通货膨胀在1979年出现了较大的结构断点。另外，Enders和Hum（2002）使用门槛自回归TAR模型发现澳大利亚的通货膨胀率存在明显的非线性和非对称性。Martin和Milas（2004）基于平滑转换STAR模型研究发现英国货币政策对通货膨胀率的反应存在非线性，其强度取决于离通货膨胀目标值的距离。
    同样，国内学者也对我国通货膨胀的运动特征展开了研究，但也都是孤立地考察通货膨胀的结构性变化或非线性。其中，关于我国通货膨胀结构性变化的研究较少：刘金全等（2006）运用参数稳定性检验法，发现我国通货膨胀序列自1984年以来出现了两次高通货膨胀区间。张成思（2008）运用结构断点检验法考察了1981-2007年我国月度通货膨胀的动态变化，结果显示我国的通货膨胀路径在20世纪90年代中期发生了显著的结构性变化。而关于非线性研究的文献有：龙如银等（2005）运用Markov机制转换模型揭示出我国通货膨胀率存在两个区间，即高通货膨胀率区间和低通货膨胀率区间。赵留彦、王一鸣和蔡婧（2006）运用改进的Markov机制转换模型发现我国的通货膨胀率与通货膨胀不确定性间存在非线性性。王少平和彭方平（2006）运用ESTAR模型也发现我国通货膨胀和通货紧缩间存在非线性指数转换特征。张屹山和张代强（2008）在TAR模型的基础上研究我国通货膨胀的特点，实证结果表明，我国通货膨胀率是局部单位根的门槛自回归过程，在高通货膨胀下，通货膨胀率是平稳自回归过程；在低通货膨胀下，通货膨胀率是单位根过程。
    如果通货膨胀的动态过程中确实存在结构性变化与非线性调整这两种特征，只孤立地考察通货膨胀运动的某一特征将不能很好地揭示通货膨胀的真正本质。那么是否可以通过样本数据来内生地判定通货膨胀路径中是否同时存在结构性变化与非线性这两种特征，或者只存在其中一种特征，或者两种特征都不存在，这样就能避免模型的误设问题。Lundbergh等（2003）提出的时变平滑转换自回归（TV-STAR）模型能够很好地用来解决上述问题。该模型不仅能同时考察经济变量的结构性变化与非线性调整，并且能通过模型设定检验来区分这两种不同特征。另外，许多宏观经济变量的机制变化是逐步过程，Markov机制转换以及TAR模型等均假设机制间的转换较突然，因而不能描述机制的渐进变化过程。TV-STAR模型由于能通过转换参数来控制转换速度的大小，所以不仅能够刻画较突然的机制变化，也能刻画渐进形式的机制变化。正因为TV-STAR模型具有以上许多优良性质，因此被广泛用于研究经济、金融变量的运动特征，如Franses和Dijk（2005）比较了各类线性与非线性模型的预测效果，发现TV-STAR模型在长期中的预测效果要优于其他模型。Sollis（2008）使用TV-STAR模型检验了17个以美元为基础的经济发达国家汇率变动特征，发现一些国家的汇率变动中以结构性变化为主，而另一些国家的汇率变动中同时存在结构性变化与非线性调整。Hasanov等（2010）对土耳其的通货膨胀与产出间关系即菲利普斯曲线的研究表明，两者间存在明显的结构性变化与非线性调整。
    鉴于此，本文将通过引入TV-STAR模型来考察我国通货膨胀的动态特征，在统一框架下探索我国通货膨胀中的结构性变化与非线性调整。基于该模型的研究具有重要的经济与政策意义：我国的通货膨胀是否同时存在结构性变化与非线性？如果的确存在这两种特征，那么结构性变化发生的时间点在哪里，在结构性变化前后，通货膨胀的非线性特征是否也发生了变化？不同状态和结构下的我国通货膨胀持久性有何不同？正、负向外来冲击的影响也呈现非对称性吗？另外，我国通货膨胀与通货紧缩间的临界值是多少？对上述问题的研究将有助于加深对我国通货膨胀本质的了解，从而为治理通货膨胀提供一定的理论支持。本文将基于TV-STAR模型的实证分析结果来回答上述问题。余下部分安排为：第二部分为数据与模型；第三部分为实证分析；第四部分为结论与政策建议。
    二、数据性质与模型设定
    （一）数据性质与平稳性检验
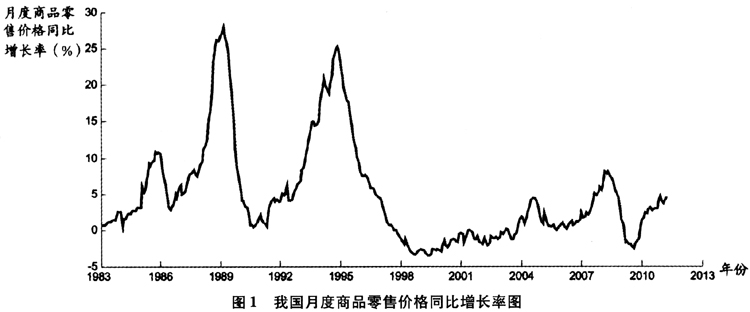
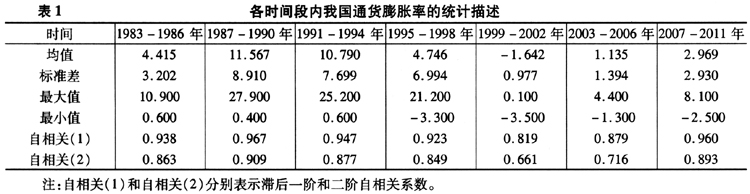
    本文使用商品零售价格同比指数增长率的月度数据来研究我国通货膨胀率的特征，样本范围从1983年1月至2011年3月，共计339个样本，数据来源于中经网数据库①。由于我们采用同比增长率，通货膨胀序列中已消除了季节因素的影响。图1给出了我国通货膨胀的动态路径图。总体来讲，从1983年1月至2011年3月的这段时间内，我国通货膨胀的变化呈现两种不同态势，在20世纪90年代中期之前，我国处在从计划经济向市场经济的转轨时期，经济运行极不稳定，通货膨胀的波动较大。从表1可以明显看出，1998年之前的通货膨胀无论从均值、标准差、最大值以及一、二阶自相关系数上，都明显要相对高于1998年之后的通货膨胀，并分别在1985年底、1989年初以及1994年底出现三次较大的峰值，后两次的通货膨胀率甚至超过了25%。在90年代中后期，由于市场价格形成机制的初步建立，我国经济成功实现了“软着陆”，在保持经济快速增长的同时，通货膨胀的波动区间也开始减小。但2008年次贷危机之后，随着各经济发达国家中央银行采用“量化宽松”的货币政策缓解市场流动性、刺激经济，世界范围的通货膨胀已经形成，通货膨胀预期明显增强。我国政府也实施了积极的财政政策和适度宽松的货币政策，但其结果是从2010年下半年开始，我国消费者价格指数一路攀升，截至2011年第一季度，我国CPI同比指数升至5.0%，治理通货膨胀再次成为全年经济的重中之重。
     
     
    许多基于ADF单位根的检验结果对我国通货膨胀率是否具有平稳性存在较大分歧，如赵留彦等（2005）发现我国通货膨胀率在某一时域内具有平稳性，而在另一时域内具有非平稳性；王少平和彭方平（2006）发现我国通货膨胀率是平稳的；而刘金全和隋建利（2010）发现我国通货膨胀率是非平稳的。出现上述分歧的可能原因是，传统线性模型的ADF单位根检验法由于存在功效（power）问题，会过度地接受原假设，从而使得检验结果不可靠（Taylor，2001）。另外，我国通货膨胀的持久性中可能存在非线性特征，传统检验法很难在线性单位根与非线性平稳序列间作出判别。为此，我们引入Kapetanios等（2003）提出的KSS非线性单位根检验法，该方法比ADF检验法更具有稳健性，并能检测出所有线性与非线性单位根过程：
     
    这时，可通过构造统计量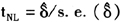来检验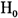：δ=0以及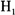：δ＜0，从而判断通货膨胀序列中是存在单位根还是具有非线性平稳特征。表2同时给出了ADF以及KSS的单位根检验结果，考虑到数据生成过程的各种可能，我们分别使用带常数以及带趋势的单位根检验。为了使得检验结果稳健，滞后阶数分别取4、8、12三个不同数值。KSS检验中10%和5%的渐近临界值摘自于Kapetanios等（2003），其分别为-2.66和-2.93。表2显示ADF检验的结果取决于滞后长度以及模型的具体设定形式，不能一致地判断我国通货膨胀率是否存在单位根；而KSS检验的所有结果均在5%水平上拒绝存在单位根。通过比较可以发现，ADF检验由于线性假设以及较低的功效，对我国通货膨胀率单位根的检验是无能为力的。而KSS检验能得出一致的检验结果。本质上我国通货膨胀率是平稳的非线性均值回归过程。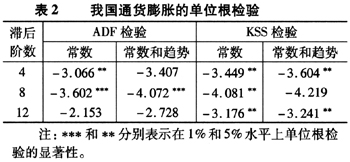
     
    （二）模型设定与检验
    TV-STAR模型是两机制STAR模型的一种推广，为了更好地了解TV-STAR模型的性质，我们首先介绍STAR模型。自从Terasvirta（1994）提出STAR模型以来，该模型就被广泛地用于研究宏观经济和金融变量的非线性动态特征，两机制STAR模型可描述为：
     
     
    1.确定AR（p）模型中的滞后阶数p，以及确定STAR、TV-STAR模型中的延迟参数d。
     
    由于上述建模步骤中涉及不可识别参数与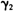，将使得假设检验变得复杂。处理这类问题的通常做法是，在原假设下对平滑转换函数进行一阶泰勒展开：
     
    （三）非线性脉冲响应函数分析
    另外，我们可通过脉冲响应函数来分析通货膨胀运动在外来冲击下的反应特征。传统脉冲响应函数不依赖于过去历史信息，在同等幅度的正负向冲击下具有对称性。但STAR、TV-STAR等非线性模型明显地依赖于过去历史路径，并且在不同机制状态下，其运动特征也不尽相同。因此，在非线性模型中使用传统脉冲响应函数将产生偏差。为此，Koop等（1996）提出了广义脉冲响应函数（GIRF），其脉冲响应不仅取决于历史状态、现期冲击的大小、正负方向还取决于未来时期的冲击。该函数以历史信息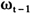为条件，是包括初始冲击δ与不包括初始冲击δ的两期望值之差：
     
    三、实证结果分析
    首先，基于线性AR（p）模型对通货膨胀率进行建模。通过自相关、偏自相关图以及结合AIC信息准则，我们选择AR（2）模型来刻画通货膨胀差分序列的动态过程。表3（见下页）显示，基于AR（2）模型的回归结果，我们发现残差部分具有非正态尖峰、厚尾等性质。另外，基于滞后4、8阶的Lung-Box检验虽未发现残差中存在自相关，但怀特检验发现残差中存在异方差效应。因此，从残差的诊断结果来看，AR（2）模型不是最优的，这可能是线性自回归模型不能捕捉通货膨胀中的非线性与结构性变化。
     
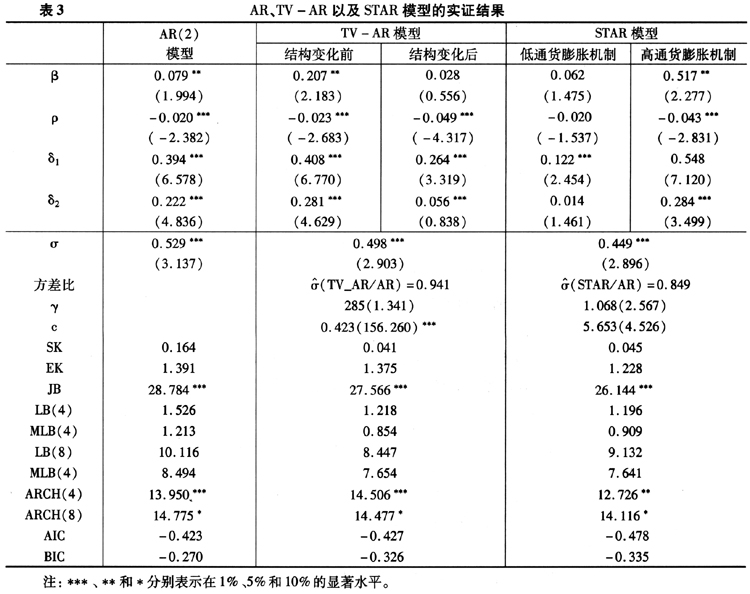
    为此，我们按照“从特殊到一般再到特殊”的过程来选择最优模型。基于TV-STAR模型，我们首先进行线性假设检验，即检验在TV-STAR模型与AR（2）模型之间，哪个能更好地描述我国通货膨胀率的运动过程。由于在模型的构建中，我们并没有考虑通货膨胀引起的异方差效应，其结果是，拉格朗日乘数（LM）检验在异方差下将可能过度拒绝或接受原假设。因此，我们同时给出了Wooldridge（1990）的具有异方差稳健性的LM检验统计量。通过使用普通的与稳健的LM检验将使得模型的估计和选择结果更加可靠。这里选取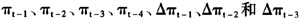作为平滑转换变量的备选变量。对于选择上述不同的转换变量，所有普通与稳健的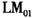检验的p值都较小，并且在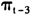时取得最小值，其在1%的显著水平上拒绝了模型的线性假设。
    虽然上述检验明显地拒绝了我国通货膨胀运动的线性假设，但我们仍不确定其运动过程是表现为非线性还是结构性变化，或是兼具两者特征。因此，我们开始在TV-STAR模型框架内检验我国通货膨胀的运动中是否只存在结构性变化而不存在非线性，即检验TV-AR模型是否能完全刻画我国通货膨胀的动态路径。TV-AR模型的回归结果显示（见表3），我国通货膨胀率约在1994年底至1995年初期间发生了较大的结构性变化。相对于线性模型，其标准差下降了5.9%，另外，偏度、峰度以及正态性也都有所改善，但异方差效应没有任何减少。从AIC和BIC信息准则上来看，TV-AR模型的拟合效果显然优于线性AR（2）模型。同样，基于普通与稳健的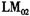模型设定性检验也在5%的水平上拒绝了TV-AR模型。因此，只单独考察我国通货膨胀的结构性变化是不合适的。
    我们再考察通货膨胀中是否只存在非线性变化而不存在结构性变化，即检验STAR模型是否能完全刻画我国通货膨胀的动态变化特征。在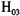的原假设下，可得两机制的STAR回归方程。两机制STAR模型由于假设不同机制下通货膨胀具有不同的运动特征，从而大大增加了模型的灵活性。STAR模型的回归结果显示，我国通货膨胀呈现明显的两机制运动特征，在高机制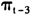（≥5.653）下，通货膨胀具有均值回归特征；而在低机制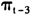（＜5.653）下，通货膨胀呈现局部单位根特征。最优转换变量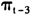中的d=3表明我国通货膨胀的调整发生在滞后3期，其调整的主要依据取决于通货膨胀是否过高或过低，并且调整的影响在三个月后起作用。相对于线性AR（2）模型来说，STAR模型的标准差降低了15.1%，从AIC与BIC两信息准则上来看，模型的拟合能力比起TV-AR模型也具有一定程度的提高。异方差效应得到了进一步改善，但仍旧不能消除。另外，基于偏度、峰度以及正态性检验的统计值也都有所改善。但表4的模型设定性检验显示，相对于TV-STAR模型，在5%的显著水平上无论是普通的还是稳健的LM统计检验量都拒绝了STAR模型。这表明，STAR模型不能很好地描述我国通货膨胀的运动特征，只单独考察我国通货膨胀中的非线性也是不合适的。
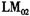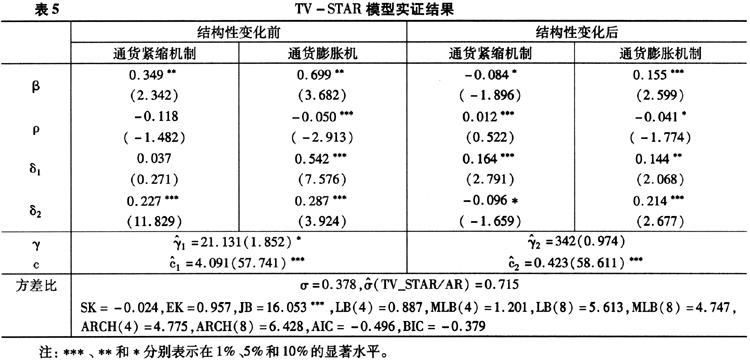
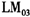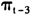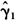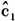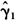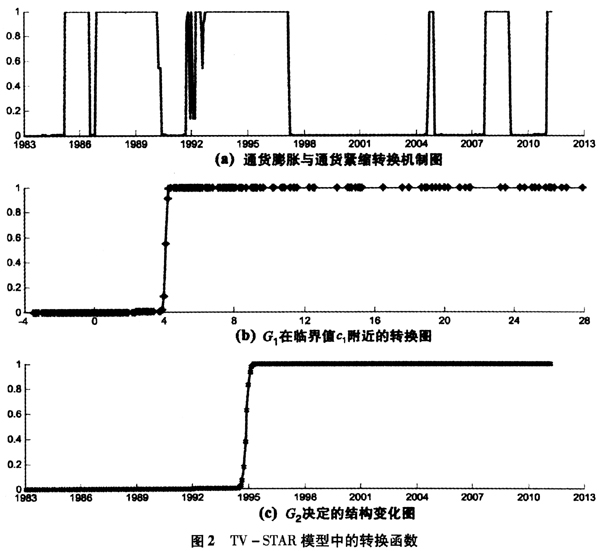
    上述和的检验结果显示，TV-AR模型和STAR模型都不能很好地描述我国通货膨胀的运动特征，忽略通货膨胀运动中的结构性变化或非线性都不合理。因此，我们开始在TV-STAR模型的框架内来同时考察我国通货膨胀的结构性变化与非线性运动特征。基于残差检验结果以及AIC和BIC信息准则来看，TV-STAR模型明显优于AR（2）、TV-AR以及STAR模型。特别是在TV-STAR模型下，回归残差的异方差效应已基本消失（见表5）。在转换函数G（，，）中，=21.131表明我国通货膨胀运动具有较快的非线性调整速度，另外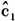，=4.091是我国发生通货膨胀与通货紧缩的临界水平值，这也反映在图2（b）中。相对于STAR模型而言，转换函数中的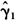有所上升，而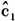有所下降，这可能是STAR模型由于未考虑结构变化而使得估计结果存在偏差的原因。由于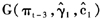为单调递增函数，在极端情形下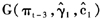，和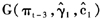分别对应着通货膨胀周期中的通货膨胀与通货紧缩。因此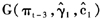，也刻画了我国通货膨胀与通货紧缩间的非线性调整特征，图2（a）明显地反映了我国通货膨胀运动的这一动态调整路径。结构性变化函数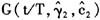中的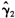=342表明我国通货膨胀的结构性变化较突然，并且该结构性变化点约在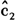=0.423左右，其对应的整个结构性变化样本时间范围约从1994年6月至1995年5月，历时1年左右，这从图2（c）中也可以明显地看出。结构性变化后通货膨胀的波动幅度出现了较大幅度的降低，该结构性变化与20世纪中期的货币政策以及财政政策的成功调整相一致，宏观经济政策的转变改变了模型参数的特征，并最终反映在通货膨胀运动路径的变化上。该发现也与张成思（2008）的结构变化检验法的研究结果相吻合。通过以上分析可以发现，在刻画我国通货膨胀的运动特征时，需同时考虑非线性以及结构性变化。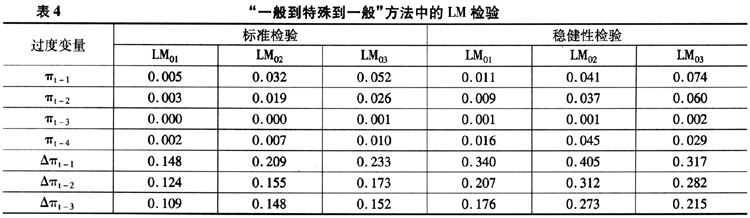
     
     
     
    通货膨胀的持久性反映了通货膨胀的运动惯性特征，其强弱一般是由自回归滞后系数的大小所决定，然而由于TV-STAR中△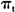的最大滞后阶数为2，即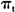的最大滞后阶数为3。在滞后阶数大于1时，通货膨胀的持久是由最大特征根决定。因此通过计算不同机制状态下的最大特征根，可用来比较通货膨胀的持久性特征。借助于TV-STAR模型，我们给出四个主要机制状态下的特征根，而通货膨胀的具体运动特征可视为在这四种状态下的转换组合。通过对最大特征根的比较不难发现，在过去二十多年时间里，我国通货膨胀的运动路径发生了明显变化：在1995年之前处在通货紧缩机制下即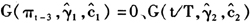时，最大特征根为0.804，这时通货紧缩的发生只是短期现象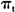，会很快恢复到正常水平；而1995年之前发生通货膨胀即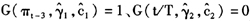时，最大特征根为0.929，该状态下的通货膨胀持久性要强于通货紧缩下的持久性，但影响仍旧会随时间而消去。与上述特征相反的是，在通货膨胀发生结构性变化之后，无论是处于通货膨胀还是通货紧缩机制下，持久性较结构性变化前都出现了上升。特别是当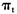处于通货紧缩机制下即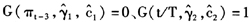时，最大特征根为1.013，这时πt基本表现为一单位根过程，通货紧缩具有非常强的持久性，甚至呈爆炸式扩张；而发生通货膨胀即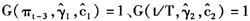时，最大特征根为0.932，此时的通货膨胀虽也表现出较强的持久特征，但该状态仍属于平稳状态，通货膨胀率会以较慢速度恢复至正常水平。总之，虽然结构变化后的通货膨胀的变动范围有较大下降，但通货膨胀和通货紧缩的持久性却明显上升。
    上述我国通货膨胀运动特征的这一变化也可通过进一步考察TV-STAR的确定性主干部分（不考虑随机冲击影响）来更深刻认识。如果模型确定性主干的外推开始于结构性变化之前（G（t/T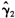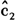，，）=0），在初始值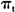≤4.091时，该模型将收敛于均衡点2.949；在初始值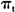＞4.091时，该模型将收敛于均衡点13.985。这表明结构性变化之前的通货膨胀虽具有全局稳定性，但具有局部非稳定性。相对而言，处于低均衡点2.949附近的运动基本不存在通货膨胀或通货紧缩的压力，即使出现通货紧缩压力，也很快能恢复至正常水平。而处于高均衡点13.985附近的运动，很难恢复至低均衡点，一旦处在高均衡点，通货膨胀将会一直维持较高水平，这也是1995年之前通货膨胀持续走高的原因。另外，如果模型确定性主干的外推开始于结构性变化之后（G（t/T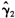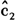，，）=1），无论初始值开始于何点，该模型都将最终收敛于全局唯一均衡点4.185，即收敛于临界值附近，这与稳健货币政策与积极财政政策的实施是密不可分的，特别是最近几年，中央政府把防止通货膨胀作为经济工作的重要任务之一，强化了货币政策特别是利率政策对通货膨胀预期的导向作用，从而使得通货膨胀率变动的不确定性下降。
    我们借助于广义脉冲响应函数，并基于结构性变化之前（G（t/T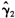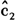，，）=0）、结构性变化之中（G（t/T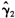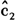，，）=0.5）以及结构性变化之后（G（t/T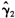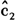，，）=1）的三个STAR模型来分别考察处于通货膨胀机制为主（G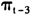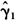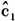（，，）＞0.5）和通货紧缩机制为主（G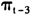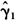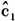（，，）＜0.5）时的我国通货膨胀运动对外来冲击的反应。这里冲击初始值设定为一单位的标准差即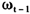，冲击期长h=1，2，…，40，基于历史信息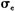和初始冲击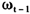的GIRF值可通过（6）式计算而得，期望值通过5000次的重复抽样计算而得。图3中的横坐标表示h，纵坐标表示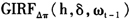。通过对比图3的（a）、（b）与（c），不难发现以下特征：首先，与结构性变化之前相比，结构性变化后的冲击影响幅度降低。当π处于通货膨胀机制下时，冲击效应几乎降低了50%之多，相对而言，当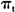处于通货紧缩机制下，冲击效应下降幅度相对较小。同时，冲击的传导效率上升。在通货膨胀机制下，冲击的最大反应期由结构变化前的第8期提前至第3期；而在紧缩机制时，变化最大的是负向冲击，其最大反应期由第15期提前至第2期。这种传导效率的极大提高从某方面也说明了我国市场体制改革的成功和资源配置方式转变的成功，使得各种来自于需求、供给以及货币的冲击能很快反映到价格的变化上来。由于传导效率的提高，任何的通货膨胀与通货紧缩迹象都能在较短时间内反映到作为市场信号的价格变化上，从而使得我国政府能依据价格信号对将要发生的通货膨胀与通货紧缩采取相应的经济措施，依据通货膨胀或通货紧缩的发展态势，综合应用汇率、利率以及其他货币政策手段对经济进行干预，因此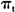的波动幅度也明显降低。其次，正向、负向冲击对通货膨胀的影响存在明显的非对称性，在多数情况下，正向冲击的影响更大，也更持久。而且通货膨胀机制下的冲击影响在短期内要明显强于通货紧缩机制下同等冲击的影响，但从长期来开，通货紧缩机制下的冲击效应更持久。在结构性变化之后，这种非对称效应也更加显著。这意味着我国更容易发生通货膨胀现象，即使出现了通货紧缩现象，但由于通货紧缩机制下的正向冲击更持久，而且作用也较强，因此，只要适当刺激经济，采取宽松货币政策，通货紧缩将很快消失。当在通货膨胀机制下，由于负向冲击的作用较小，而且持续时间较短，这就意味着，一旦发生通货膨胀，即使采取与通货紧缩机制下相反的同等强度的政策措施，但对抑制通货膨胀的效果不如通货紧缩机制下摆脱通货紧缩的效果好。通货膨胀与通货紧缩的这种非对称性特点使得治理通货膨胀的成本要远高于治理通货紧缩的成本。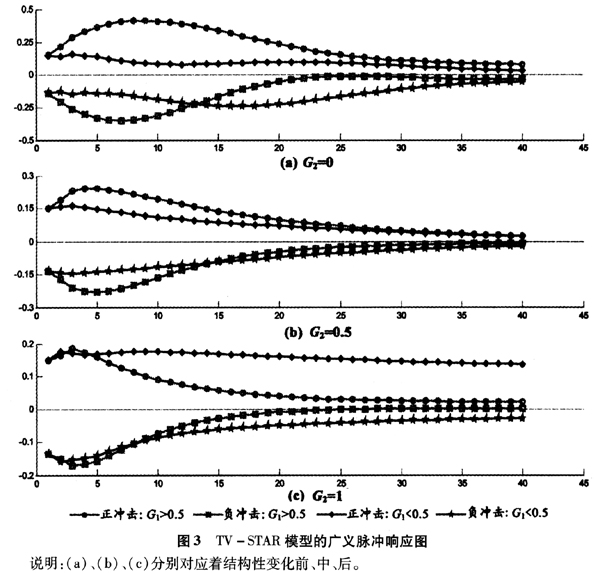
     
    基于通货膨胀与通货紧缩的临界值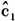=4.091，可以看出从2010年10月开始，我国存在明显的通货膨胀压力，由于此时通货膨胀机制下的最大特征根为0.932，因此高通货膨胀率将持续一段时间。此次通货膨胀与我国改革开放以来的历次通货膨胀均不同，其特点是：资产价格与普通商品价格的全面上涨，而且是由需求和供给两方面的因素共同推动而造成的。这些因素包括货币供应量过大而造成的流动性过剩、房价的泡沫化、能源价格、农产品价格的上涨。从图3（c）可知，由于通货膨胀机制下的正向冲击效应明显强于负向冲击，这也就是说，如果目前治理通货膨胀的力度不足，那么反通货膨胀的各种政策很可能被来自正向冲击如石油价格上涨、房价上涨等各种外部冲击效应抵消，而且由于同等的正向冲击效应更强也更持久，那么要降低当前的物价水平就非常困难。因此，我国政府在为控制通货膨胀而采取宏观调控政策的同时，需提防其他外来冲击而引发的对冲效应。
    四、结论及政策建议
    本文使用TV-STAR模型在统一框架内同时考察了我国通货膨胀的非线性调整与结构性变化，研究发现：
    首先，我国通货膨胀与通货紧缩之间存在明显的非线性转换，其临界水平为4.091，这种非线性调整具有非对称性，在不同的机制状态下具有不同的调整速度。由于20世纪80年代至90年代中期的经济体制转轨，货币政策、财政政策以及其他宏观经济政策也相应地经历了转变，这些调整使得我国的通货膨胀的路径在1994年下半年至1995年上半年间发生了结构性改变，结构性变化后的通货膨胀的波动幅度虽有较大幅度下降，但通货膨胀的持久性明显上升。
    其次，在结构变化前的通货膨胀路径中，存在高低两个局部均衡点，分别为13.985与2.949。当初始值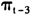＞4.091时，该模型将收敛于高均衡点；而当初始值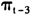＜4.091，该模型收敛于低均衡点。一旦通货膨胀的运动处于高通货膨胀机制下，通货膨胀将会在高均衡点附近运动，从而通货膨胀一直会维持在较高水平，这就解释了1995年之前持续发生高通货膨胀的原因。而结构性变化之后的通货膨胀路径中只存在唯一均衡点4.185，这就意味着1995年之后不再会发生持久的高通货膨胀或通货紧缩现象，通货膨胀变得更具有温和性，但持久性比结构变化前要更强。
    最后，结构性变化之后，通货膨胀的运动对外部冲击的反应幅度下降，但对冲击的反应速度上升，在某种程度也说明了市场的信息传递效率上升以及宏观调控政策的更加有效性。另外，在不同的机制下，同等程度的正负冲击对通货膨胀的影响存在明显的非对称性，在多数情况下，正向冲击要比负向冲击的影响更强、更持久。结构性变化之后，这种冲击的非对称效应也更明显。冲击的非对称效应使得治理通货膨胀的成本要高于治理通货紧缩的成本。
    在当前形势下，我国经济又处于高通货膨胀机制下，由于通货膨胀的持久性较强，而且来自石油价格上升、房价泡沫化以及美元快速贬值等压力的不确定性冲击，治理通货膨胀的难度较以往更大。因此，一方面我国要继续实施紧缩性货币政策，并严厉控制热钱的流入、逐步对人民币升值、扭转贸易顺差局面；另一方面，要加强财政政策与货币政策的协调配合，更多地发挥财政政策对结构调整、保障民生、促进就业等方面的支持力度，并逐步降低各种税率，降低企业的生产成本与投资成本。
    感谢匿名审稿人富有建设性的意见，但文责自负。
    注释：
    ①中经网数据库中商品零售价格同比指数（BPI）开始于1983年，而居民消费价格同比指数（CPI）开始于1990年。相对而言，CPI比商品零售价格能更好地作为通货膨胀率的代理变量，但为了从更长时间范围内考察我国通货膨胀路径的运动特征，我们选用了RPI。RPI与CPI间存在高度相关性，相关系数高达0.995，因此选用BPI具有合理性。刘金全等（2006）、张屹山和张代强（2008）也曾使用过RPI来研究我国通货膨胀率的运动特征。
参考文献：
        [1]刘金全、金春雨、郑挺国，2006：《我国通货膨胀率动态波动路径的结构性转变特征与统计检验》，《中国管理科学》第2期。
    [2]刘金全、隋建利，2010：《我国通货膨胀率及通胀膨胀不确定性的持续性和记忆性检验》，《吉林大学社会科学学报》第1期。
    [3]龙如银、郑挺国、云航，2005：《Markov区制转移模型与我国通货膨胀波动路径的动态特征》，《数量经济技术经济研究》第10期。
    [4]王少平、彭方平，2006：《我国通货膨胀与通货紧缩的非线性转换》，《经济研究》第8期。
    [5]张成思，2008：《通货膨胀动态路径的结构性转变及其启示》，《金融研究》第3期。
    [6]张屹山、张代强，2008：《我国通货膨胀率波动路径的非线性状态转换》，《管理世界》第12期。
    [7]赵留彦、王一鸣、蔡婧，2005：《中国通胀水平与通胀不确定性：马尔柯夫域变分析》，《经济研究》第8期。
    [8]Beaudry, P., and G. Koop, 1993. "Do Recessions Permanently Change Output?" Journal of Monetary Economics, 31(2): 149-163.
    [9]Burdekin, R. C. K., and L. S. Pierrre. 1999. "Exchange Rate Regimes and Shifts in Inflation Persistence: Does Nothing Matter?" Journal of Money, Credit, and Banking, 31(2): 235-247.
    [10]Evans, M., and W. Paul. 1993. "Inflation Regimes and the Sources of Inflation Uncertainty." Journal of Money, Credit and Banking 25(3): 475-511.
    [11]Enders, W., and A. Hums. 2002. "Asymmetric Price Adjustment and the Phillips Curve." Journal of Macroeconomics, 24(3): 395-412.
    [12]Franses, P. H., and D. van Dijk. 2005. "The Forecasting Performance of Various Models for Seasonality and Nonlinearity for Quarterly Industrial Production." International Journal of Forecasting, 21(1): 87-102.
    [13]Hasanov, M., A. Arac, and F. Telatar. 2010. "Nonlinearity and Structural Stability in the Phillips Curve: Evidence from Turkey." Economic Modelling, 27(5): 1103-1115.
    [14]Kapetanios, G., Y. Shin, and A. Snellb. 2003. "Testing for a Unit Root in the Nonlinear STAR Framework." Journal of Econometrics 112(2): 359-379.
    [15]Kim, J. Y. 2000. "Detection of Change in Persistence of a Linear Time Series." Journal of Econometrics, 95(1): 97-116.
    [16]Koop, G., M. H. Pesaran, and S. M. Potter. 1996. "Impulse Response Analysis in Nonlinear Multivariate Models." Journal of Econometrics, 74(1): 119-147.
    [17]Lin, C. J., and T. Tersvirta. 1994. "Testing the Constancy of Regression Parameters against Continuous Structural Change." Journal of Econometrics, 62(2): 211-228.
    [18]Lucas, R. 1976. "Econometric Policy Evaluation: A Critique." In The Phillips Curve and Labor Markets, ed. K. Brunner and A. Meltzer, 19-46. Carnegie-Rochester Conference Series on Public Policy, 1, New York: American Elsevier.
    [19]Lundbergh, S., T. Tersvirta, and D. van Dijk. 2003. "Time-Varying Smooth Transition Autoregressive Models." Journal of Business and Economic Statistics, 21(1): 104-121.
    [20]Martin, C., and C. Milas. 2004. "Modelling Monetary Policy: Inflation Targeting in Practice." Economica, 71(282): 209-221.
    [21]Perron, P., and T. J. Voglesang. 1992. "Nonstationarity and Level Shifts with an Application to Purchasing Power Parity." Journal of Business and Economic Statistics, 10(3): 301-320.
    [22]Pesaran, M. H., and S. M. Potter. 1997. "A Floor and Ceiling Model of US Output." Journal of Economic Dynamics and Control, 21(5): 661-695.
    [23]Sollis, R. 2008. "U. S. Dollar Real Exchange Rates: Nonlinearity Revisited." Journal of International Money and Finance, 27(5): 516-528.
    [24]Taylor, A. M. 2001. "Pitfalls for the Purchasing Power-Parity Puzzle? Sampling and Specification Biases in Mean-Reversion Tests of the Law of One Price." Econometrica, 69(2): 473-498.
    [25]Tersvirta, T. 1994. "Specification, Estimation, and Evaluation of Smooth Transition Autoregressive Models." Journal of the American Statistical Association, 89(425): 208-218.^