非参数随机条件持续期模型及其迭代算法

内容提要：随机条件持续期（SCD）模型能有效刻画超高频时间序列中持续期的变化，但该模型假定期望持续期生成机制固定，且模型参数估计存在一定的困难。文章在不假定条件均值形式和冲击项分布的基础上结合核估计方法提出了非参数SCD模型及其迭代求解方法。然后，基于TEACD（1，1）模型生成的模拟数据，将非参数SCD模型与用卡尔漫滤波进行伪似然估计的参数SCD模型和用Gibbs抽样进行马尔科夫蒙特卡罗估计的参数SCD模型的拟合效果进行比较，实证表明在大样本条件下非参数SCD模型的拟合效果与用MCMC估计的参数SCD模型的拟合结果相差不大，但明显优于用QML估计的参数SCD模型的拟合结果，且非参数SCD模型能为参数SCD模型的参数设定提供参考。
    关键词：SCD模型持续期伪似然估计MCMC估计核估计
    作者简介：孙艳（1984-），女，江苏泰州人，2010年3月毕业于东南大学获运筹学与控制论专业硕士学位，现为东南大学经济管理学院在读博士生，研究方向为高频数据建模；何建敏（1956-），男，江苏无锡人，现为东南大学经济管理学院博士生导师，教授；周伟（1983-），男，湖南益阳人，2010年3月毕业于南京航空航天大学，现为东南大学经济管理学院在读博士生。
    一、引言
    金融市场中数据的离散采集必然会造成信息不同程度的损失。无疑，采集频率越高，丢失的信息越少；反之，信息丢失得越多。计算机和通信技术的飞速发展，使得实时交易数据即超高频数据的采集成为可能。传统的对时间序列的建模是建立在假设交易时间间隔相等的基础上，但实际中并非如此，交易时刻是随机到来的，不可能是固定间隔的。交易活跃时，一秒钟内会有多笔交易；交易不活跃时，两笔交易之间会间隔几分钟甚至十几分钟。所以，对在等时间间隔假设基础上建模并应用得非常成功的SV（Stochastic volatility）模型和GARCH模型已不再适用。Engle和Russell在文献[1]中对交易间隔的条件分布构建了ACD（Autoregressive conditional durations）模型的雏形形式。1998年Engle正式提出ACD模型，其核心思想是用随机标值点过程去刻画交易过程[2]。Engle和Russell利用ACD模型研究不等时间间隔的交易的统计特征，并很好地预测了外汇交易价格询价的变化频率[3]。鉴于ACD模型对持续期拟合和预测的有效性，一系列学者对ACD模型进行了扩展研究。扩展主要从两个方面进行，一是对冲击项分布的选取用更复杂的Weibull分布、广义Gamma分布或者布尔分布来代替原先的指数分布；另一方面是对ACD模型中的条件均值方程的形式进行改进，如对数ACD模型、门限ACD模型、分整ACD模型等[4-7]。
    Bauwens和Veredas在2004年提出的SCD（Stochastic conditional durations）模型就是对ACD模型的重要扩展研究之一，其保留了ACD模型的基本特征，在条件均值方程中又引入一个潜在随机变量，用来捕捉市场中难以观察到的随机信息流。由于潜在随机变量服从白噪音过程，所以条件期望持续期就可能是负值，为了避免这种情况出现，条件均值方程采取对数形式[8]。该模型是一个双随机过程，一方面针对可观测的持续期，有一个随机扰动；另一方面对于不可观测的持续期的条件期望的对数，它也是一个随机过程。Feng受其启发研究了具有“杠杆效应”的SCD模型[9]。耿克红从理论上探讨了SCD模型和ACD模型与ARMA模型之间的关系，指出两类模型均可转化为ARMA模型，具有一定的相通性。并且实证了SCD模型在拟合金融市场超高频数据时比ACD模型更具优势[10]。
    与ACD模型不同的是，SCD模型的条件均值是由一个不可观测的随机过程决定的，从而导致其似然函数难以得到显式的形式，模型的估计非常困难。许多学者对模型的参数估计方法进行了探讨，如伪极大似然估计法（Quasi-maximum likelihood）、基于贝叶斯推断的马尔科夫链蒙特卡洛法（Markov chain Monte Carlo）、经验特征函数法（Empirical characteristic function）和广义矩方法（Generalized method of moments）[11-14]。所有这些参数估计方法都是建立在对条件均值方程的设定基础上，这样难免会导致模型设定的误差。
    文章利用非参数估计方法，借鉴Buhlmann等人建立非参数GARCH模型的思想[15]，构建了非参数SCD模型。非参数SCD模型假定条件期望持续期的对数函数形式为一个完全的非参数函数，这个非参数函数的自变量为对数条件期望的滞后值与服从白噪音过程的随机变量。对于针对持续期的随机扰动，只是假定相互独立，而不设定其服从某种分布。利用数据找到最符合自身的函数形式，再用估计的条件期望持续期的误差来分析冲击项分布选择的问题，这样可以得到比较符合数据本身特点的残差密度分布。对于参数SCD模型，其均值方程的生成机制固定，分别用卡尔漫滤波进行伪似然估计和Gibbs抽样进行MCMC估计。文章基于TEACD（1，1）模型产生的模拟数据，比较了参数SCD模型和非参数SCD模型的拟合效果。结果表明非参数SCD模型的拟合结果与MCMC估计的参数SCD模型的拟合结果相近，但明显优于QML估计的参数SCD模型的拟合结果。这主要是因为非参数SCD模型对对数条件期望的函数形式与随机误差项的分布形式不作更多的要求，因此在模型误设上就没有参数SCD模型敏感。研究还发现，非参数SCD模型的估计结果能对参数SCD模型的参数设定给予参考。
    二、参数SCD模型及其估计方法
    （一）参数SCD模型
    
    要求参数β满足|β|＜1是为了保证回归过程的平稳性。对数条件均值方程表示金融市场上持续期的聚类性，|β|越大，说明持续期具有越强的聚类性。
    
    式（1）-（2）具体描述了交易持续期的生成机制，式（2）中引入了一个产生条件期望持续期对数的随机过程，也因如此，该随机过程可以捕捉到金融市场上的很难直接观察到的随机信息流，较已有的自回归条件持续期ACD模型更为适用。
    （二）参数SCD模型的极大伪似然估计方法
    关于参数随机条件持续期模型的估计方法已有一定的研究成果，如GMM，ECF和MCMC等。Bauwens和Veredas在其文章中用卡尔漫滤波进行伪似然估计[8]。因为SCD模型能等价地转换为状态空间方程模式，其主要优点在于能将不可观测的变量（对数条件期望持续期）并入可观测模型（实际持续期），并且用功能强大的Kalman迭代算法得到估计结果。其具体计算方法如下：
    首先，通过对式（1）作对数变换，可以得到如下式（4）。
    
    以上就完成了整个参数随机条件持续期模型的构建和QML估计。此方法简单易实现，可以为模型参数的设定提供参考。不过在状态方程中，为了便于估计，假定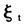近似服从正态分布，存在一定的结构性误差，也导致了估计结果的粗糙。
    （三）参数SCD模型的MCMC估计方法
    MCMC估计方法是近十几年来引入到计量经济领域一种新的行之有效的Bayes计算方法，尤其擅长处理密度函数分布是复杂的、高维的、混合的非标准形式的分布。其基本原理是通过建立一个具有平稳分布的Markov链来得到样本，再基于这些样本作出各种统计推断。最简单、应用最广泛的MCMC方法是Gibbs抽样，根据贝叶斯原理以及具体的模型计算出参数的条件密度函数，根据条件密度函数对相应的参数进行抽样，从而得到参数统计意义上的后验估计值。
    从模型（1）-（2）可以看出，只有持续期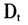｛｝是可观测值，而对数条件期望持续期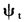｛｝是不可观测变量，连同模型参数（γ，α，β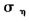，）都可以通过各自的后验条件分布进行抽样得到估计值。根据贝叶斯公式，可以分别计算出各个参数的后验密度函数。
    1.α的后验密度分布
    
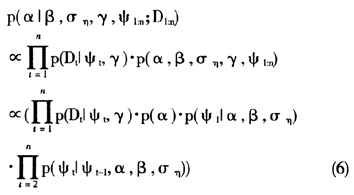
    2.β的后验密度分布
    
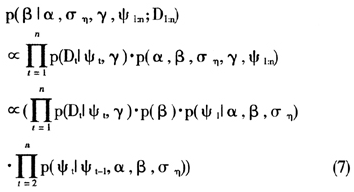
    3. 的后验密度分布
    
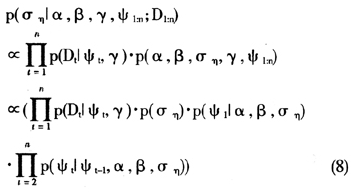
    4.γ的后验密度分布
    
    根据式（1）-（2），可以得出：
    
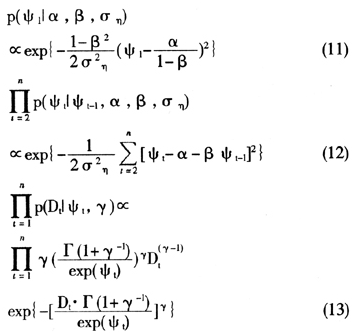
    根据Strickland和Forbes的观点[12]，选取如下分布作为α，β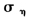，，γ的经验分布：α～N（0，1），β～Be（15，1.5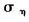），～IG（2.5，0.25），因为γ必须满足大于0的条件，选择对数正态分布logN（0，1）作为其经验分布。至此，条件密度分布（6）-（10）的所有显式形式都已得出。
    算法步骤
    步骤一：根据后验密度函数（6）对α进行抽样；
    步骤二：根据后验密度函数（7）对β进行抽样；
    步骤三：根据后验密度函数（8）对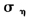进行抽样；
    步骤四：根据后验密度函数（9）对γ进行抽样；
    步骤五：根据后验密度函数（10）对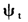（t=1，2，…，n）进行抽样；
    
    不难发现，SCD模型在引入随机变量描述随机信息流的同时，条件密度函数形式变得复杂，也为其模型参数的估计带来了不便。在常用的两种估计方法——QML和MCMC方法中，QML方法虽然在状态方程转换中存在一定的结构性误差，但实现简单；MCMC方法对于较为复杂的混合密度函数较为适用。同时，两种方法都是假定持续期以及期望持续期生成机制的固定性，而现实中往往难以得到的是变量间的相互关系，无法用具体的函数形式表示，方程的不确定性也就导致了QML方法中的状态方程无法得出、MCMC方法中的后验分布无法用显式表示。针对这个问题，文章在下文中通过借鉴非参数GARCH模型的思想[15]，提出了非参数SCD模型，并进一步构建了该模型的迭代算法。
    三、非参数SGD模型构建及其迭代求解方法
    （一）非参数SCD模型的构建
    
    （二）基于核估计的非参数SCD模型迭代求解方法
    结合Buhlmann和McNeil在研究GARCH模型的非参数形式时提出的迭代求解思想，文章对非参数SCD模型的求解构建如下的迭代求解方法。
    对式（14）进行恒等变形如下：
    
    算法中每一步迭代所采取的非参数回归方法是局部二元线性估计，原因在于其简单易操作，且不必修正边界。局部二元线性估计的原理如下：
    
    
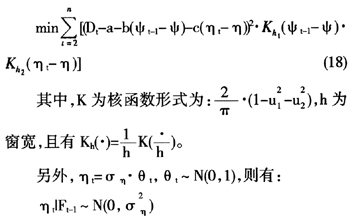
    步骤五：令k：=k+1，若k=K，停止；否则，返回步骤三。这里的K是使估计比较稳定的取值。
    由上述五个步骤共同构成了非参数SCD模型的迭代求解方法，关于方法的收敛性证明可以具体参考文献[15]中关于非参数GARCH模型的迭代算法收敛性的证明，虽然存在一定的差异但证明方法类似，文章将不再阐述。
    四、数据模拟与模型比较
    考虑到SCD模型与ACD模型的同质性，文章使用式（19）所示的参数TEACD（1，1）模型产生2100个模拟数据，为了避免初值的影响，剔除前100个数据，取接下来的2000个数据，样本容量为2000。分别作参数回归和非参数回归，并对这两个模型的拟合效果进行比较。
    
    具体的分析和计算过程如下：
    对上述2000个模拟数据进行基本统计分析，分析结果如表1所示。
    
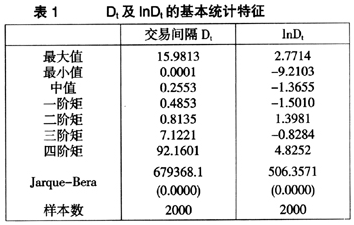
    由上表可知，模拟数据的交易间隔的最大值为15.9813秒，最小值仅为0.0001秒，其中中值为0.2552，标准差为0.8135。下面首先对SCD模型分别进行QML估计、MCMC估计和非参数估计，再进一步比较它们的拟合结果。
    （一）参数SCD模型的QML估计
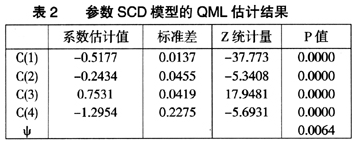
    对根据式（1）-（2）的参数SCD模型转化的状态空间方程（5），利用Kalman滤波进行伪似然估计，以上伪似然估计的过程可通过EVIEWS软件求得，具体结果如表2所示。
    
    对应式（5）有c（1）=-0.5772/γ，从而：
    γ=-0.5772/-0.5177=1.1148
    
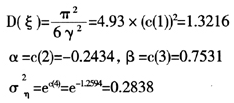
    根据表2的参数估计结果可知：所有参数的P值均通过假设检验，ψ的P值仅为0.0064，均满足置信度为1%的要求，模型计算效果较好。
    
    最后利用MSE和MAE公式对参数SCD模型QML估计方法的拟合效果进行计算，并得两种拟合误差分别为：
    MSE=1.6476：MAE=0.6155
    （二）参数SCD模型的MCMC估计
    参数SCD模型的MCMC估计方法可用Winbugs软件实现。为了从多方面获取待估参数的后验估计值，文章在程序中分别设定了均值、2.5%分位数、97.5%分位数以及方差来描述参数的统计性质，结果如表3所示。
    
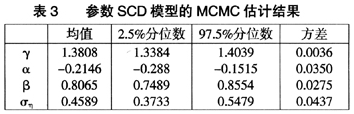
    因为模拟数据由式（19）产生，单从参数SCD模型的估计值，并不能得出这两种估计方法的优劣。为了便于统一，文章根据MCMC估计法所得的模型，同样比较其拟合效果，具体如下：
    MSE=1.2379：MAE=0.4370
    根据结果可以看出，相比QML估计方法所得的拟合误差有一定程度的优势，这不仅因为QML估计过程中所作的正态分布的假设存在一定的结构性误差，也因为MCMC估计方法是根据模型结构和数据本身所作的后验估计，且基于平稳分布的马尔科夫链蒙特卡罗模拟是收敛的。
    （三）非参数SCD模型的估计
    
    计算中窗宽h的选择对于估计的效果非常重要，文章在计算中采取了认可度较高的经验法，其选用步骤为：首先看数据的大致取值范围，给定一个窗宽，然后不断调整，直到所选择的窗宽使得所得的结果比较满意为止。
    
    
    算法中设定的终止条件为相邻两步迭代的MSE误差相差为0.01，用Matlab编程实现。迭代结果如表4所示。
    
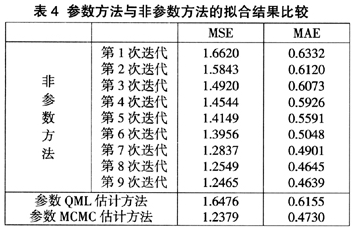
    观察表4可得以下结论：（1）文章中提出的非参数SCD模型的迭代算法具备收敛性，该算例中迭代算法从第二次迭代开始逐步趋于收敛。（2参数SCD模型的MCMC估计方法的拟合结果明显优于QML估计方法的拟合结果，这便是精度与时间复杂度的取舍。（3）非参数SCD模型的拟合结果与参数SCD模型的MCMC估计方法的拟合结果平分秋色，且两种方法在时间复杂度上也旗鼓相当。另外，非参SCD模型及其迭代算法一般不需要假定期望持续期的方程形式，更具备一般性，所以不失为另外一种可供选择的比较优良的方法。
    以上的算例是从大样本的角度出发对参数SCD模型和非参数SCD模型进行计算比较，作者在具体的模型研究中还使用了多组小样本数据进行了参数和非参数SCD模型的计算和比较，发现：在小样本的情况下参数SCD模型与非参数SCD模型优劣程度不一，非参数SCD模型的拟合结果不太稳定。不过，在一般的金融时间序列中遇到的样本一般属于大样本，因此非参数SCD模型具备较大的应用空间。
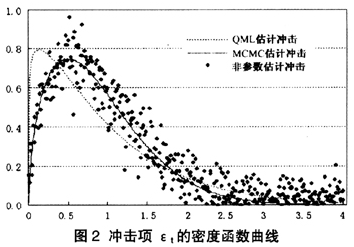
    另外，在对非参数SCD模型进行具体计算中还发现：根据实际持续期与期望持续期得到的误差项的密度函数如图2中的虚线所示，虚线是威布尔分布W（1.1148，1）的密度函数曲线，实线是威布尔分布W（1.3808，1）的密度函数曲线，散点是根据由非参数SCD模型计算拟合持续期与期望持续期比值得出的冲击项分布。三条曲线的形状和位置都比较相似，但是，非参数方法得到的关于误差项的分布与由MCMC估计得到的误差项分布更贴近些。因此，据非参数估计所得的冲击项分布可以为参数SCD模型的设定提供参考意见。
    
    五、结束语
    SCD模型是对交易到达时间间隔即交易持续期建模，可用来验证定性的市场微观结构理论，也可以用于金融市场风险定量分析。
    针对已有的参数SCD模型的极大伪似然估计方法存在的结构性误差以及参数SCD模型中对数条件期望持续期产生机制固定这两方面问题，文章在参数SCD模型的基础上，既不假定冲击项的分布，也不假定条件期望持续期的函数形式，构建了非参数SCD模型，并借鉴非参数GARCH模型的求解方法提出了非参数SCD模型的迭代算法，让其找到最符合数据本身的函数形式和误差项分布。最后，文章通过参数TEACD（1，1）模型模拟的大样本数据，将参数SCD模型分别运用QML方法和MCMC方法进行估计，将这两种方法的拟合结果与非参数SCD模型的拟合结果进行比较，并得出结论：在大样本的情况下非参数SCD模型的拟合结果与基于贝叶斯推断的MCMC估计的参数SCD模型拟合结果相差不大，但明显优于QML估计的参数SCD模型的拟合结果。并且，非参数SCD模型的估计能为参数SCD模型冲击项分布函数的选择以及条件均值方程的设定提供参考。
    人们对SCD模型族的研究还处于刚刚起步阶段，非参数SCD模型及其求解方法的研究为金融市场上关于持续期的（超）高频数据分析与建模提供了一个有效的途径，也是基本SCD模型的扩展之一。但是就模型本身的扩展仍然不够，在随后的研究中将对SCD模型的扩展作进一步探讨。
    参考文献：
    [1]Engle R. F., Russell J. R. Forecasting Transaction Rates: The Autoregressive Conditional Duration Model[R]. NEBR Working Paper 4966, 1994.
    [2]Engle R. F., Russell J. R. Autoregressive Conditional Duration: A New Model for Irregular-Spaced Transaction Data[J]. Econometrica, 1998(66): 1127-1162.
    [3]Engle R. F., Russell J. R. Forecasting the Frequency of Changes in Quoted Foreign Exchange Prices with the Autoregressive Conditional Duration Model[J]. Journal of Empirical Finance, 1997(4): 187-212.
    [4]Bauwens L., Giot P. The Logarithmic ACD Model: An Application to the Bid-Ask Quote Process of Three NYSE Stocks[R].Université Catholique de Louvain, 2000.
    [5]Zhang M. Y., Russell J. R., Tsay R. S. A Nonlinear Autoregressive Conditional Duration Model with Application to Financial Transaction Data[J]. Journal of Econometrics, 2001(104): 179-207.
    [6]Jasiak J. Persistence in Intertrade Durations[J]. Finance, 1998(19): 166-195.
    [7]Fernandes M J, Gramming, J. A Family of Autoregressive Conditional Duration Models[Z]. Working papers, Graduate School of Economics, Getulio Vargas Foundation(Brazil), 2003.
    [8]Bauwens L., Veredas D. The Stochastic Conditional Duration Model: A Latent Variable Model for the Analysis of financial durations[J].Journal of Econometrics, 2004(119): 381-412.
    [9]Feng D. G., Jiang G. J., Song P. Stochastic Conditional Duration Models with "Leverage Effect" for Financial Transaction[J]. Journal of Financial Econometrics, 2004, 2(3): 390-421.
    [10]耿克红，张世英.SCD模型与ACD模型比较研究[J].管理学报，2008，5(1)：44-48.
    [11]Sandmann G., Koopman S. J. Estimation of Stochastic Volatility Models via Monte Carlo Maximum Likelihood[J]. Journal of Econometrics, 1998(87): 271-301.
    [12]Strickland C. M., Forbes C. S., Martin G. M. Bayesian Analysis of the Stochastic Conditional Duration Model[J]. Computational Statistics & Data Analysis, 2006, 50(9): 2247.
    [13]Cho S. A linear Bayesian Stochastic Approximation to Update Project Duration Estimates[J]. European Journal of Operational Research, 2009, 196(2): 585-593.
    [14]Knight J., Ning C. Q. Estimation of the Stochastic Conditional Duration Model via Alternative Methods[J]. Econometrics Journal, 2008(11): 593-616.
    [15]Buhlmann P., McNeil A. J. An Algorithm for Nonparametric GARCH Modeling[J]. Computational Statistics & Data Analysis, 2002(40): 665-683.
    [16]李竹渝，鲁万波，袭金国.经济、金融技术计量学中的非参数估计方法[M].北京：科学出版社，2007.^