高维模型选择方法综述（四）

4.4误选率法
    误选率法是由Wu等[51]针对向前选择法调整参数的选取而提出的，可推广到更多的模型选择方法。向前选择法中，选入标准α即为调整参数。通常选入标准是由分析人员主观设定的，一般取值为0.05或0.1。在给定已选入变量的条件下，因变量对每个不在模型中的候选变量建立回归，并做显著性检验，若P值最小值小于该水平，则相应变量被选入到模型中。越大的α值对应于越宽松的选择准则，最终的模型也会包含越多的变量。特别地，α=1时，选择模型为全模型。但在有的情况下，我们关心的不是选择模型是否包含所有真实的变量，而是选择模型中不含信息的变量比例是否被控制住。误选率方法就是从这个角度入手，在选择模型误选率不超过事先设定误选率的前提下，选择调整参数使选择模型达到最大。
    最初的误选率法是将一些噪音变量人为地加入到设计矩阵中，通过观察他们在向前选择过程中进入模型的情况，来选取合适的调整参数[52]。Wu等[51]最初产生噪声变量的方法是将解释变量的观测随机打乱，从而与因变量失去对应关系，可看做噪声。但是当样本量较小的时候，这样产生的噪声变量还会与原变量有相关性，可以令每个产生的变量对原变量进行回归，利用残差作为噪声变量。那么，新的噪声变量与响应变量独立，与原变量无相关性，且满足样本均值为零。选择模型的误选率的表达式为
    
    其中期望是关于真实模型的重复抽样而言的，U（α），I（α）分别表示调整参数取值α时选择模型中无信息变量数和有信息变量数，S（α）=U（α）+I（α）是选择模型的变量数，p是全部自变量的数目，p-S（α）是未被选入最终模型的变量数，是对全模型中无信息变量数目的一种估计。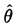（α）是无信息变量进入模型的比例的估计，是由噪声变量估计的，即
    
    Chen[54]对误选率法做了推广，从向前选择法调整参数选择推广到一般的Cox模型时的调整参数选择。例如在LASSO方法中，λ连接似然项和惩罚项，其取值越大，模型越稀疏。这与向前选择中α的功能类似，因此引入如下变换统一二者
    
    其中c＞0为常数，文中建议使用c=0.005。类似于普通误选率法，Chen[54]给出了应用于LASSO等方法的调整参数选择算法。这种方法的性质及与其他调整参数选取方法的比较可以参考Chen[54]。
    4.5稳定路径法
    稳定路径选择法是一种将二重抽样和选择算法相结合的模型选择方法，之所以将其归为调整参数选择而非模型选择方法，是因为该方法不能单独使用，而是需与已有的模型选择方法如LASSO等配合使用。读者可参看Meinshausen和Buhlmann[55]。稳定路径法可将一般的调整参数选取问题转化为对调整参数不敏感的模型选择问题，进而绕开这个棘手的问题。除此之外，稳定路径法还可以提高已有选择方法的相合性。
    
    其中被选概率的阈值0＜π＜1是新的调整参数。Meinshausen和Buhlmann[55]中的模拟数据例子表明，稳定路径法能明显地区分有信息变量和无信息变量的路径，概率阈值这个调整参数对最终模型选择结果的影响很小，并不像原模型选择方法中的调整参数那样敏感。同时，该方法对于原调整参数λ的取值域Λ依赖性也很弱，只要其取法不是太偏激，对最终结果影响不大。特别地，若受限于计算能力，只能对单一的λ进行稳定路径分析（此时每条路径退化为一个点），只要λ选取的适当，也是可以的。
    稳定路径选择法的计算成本与用交叉验证选取调整参数的模型选择方法相差不多甚至更低。以LASSO方法为例，其时间复杂度为O（npmin｛n，p｝）。在样本量小于变量数的情形下，用一半样本做模型选择的时间是用全体样本进行计算的时间的1/4。一般稳定路径法重抽样进行100次即可。那么对于给定的单一调整参数λ，稳定路径法实现变量选择只需要25倍LASSO运算时间。而若用十重交叉验证选取调整参数，对于每个候选调整参数λ，大概需要10倍LASSO运算时间。由此可得，对单个调整参数，稳定选择法的计算成本大概是交叉验证法的2-3倍。但是注意到稳定路径法并不需要穷举调整参数集Λ的所有元素（不同调整参数对稳定路径选取结果影响不大），因此其计算成本通常低于交叉验证。
    稳定路径法最大的优势有两条：一是当调整参数的选取因数据噪声水平未知而变得非常困难时，该方法可以使得模型选择的结果对调整参数变得不敏感；二是通过使用该方法可以使原本不具备相合性的模型选择方法具有相合性。有兴趣的读者可参考Meinshausen和Buhlmann[55]。
    5结论和未来研究
    高维模型选择是当代统计学领域的研究热点，在实际中具有广泛的应用价值。本文以线性模型为切入点，重点介绍了LASSO方法及用于特定情形的衍生惩罚因子模型选择方法，详细描述了DS方法、降维回归方法等，并细致讨论了模型选择过程中调整参数的选取问题。随着新思想的不断出现，模型选择的理论方法日益丰富，为解决实际问题提供了多种选择。
    总的来说，模型选择最关注两个问题：一是选择模型的预测准确性，又称有效性；一是选择模型与真实模型的相合性，也可称为可解释性。例如在惩罚因子模型选择法中，NG方法、LASSO方法、EN方法等属于预测指向型方法；而Adaptive LASSO、SCAD方法等则属于解释指向型的范畴。调整参数的选择方法多依据交叉验证的思想得来，如舍一验证、广义交叉验证、广义近似交叉验证等都是典型的预测指向型方法；但也有少数方法如B类广义近似舍一验证、稳定路径法等从选择模型的相合性角度选取调整参数，因而属于解释指向型方法。在处理实际问题时，应根据实际需要选取相应的方法。
    模型选择的未来发展将主要集中在如下的几个方面：
    1）不同模型选择方法的比较与关联。目前的模型选择方法多种多样，方法之间缺乏横向比较，不利于应用工作者选择合适的方法解决实际问题。Lv和Fan[56]建立了惩罚最小二乘方法的统一理论框架，但是更多的模型选择方法的计算复杂度及选择效果的比较还有待研究。未来应该加强对不同方法理论基础之间关联性的研究，例如Bickel等[57]对LASSO和DS方法的对比分析，Efron等[15]对LAR、LASSO及逐段向前法三者关系的研究等都提供了很好的向导。
    2）最大风险无上界问题。这一问题在实际中极易被忽略。最大风险的界定直接关系到模型选择估计参数的可靠性，在惩罚因子模型选择进一步发展之前，更多的研究应投入到这个问题上，以解决制约这一系列方法可靠性的负面效应。更多的讨论可参考Leeb与Ptscher[25-27]等。
    3）进一步打破数据维数的制约。尽管惩罚似然函数模型选择方法不像子集选择法那样受到数据维数的严重制约，但是很多方法在应用于典型的高维问题（变量个数远大于样本量）时，仍承受着维数的困扰[58]。例如，LASSO方法选择的模型所含变量个数不能超过样本量等。这些困难的全面克服需要研究者对高维问题有更深入的认识。更多的可参考Bickel等[59]，Fan和Li[1]，Greenshtein[60]，Greenshtein和Ritov[61]等。
    4）运算速度。虽然现在的方法已计算可行，但是计算成本仍然过高。以交叉验证为例，其选择调整参数的计算成本非常高，这制约着模型选择方法应用于解决实际问题。
    5）不同模型类型和不同数据类型下的模型选择。目前多数的理论研究仍集中于线性模型的选择问题。未来应将相应方法推广到非线性模型、非参数模型、半参数模型等复杂模型，特别是模型类型不同的情形，并探索其在删失数据[62]、测量误差数据[63]等方面的应用。这类研究对于实际应用有着深远的意义。
    6）最后，要真正实现这些理论方法的价值，我们需要搭建理论与实际应用的桥梁。模型选择方法应尽量做到稳健高效，所选择模型的数值和图像解释要清晰易懂，算法实现应简单可行，这样才能被不同基础的实际工作者所接受。
    参考文献：
    [1]Fan J, Li R. Statistical challenges with high dimensionality: Feature selection in knowledge discovery[A]. In: Sanz-Sole M, Soria J, Varona J L，et al, eds. Proceedings of the International Congress of Mathematicians[C]. Zurich: European Mathematical Society, 2006, 3: 595-622.
    [2]Claeskens G, Hjort N L. Model Selection and Model Averaging[M]. Cambridge University Press, 2008.
    [3]Hocking R R. The analysis and selection of variables in linear regression[J]. Biometrics, 1976, 32:1-49.
    [4]Guyon I, Elisseeff A. An introduction to variable and feature selection[J]. Journal of Machine Learning Research, 2003, 3: 1157-1182.
    [5]王大荣，张忠占.线性回归模型中变量选择方法综述[J].数理统计与管理，2010，29(4)：615-627.
    [6]Li X, Xu R. High-Dimensional Data Analysis in Cancer Research[M]. Springer, 2009.
    [7]Hesterberg T, Choi N H, Meier L, Fraley C. Least angle and penalized regression: A review[J]. Statistics Surveys, 2008, 2: 61-93.
    [8]Fan J, Lv J. A selective overview of variable selection in high dimensional feature space[J]. Statistica Sinica, 2010, 20: 101-148.
    [9]Bertin K, Lecue G. Selection of variables and dimension reduction in high-dimensional non-parametric regression[J]. Electronic Journal of Statistics, 2008, 2: 1224-1241.
    [10]Li R, Liang H. Variable selection in semiparametric regression modeling[J]. Annals of Statistics, 2008, 36: 261-286.
    [11]Tibshirani R. Regression shrinkage and selection via the lasso[J]. Journal of the Royal Statistical Society(Series B), 1996, 58: 267-288.
    [12]Breiman L. Better subset regression using the nonnegative garrote[J]. Technometrics, 1995, 37:373-384.
    [13]Yuan M, Lin Y. On the non-negative garrote estimator[J]. Journal of the Royal Statistical Society(Series B), 2007, 69: 143-161.
    [14]Fu W J. Penalized regressions: The bridge versus the lasso[J]. Journal of Computational and Graphical Statistics, 1998, 7: 397-416.
    [15]Efron B, Hastie T, Johnstone I M, Tibshirani R. Least angle regression[J]. Annals of Statistics, 2004, 32: 407-499.
    [16]Zhao P, Yu B. On model selection consistency of lasso[J]. Journal of Machine Learning Research, 2006, 7: 2541-2563.
    [17]Meinshausen N. Lasso with relaxation[J]. Computational Statistics and Data Analysis, 2007, 52: 374-393.
    [18]Zou H. The adaptive lasso and its oracle properties[J]. Journal of the American Statistical Association, 2006, 101: 1418-1429.
    [19]Tibshirani R, Saunders M, Rosset S, Zhu J, Knight K. Sparsity and smoothness via the fused lasso[J]. Journal of the Royal Statistical Society(Series B), 2005, 67:91-108.
    [20]Zou H, Hastie T. Regularization and variable selection via the Elastic Net[J]. Journal of the Royal Statistical Society(Series B), 2005, 67: 301-320.
    [21]Zou H, Zhang H H. On the adaptive elastic-net with a diverging number of parameters[J]. Annals of Statistics, 2009, 37: 1733-1751.
    [22]Yuan M, Lin Y. Model selection and estimation in regression with grouped variables[J]. Journal of the Royal Statistical Society(Series B), 2006, 68: 49-67.
    [23]Zhao P, Rocha G, Yu B. The composite absolute penalties family for grouped and hierarchical variable selection[J]. Annals of Statistics, 2009, 37: 3468-3497.
    [24]Fan J, Li R. Variable selection via nonconcave penalized likelihood and its oracle properties[J]. Journal of the American Statistical Association, 2001, 96: 1348-1360.
    [25]Leeb H, Ptscher B M. Sparse estimators and the oracle property, or the return of Hodges' estimator[J]. Journal of Econometrics, 2008a, 142:201-211.
    [26]Leeb H, Ptscher B M. Model selection and inference: Facts and fiction[J]. Econometric Theory, 2005, 21: 21-59.
    [27]Leeb H, Ptscher B M. Can one estimate the unconditional distribution of post-model-selection estimators?[J]. Econometric Theory, 2008b, 24: 338-376.
    [28]Candes E, Tao T. The Dantzig selector: Statistical estimation when p is much lager than n[J]. Annals of Statistics, 2007, 35: 2313-2351.
    [29]Meinshausen N, Rocha G, Yu B. Discussion: A tale of three cousins: LASSO, L2 boosting and Dantzig[J]. Annals of Statistics, 2007, 35: 2373-2384.
    [30]Meinshausen N, Yu B. Lasso-type recovery of sparse representations for high-dimensional data[J]. Annals of Statistics, 2008, 37: 246-270.
    [31]Massy W. Principal components regression in exploratory statistical research[J]. Journal of the American Statistical Association, 1965, 60: 234-256.
    [32]Naes T, Martens H. Principal component regression in NIR analysis: Viewpoints, background details and selection of components[J]. Journal of Chemometrics, 1988, 2: 155-167.
    [33]Wold H. Estimation of principal components and related models by iterative least squares[J]. Multivariate Analysis, 1966: 391-420.
    [34]Tobias R D. An introduction to partial least squares regression[R/OL]. Technical Report at SAS Institute, http://support.sas.com/techsup/technote/ts509.pdf, 1997.
    [35]Hoskuldsson A. PLS regression methods[J]. Journal of Chemometrics, 1988, 2:211.
    [36]Jong S. SIMPLS: An alternative approach to partial least squares regression[J]. Chemometrics and Intelligent Laboratory Systems, 1993, 18: 251.
    [37]Stone M, Brooks R. Continuum regression: Cross-validated sequentially constructed prediction embracing ordinary least squares, partial least squares and principal components regression[J]. Journal of the Royal Statistical Society(Series B), 1990, 52: 237-269.
    [38]Datta S, Le-Rademacher J, Datta S. Predicting patient survival from microarray data by accelerated failure time modeling using partial least squares and LASSO[J]. Biometrics, 2007, 63: 259-271.
    [39]Nguyen D, Rocke D. On partial least squares dimension reduction for microarray-based classification: A simulation study[J]. Computational Statistics and Data Analysis, 2004, 46: 407-425.
    [40]Nguyen D. Partial least squares dimension reduction for microarray gene expression data with a censored response[J]. Mathematical Biosciences. 2005, 193: 119-137.
    [41]Cook D, Ni L. Sufficient dimension reduction via inverse regression: A minimum discrepancy approach[J]. Journal of the American Statistical Association, 2005, 100: 410-428.
    [42]Adragni K P, Cook D. Sufficient dimension reduction and prediction in regression[J]. Philos Transact A Math Phys Eng Sci, 2009, 367: 4385-4405.
    [43]Yoo J K, Cook D. Optimal sufficient dimension reduction for the conditional mean in multivariate regression[J]. Biometrika, 2007, 94:231-242.
    [44]Li K C. Sliced inverse regression for dimension reduction[J]. Journal of the American Statistical Association, 1991, 86: 316-342.
    [45]Cook D, Forzani L. Likelihood-based sufficient dimension reduction[J]. Journal of the American Statistical Association, 2009, 104: 197-208.
    [46]Golub G H, Heath M, Wahba G. Generalized cross-validation as a method for choosing a good ridge parameter[J]. Technometics, 1979, 21: 215-223.
    [47]Li K C. Asymptotic optimality of CL and generalized cross-validation in ridge regression with application to spline smoothing[J]. Annals of Statistics, 1986, 14:1101-1112.
    [48]Hutchinson M. A stochastic estimator for the trace of the influence matrix for Laplacian smoothing splines[J]. Communications in Statistics, 1989, 18: 1059-1076.
    [49]Golub G H, VonMatt U. Generalized cross-validation for large-scale problems[J]. Journal of Computational and Graphical Statistics, 1997, 6: 1-34.
    [50]Xiang D, Wahba G. A generalized approximate cross validation for smoothing splines with non-Gaussian data[J]. Statistica Sinica, 1996, 6: 675-692.
    [51]Wu Y, Boos D D, Stefanski L A. Controlling variable selection by the addition of pseudo variables[J]. Journal of the American Statistical Association, 2007, 102: 235-243.
    [52]Luo X, Stefanski L A, Boos D D. Tuning variable selection procedures by adding noise[J]. Technometrics, 2006, 48: 165-175.
    [53]Boos D D, Stefanski L A, Wu Y. Fast FSR variable selection with applications to clinical trials[J]. Biometrics, 2009, 65: 692-700.
    [54]Chen Y. False selection rate methods in the Cox proportional hazards model[D/OL]. Ph. D Thesis in NCSU, http://gradworks.umi.com/32/33/3233025.html,2009.
    [55]Meinshausen N, Buhlmann P. Stability selection[J]. Journal of the Royal Statistical Society(Series B), 2010, 72: 1-32.
    [56]Lv J, Fan Y. A unified approach to model selection and sparse recovery using regularized least squares[J]. Annals of Statistics, 2009, 37: 3498-3528.
    [57]Bickel P J, Ritov Y, Tsybakov A B. Simultaneous analysis of LASSO and Dantzig selector[J]. Annals of Statistics, 2009, 37: 1705-1732.
    [58]Donoho D L. High-dimensional data analysis: The curses and blessings of dimensionality[R/OL]. Aide-Memoire of the lecture in AMS conference. http://www-stat.stanford.edu/donoho/Lectures/AMS2000/AMS2000.html,2000.
    [59]Bickel P. J, Ritov Y, Tsybakov A B. Hierarchical selection of variables in sparse high-dimensional regression[A]. In: Berger J O, Cai T T, Johnstone I M, eds. In Borrowing Strength: Theory Powering Applications—A Festschrift for Lawrence D. Brown[C]. IMS Collections, 2008, 6: 56-69.
    [60]Greenshtein E. Best subset selection, persistence in high-dimensional statistical learning and optimization under L1-constraint[J]. Annals of Statistics, 2006, 34: 2367-2386.
    [61]Greenshtein E, Ritov Y. Persistence in high-dimensional linear predictor selection and the virtue of overparametrization[J]. Bernoulli, 2004, 10: 971-988.
    [62]Cai J, Fan J, Li R, Zhou H. Variable selection for multivariate failure time data[J]. Biometrika, 2005, 92: 303-316.
    [63]Liang H, Li R. Variable selection for partially linear models with measurement errors[J]. Journal of the American Statistical Association, 2009, 104: 234-248.^