康璞/蒋翠侠
【内容提要】
贫困与收入分配不平等是发展经济学中两个非常重要的研究方面,关于其测度方法的研究也是层出不穷。本文在对收入分布与Lorenz曲线之间等价性论证的基础上,分别采用参数与非参数两种方案来估计收入分布函数,进而给出用于测度贫困的FGT指数与测度收入分配不平等的Gini系数的参数与非参数计算方法,并将参数与非参数两类方法进行了实证上的比较。
【关 键 词】收入分布/贫困/不平等/非参数估计
引言
早期贫困与收入分配不平等的测度主要通过测度指标来完成,常用于测度贫困的指标有:Sen指数、Thon指数、Kakwani指数、FGT指数等。用于测度收入分配不平等的指标有:Gini系数、对数收入的方差、Atkinson指数、平均对数偏差、Theil指数和变化系数等。类似于随机变量分布函数的数字特征仅是体现随机变量某个方面的变化特征一样,这些指标也仅是对收入分布某个方面的描述。近年来,不少研究开始着眼于建立新的计量方法对整个收入分布函数进行估计。
对贫困与收入分配问题的讨论依赖于对收入分布的估计,常用的估计方法有两类:一类是参数估计方法,需要对累积分布函数或概率的密度函数的具体形式做出假定,进而利用数据对未知参数进行估计得到;另一类是非参数估计方法,通常利用特定的核函数来进行核密度估计得到。在参数估计方法中,大多数文献利用回归分析方法来估计未知参数,也有一些文献利用极大化熵密度的方法来估计。一些学者,如Sala-i-Martin(
在进行贫困与收入分配问题分析时,常有两种数据类型:单元数据与分组数据,前者能够提供详尽的信息,但一般研究者难以获得连续的数据结果,不利于问题的连续分析;后者是由前者经过汇总后得到的,会有一定信息损失,但一般研究者能够从统计年鉴或统计公报中容易获得,数据具有连续性。如何利用分组数据对收入分布实施有效的估计,Sala-i-Martin(
显然,收入分布是对居民收入最为详尽的描述。类似于由一般的分布函数可以得到数字特征,在收入分布的基础上,也可以构造出用于测度贫困与收入分配不平等的指标。本文的创新性工作主要表现在:首先论证了收入分布与Lorenz曲线之间的等价性,其次分别在收入累积分布函数和Lorenz曲线基础上建立贫困与收入分配不平等测度方法,最后给出用于测度贫困的FGT指数与测度收入分配不平等的Gini系数的参数与非参数计算方法。
一、收入分布与Lorenz曲线
收入分布与Lorenz曲线是两种描述居民收入分配的不同方式,但两者之间具有内在的等价性,这里对其进行说明。
(一)收入分布
设X表示收入随机变量,其概率密度函数为f(x),则其累积分布函数

表示收入不超过x发生的概率或收入不超过x的人口占总人口的比重,以收入作为横轴。以人口累积百分比作为纵轴所得到的图形。收入累积分布函数F(x)是对居民收入水平最全面与完整的刻画,其他的信息都可以由F(x)推导或衍生出来。
(二)Lorenz曲线
Lorenz曲线也是概率分布的累积分布函数的一种图形表达方式,常用来表示收入分布,即最低收入P%的居民拥有总收入L%的财富,将人口百分比放在横轴、收入百分比放在纵轴所得到的图形。由收入分布容易得到Lorenz曲线的参数方程为:
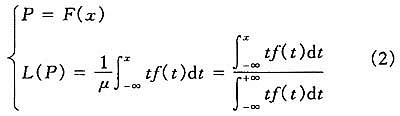
式中,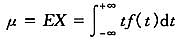
(三)两者之间联系
由式(2)可以看出,Lorenz曲线可以完全由收入累积分布函数来确定,即已知F(x),可以唯一地确定一条Lorenz曲线L(P)。反之,若已知L(P),则可以唯一地确定F(x),即Lorenz曲线也可以确定收入累积分布函数。事实上,对式(2)两端关于x求一阶导数,可得:

二、贫困与收入分配不平等测度
在Sen(1976)构建了一个全新的贫困指数之后,一系列各具特色的基于公理方法的贫困指数被开发了出来,较为著名的是由Foster、Greer和Thorbecke三位学者在1984年提出的FGT指数。过去文献中最常用Gini系数测度收入分配不平等程度,并将其总是与Lorenz曲线联系在一起。这里需要指出,由收入累积分布函数F(x)或Lorenz曲线L(P)都可以建立FGT指数对贫困进行度量、Gini系数对收入分配水平等进行度量。
(一)建立在收入累积分布函数上的贫困与收入分配不平等测度
FGT指数有离散型和连续型两种,连续形式的FGT指数可以表示为:
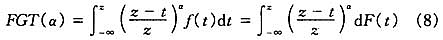
式中,z为给定的贫困线;系数α≥0用来测算不同贫困阶层对指数值的敏感性,α取值越大时,较贫困人口的收入对指数取值影响越大。FGT指数有着较强的经济含义,当α=0时,FGT(0)为贫困发生率,反映贫困的广度;当α=1时,FGT(1)为贫困缺口率,反映贫困的深度;当α=2时,FGT(2)为贫困强度率,反映贫困的强度。由式(8)可知,连续型FGT指数就是建立在收入累积分布函数F(x)之上。
一般地,Gini系数总是与Lorenz曲线L(P)联系在一起,如式(11)所示。将式(2)代入式(11),容易得到:
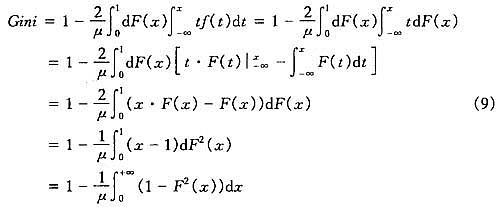
由式(9)可知,Gini系数的取值仅取决于F(x),即Gini系数也可以建立在收入累积分布函数F(x)之上。
(二)建立在Lorenz曲线上的贫困与收入分配不平等测度
林伯强(2003)给出了由Lorenz曲线L(P)表示的FGT指数:

陈奇志等(2006)在给出Lorenz曲线严格数学定义的基础上,进一步根据图1中的面积来定义Gini系数:
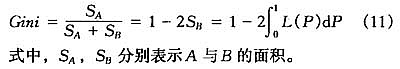
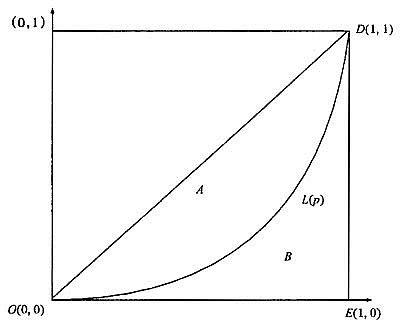
图1财富分配的Lorenz曲线
由式(10)和式(11)可知,FGT指数与Gini系数也可以建立在Lorenz曲线L(P)基础之上。事实上,还可以进一步建立贫困与收入木平等之间关系,详见林伯强(2003)的工作。
三、收入分布参数与非参数估计
对收入分布可以采用参数与非参数两种估计方案。
(一)参数估计
目前,常用于描述收入分布的参数分布主要有:Pareto分布、对数正态分布、Gamma分布、Dagum分布、广义Beta分布等,这里选用两个参数分布:对数正态分布(两个参数)与Pareto分布(两个参数)拟合收入分布。

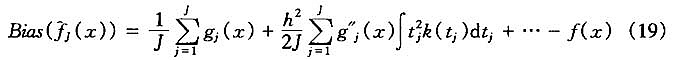
可见,基于分组数据的核密度估计的偏依赖于未知的分位数均值概率密度函数的取值。Silverman(1986)给出的基于单元数据的核密度估计的偏为:

可见,基于单元数据的核密度估计的偏依赖于未知的真实概率密度函数的取值。
四、FGT指数与Gini系数的参数与非参数估计
在收入分布的参数与非参数估计基础上,进一步给出FGT指数与Gini系数的参数与非参数估计。
(一)参数估计
Lopez等(2006)给出由对数正态分布得到的贫困指数:


五、实证研究
(一)数据选取
本文研究市场经济体制建立以来,中国城镇居民收入分布演变、收入分配及贫困变化趋势,选取中国城镇居民家庭生活情况中的收入数据作为研究对象,数据取自《中国统计年鉴》(1995~2007,有需要相关数据者可与作者联系)。年鉴中给出的是抽样调查并经过汇总后的数据,其中包括10%的最低收入户、10%的低收入户、20%的中等偏下户、20%的中等收入户、20%的中等偏上户、10%的高收入户和10%的最高收入户。显然这是一组分组数据,其实质是按照收入由低到高进行排序并按照10%、20%、40%、60%、80%、90%分位数进行分组。由该分组数据既可以直接得到分位数均值,也可以间接得到分位数的累积人口百分比与累积收入百分比,进而可以实施对收入分布的非参数及参数估计。
(二)收入分布估计
在参数估计中,由于这里使用了分组数据,故对对数正态分布与Pareto分布的参数进行估计的式(13)和式(15)应分别修正为:

图2至图4给出了三个代表性年份(1995年、2001年、2006年)的城镇居民收入分布的参数与非参数估计结果,其中左图为分位数均位处对数正态分布与Pareto分布概率密度比较,右图为收入从1000~50000之间每隔1000取一个值得到的对数正态分布与核密度估计的概率密度比较。由图2至图4的左图可知,对数正态分布与Pareto分布对数据拟合存在较大差别,特别是在低收入部分,Pareto分布的表现差强人意。由图2至图4的左图可知,对数正态分布与核密度估计对数据拟合较为一致,只是对数正态分布比核密度估计的结果要集中一些。
图5给出了三个代表性年份的城镇居民收入分布的核密度估计,可以看出随着时间的推移:①整条概率密度曲线由左向右移动,意味着城镇居民收入水平在不断提高;②概率密度曲线的顶端在下降、尾部在拉长,意味着城镇居民收入分布越来越分散;③在2001年概率密度曲线开始由单峰向双峰变化的趋势,到了2006年双峰已经较为明显,意味着收入分配呈现两极分化,其中一部分居民年收入集中在9500元左右,另一部分居民年收入集中在36000元左右。

图21995年城镇居民收入分布估计
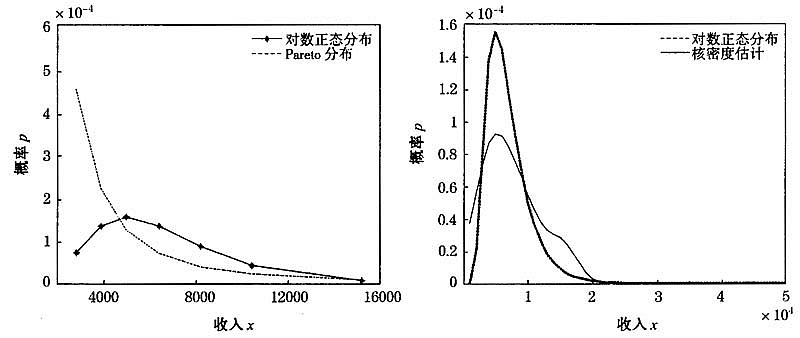
图32001年城镇居民收入分布估计

图42006年城镇居民收入分布估计
(三)贫困与收入分配不平等测度
本文选择“极端贫困线”作为国定贫困线标准,可以计算出各FGT指数(结果略),由对数正态分布与核密度估计得到的三个FGT指数都非常小,这说明国定贫困线标准偏低,难以起到有效地指导脱贫的作用。由Pareto分布估计得到的三个FGT指数出现了异常,说明利用Pareto分布拟合分组数据的收入分布有失偏颇。另外,选择1$/天的国际贫困线标准,折合人民币约为2500元/年,可以计算出各FGT指数,发现由对数正态分布与核密度估计得到三个FGT指数的估计结果较为一致,详见图6至图8。由图6至图8可以看出,总体上说,随着时间的推移三个FGT指数都不断减小,表明中国城镇居民贫困问题有所缓解。

图5城镇居民收入分布演进(基于核密度估计)

图6FGT(0)估计结果

图7FGT(1)估计结果

图8FGT(2)估计结果

图9历年Gini估计结果
图9给出了由对数正态分布、Pareto分布和非参数核密度估计的历年Gini系数,可见基于Pareto分布测度的结果失真了,而基于对数正态分布和Pareto分布测度的结果较为一致。图9表明,总体上看,Gini系数取值在逐年增加,这表明中国城镇居民收入分配不平等程度在恶化,特别是2004、2005、2006年三年基本上徘徊在0.4左右。
六、结束语
在对收入分布进行参数与非参数估计的基础上,建立了用于测度贫困的FGT指数与测度收入分配不平等的Gini系数,进而给出两个测度指标的参数与非参数估计方法。利用历年中国城镇居民收入的分组数据,分别利用参数与非参数方法进行估计,发现基于对数正态分布与核密度估计的效果优于基于Pareto分布的效果。由收入分布的动态演进可以看出,中国城镇居民收入在稳步提高,但同时收入分布呈现出两极分化的现象,与之对应,由三个FGT指数反映出中国城镇居民贫困问题有所缓解,由Gini系数反映出中国城镇居民收入分配不平等现象在恶化。
【参考文献】
[1]Schader M., Fitting parametric Lorenz curves to grouped income distribution-a critical note[J]. Empirical Economics, 1994,19:361-370.
[2]Wu X., Calculation of maximum entropy densities with application to income distribution[J]. Journal of Econometric, 2003,115:347-354.
[3]Sala-i-Martin X., The disturbing "rise" of global income inequality[R]. NBER Working Paper 8904, 2002.
[4]Sala-i-Martin X., The world distribution of income (estimated from individual country distributions)[R]. NBER Working Paper 8933, 2002.
[5]Sala-i-Martin X., The world distribution of income: falling poverty and…convergence, period[J]. The Quarterly Journal of Economics, 2006,121(2):351-397.
[6]Minoiu C. Poverty Analysis based on kernel density estimates from grouped data[R]. Working Paper, 2006.
[7]Minoiu C. Poverty Analysis based on kernel density estimates from grouped data[R]. ISERP Working Paper 07~07, 2007.
[8]Minoiu C, Reddy S G. Estimating poverty and inequality from grouped data: how well do parametric methods perform[R]. Working Paper, 2008.
[9]张建华,陈立中.总量贫困测度研究述评[J].经济学(季刊),2006年第3期.
[10]刘宗谦,曹定爱.收入分配不均等与Lorenz曲线“修补”[J].数量经济技术经济研究,2004年第8期.
[11]林伯强.中国的经济增长、贫困减少与政策选择[J].经济研究,2003年第12期.
[12]陈奇志,陈家鼎.关于洛伦兹曲线和基尼系数的一点注记[J].北京大学学报(自然科学版),2006年第5期.
[13]Dinardo J, Fortin N M, Lemieux T., Labor market institutions and the distribution of wages, 1973~1992: a semiparametric approach[J]. Econometrica, 1996,64(5):1001-1044.
[14]李竹渝.非参数统计方法对收入分布的解释[J].预测,2001年第4期.
[15]黎波,迟巍,余秋梅.一种新的收入差距研究的计量方法——基于分布函数的半参数化估计[J].数量经济技术经济研究,2007年第8期.
[16]陈昌兵.各地区居民收入基尼系数计算及其非参数计量模型分析[J].数量经济技术经济研究,2007年第1期.
[17]徐现洋,王海港.我国初次分配中的两极分化及成因[J].经济研究,2008年第2期.
[18]Silverman B W., Density estimation for statistics and data analysis[J]. Monographs on Statistics and Applied Probability, 1986, 26.
[19]Lopez J H, Servén L., A normal relationship? Poverty, growth, and inequality[R]. World Bank Policy Research Working Ppaer 3814, 2006.
[20]Schader M., Fitting parametric Lorenz curves to grouped income distribution-a critical note[J]. Empirical Economics, 1994,19:361-370.
[21]Moothathu T S K., Sampling distribution of Lorenz curve and Gini index of the Pareto distribution[J]. Sankhya, 1985,47:247-258.^
【原文出处】《数量经济技术经济研究》(京)2009年5期第120~121,157页
【作者简介】康璞,北京交通大学(北京100044);
蒋翠侠,山东工商学院(烟台264005)
