张学良
具体到长三角各省市内部,浙江省与江苏省县市区各类因素对经济增长贡献的排序与长三角132个县市区总体情况相类似,其中物质资本存量对经济增长的贡献最大,人力资本存量次之。这说明主导浙江省与江苏省经济增长的仍然是物质资本存量,物质资本的投资与积累对这两个沿海省份的贡献最大。上海的经济增长指数为5.098,这一数据高于同期的江苏与浙江两省,这表明浦东开发以来,上海的经济增长速度总体上快于江苏、浙江两省。就经济增长的源泉来看,与江苏、浙江两省市所不同的是,上海市效率改善对经济增长的贡献最大,为2.2,这直接决定了上海市全要素生产率对经济增长的贡献最大并主导着经济增长。
正如我们所知,变异系数是反映差异性的重要指标。在表1中,1993-2006年长三角县市区经济增长指数的变异系数为0.236,小于徐现祥与舒元(2004)和郝睿(2006)计算出的全国省际经济增长差异,这说明长三角县市区经济增长差距可能小于全国各省市区的差距。另外,物质资本、人力资本、效率改善与技术进步的变异系数分别为0.54、0.469、0.525与0.223,前三者较大,而后者较小,这说明长三角县市区的经济增长差异可能主要归因于物质资本、人力资本与效率改善因素。长三角县市区经济增长差异影响因素的多维性提示我们,在对长三角县市区经济增长差异进行研究时,有必要分别考虑经济增长中各个增长因素的收敛性。
三 基于要素分解的长三角地区经济增长收敛性分析
改革开放以来特别是上海浦东开发以来,长三角区域经济得到了持续快速的发展,长三角地区人均收入水平也得到了显著的提高。在长三角这样一个相对发达的区域,地区差距是在扩大还是在逐步缩小,是不是如部分学者所分析的那样会出现所谓的“俱乐部收敛”(蔡昉与都阳,2000;沈坤荣与马俊,2002;彭国华,2005),这是本文接下来想要回答的问题。我们在本部分将经济增长及其分解因素与经济收敛联系起来,分别考察人力资本、技术进步、效率改善与物质资本积累对长三角县市区经济收敛的作用。
区域经济增长可能受到空间效应的作用,即存在着地域差异和地理空间上的依赖性。也就是说一个地区的经济增长会影响其邻近地区的经济增长,不同地区的经济增长可能存在着示范效应、带动效应与模仿效应。例如,在长三角地区,距离上海较近的昆山、苏州等城市,经济增长就保持着较快的速度。张学良(2009)的研究也发现,长三角县市区在空间上呈现出明显的中心-外围模式,长三角富裕的县市区在空间上出现聚集倾向,相应地,落后的地区也会被其他落后地区所包围,而且从整体上看,长三角经济增长表现出从区域中心向南北两端递减的趋势。然而现有文献中还没有学者考虑空间依赖性对经济增长源泉即经济增长各贡献因素收敛性的影响。本文将分析长三角地区经济增长的空间依赖性,并在运用DEA方法对经济增长进行分解的基础上,建立空间计量模型来对长三角县市区经济增长及其分解指数的收敛性做进一步的分析。
(一)长三角地区经济增长的空间依赖性分析
Moran's I指数可以帮助我们更加科学地分析经济现象的空间依赖与数据的空间自相关特征。Moran's I的取值一般在-1-1之间,大致来说,大于0为正相关,表示空间空间邻接单元存在相似的属性;小于0为负相关,表示空间邻接单元不存在相似的属性;等于0表示不相关,属性值在空间上服从随机分布。表2给出了长三角县市区经济增长及各增长源泉的Moran's I指数,可以看出,各变量的Moran's I指数均显著为正,这说明长三角县市区经济增长及各增长源泉均存在显著的正的空间自相关性。
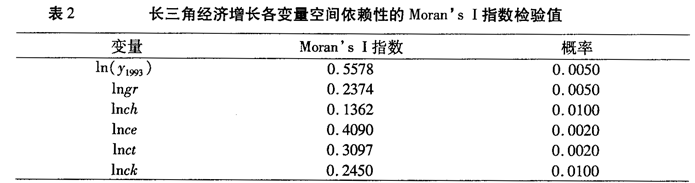
Moran散点图也可以用来分析数据的空间分布特征。Moran散点图的四个象限分别对应于空间单元与其邻近区域单元之间四种类型的局部空间联系形式:第一象限代表高观测值的空间单元为同是高值的区域所包围;第二象限代表低观测值的空间单元为高值区域所包围;第三象限代表低观测值的空间单元为同是低值的区域所包围;第四象限代表高观测值的区域单元为低值区域所包围。第一、三象限表示观测值之间存在正的空间自相关关系,而第二、四象限表示观测值之间存在负的空间自相关关系,如果观测值均匀地分布在四个象限,即表明地区之间不存在空间自相关性。图1的Moran散点图表明,大部分数据落在第一象限与第三象限,表示长三角地区经济增长各变量均呈现出正的空间相关关系。
(二)模型与结果
本文选择标准的β绝对收敛方程作为基础模型,来分析长三角县市区经济收敛性以及各因素在经济收敛中的作用。以劳均产出增长指数gr为例,建立的β绝对收敛方程如下式:
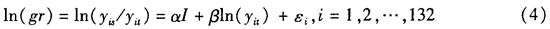
其中,yit表示第i个地区第t年的劳均真实生产总值,yis表示第s年的劳均真实生产总值。I表示单位向量,α和β是待估参数。如果(4)式中的估计系数β<0,则说明长三角县市区经济增长在t-s年是收敛的,即落后地区的经济增长速度比发达地区快,否则就说明t-s年长三角县市区的经济增长是发散的。
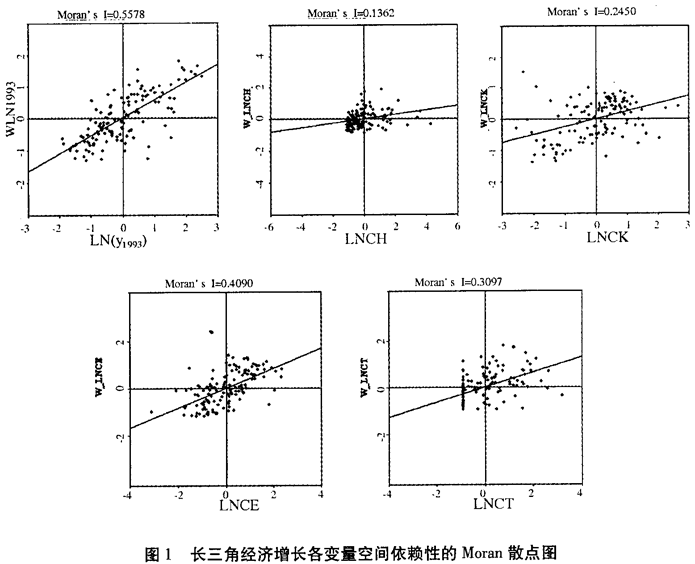
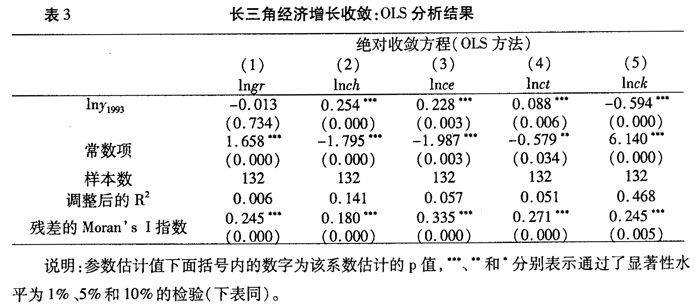
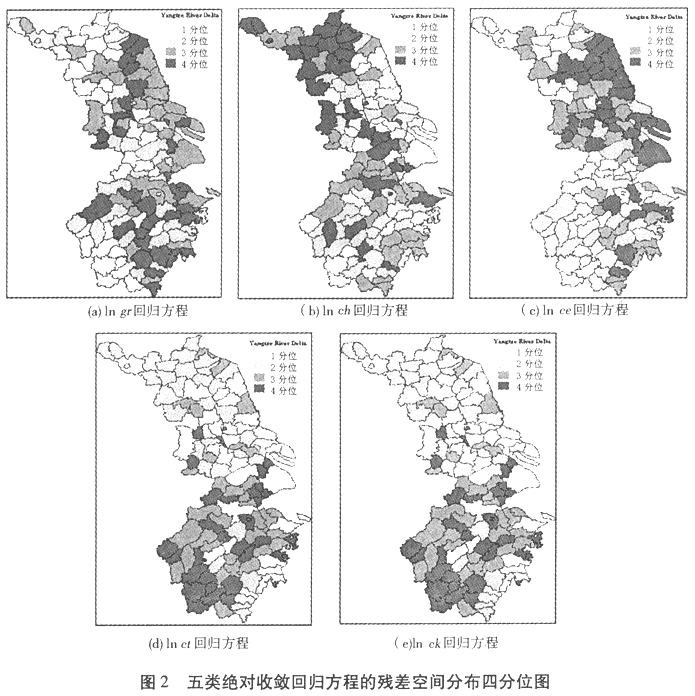
通过前面的空间自相关检验,我们发现长三角经济增长及各分解因素存在着显著的空间依赖关系,如果运用传统的普通最小二乘(OLS)法进行β绝对收敛分析,估计系数可能会是有偏的或非一致的。表3给出了运用传统OLS方法估计绝对收敛方程得到的结果,图2用空间地图的形式,较为形象地给出了表3中五类回归方程的残差项在空间上的分布。可以看出,OLS估计的回归方程残差值表现出很强的空间聚集特征。以图2(c)效率改善收敛方程的残差值为例,相对较大的正的残差值集中在江苏北部沿海一带(图中较深的颜色),而相对较小的负的残差值集中在浙江西南部一带(图中较浅的颜色),这说明表3中的效率改善收敛模型在地理空间上会系统性地高估部分地区的增长率(产生负的残差值),同时又会低估另一部分地区的增长率(产生正的残差值)。其他方程的回归方程残差值也呈现出同样的空间聚集特征。这形象地告诉我们,在没有考虑空间依赖与空间相互作用的绝对收敛方程中,计算结果可能是有偏的,在空间上表现出非随机分布的特征。表3最后一行给出的各回归方程残差值的Moran's I指数显著地大于0,这也证明了各方程残差确实存在着正的空间相关性。
来源:《世界经济》2010年第3期
责任编辑:奇奇
