会员登录
会员注册内容提要：基于包含实际总产出、货币供给M2和CPI的向量自回归模型(VAR)，将CPl分解为长期变动趋势和短期波动项。将长期趋势部分定义为核心通货膨胀率。运用1994～2009年中国季度数据进行实证检验，核心通胀率与CPI有长期均衡关系，主导CPI的长期变动趋势，是CPI的前导变量，能够为预测CPI提供有用信息，对为中央银行判断总体通货膨胀走势、制定及时有效的货币政策有所启示。
关键词：核心通货膨胀率/货币政策/向量自回归模型/共同趋势
作者简介：张延群(1968-)，女，经济学博士，中国社会科学院数量经济与技术经济研究所副研究员（北京100732）。
一、引言
1993年中国颁布了第一部中央银行法，将货币政策的最终目标确定为保持人民币币值的稳定，并以此促进经济增长。在设定货币政策的最终目标时，将居民消费价格指数CPI作为度量通货膨胀的指标。CPI是衡量居民生活成本变化的较好指标，但易于受到暂时性因素的影响，有时并不能反映总体物价水平的变动趋势。我国按照居民消费支出的比重确定各类价格指数在CPI中的权重。由于食品支出的比重较大，其价格变动会对CPI产生较大的影响。一些临时性的供给冲击，如恶劣的天气，或者农产品生产的周期性因素，会在短期内引起食品价格以及CPI的较大增长，却不能反映总体物价水平的变动趋势。例如，2007年第3、4季度CPI增长率高达6.5%，其中猪肉等肉制品价格上升了30%～45%，从而引起食品价格上涨超过16%；近几年，国际石油、原材料等大宗商品价格快速上涨也对CPI造成较大冲击，形成输入型通货膨胀。2008年上半年CPI增长率超过了8%，就是食品价格与燃料等原材料价格上涨叠加的结果。
对于这种由于暂时的供给冲击或者输入型通胀引起的结构性物价上涨，货币当局不应采取紧缩性的货币政策，否则将会对正常的经济运行产生负面影响（米什金，2008）。因此，中央银行在制定货币政策时，需要区分CPI变动中的暂时成分和永久成分，而后者在文献中常常称为核心或者趋势通货膨胀率。寻找到一种能够反映通货膨胀潜在变化趋势的、具有前瞻性的、能够对预测通货膨胀提供有用信息的核心通货膨胀的衡量指标，对于制定及时有效的货币政策意义重大。
计算核心通胀的方法的第一类方法为剔除法，即剔除价格水平会在短期内发生剧烈波动的成分，如食品和能源价格的变动，或者，更一般地，通过给各个分类施加不同的权重，重新估计出核心通胀(Wynne, 1999)。第二类方法是通过统计方法计算潜在的通胀(Bryan and Cecchetti, 1993)，如通过对CPI中的各种成分进行截尾均值和加权均值等，即将CPI中变化最高和最低10%的成分去掉，将剩余的80%作为衡量潜在通胀率的指标。第三类方法是通过时间序列计量技术如HP滤波(Hodrick-Prescottfilter)等识别出CPI中的趋势项、季度成分、以及不规则成分(Roger, 1998)。第四类方法是以经济学理论为基础，假设通胀受到两种冲击的影响，这两种冲击通过对产出的不同影响来区分。在包含产出和CPI两个变量的向量自回归(VAR)模型中，假设累积的核心通胀冲击对产出没有长期的影响，而非核心通胀冲击对产出有长期影响。将与第一类冲击伴随的通胀定义为核心通胀(Quah and Vahey, 1995)。这种方法被加以扩展并大量用于估计各国的核心通胀率(Bagliano and Morana, 2003)。
计算核心通货膨胀的方法各有特点，如以不同权重或者截尾均值方法计算的核心通货膨胀，有助于剔除供给冲击的短期影响，正确度量整体价格水平的变化，但不是反应通胀率潜在变化趋势的前导指标。因为食品和能源价格会对CPI产生强烈的暂时影响，对潜在CPI的影响是间接和滞后的，因此，以这种方法计算的潜在CPI实际上是滞后于CPI本身变化的（Marques等，2003）。运用HP滤波方法可以将CPI中的趋势性成分分解出来，但是不能反映货币政策和产出缺口对潜在通胀趋势的影响。Quah and Vahey(1995)方法被广泛应用于识别CPI中反映长期变动的趋势项，这种方法是在共同趋势模型中施加经济结构限制，只有对结构冲击施加的限制是符合经济学理论，而且与所研究数据的信息相一致时，识别出来的结构冲击才是有意义的和可以解释的(Juselius，2006)。如果VAR模型中包含更多的变量，由于存在过多随意性，施加限制会变得非常困难。
已有一些文献对中国的核心通胀率进行了分析和计算。Wu(2007)计算了剔除食品和燃料价格的核心通胀率。简泽(2005)基于Quah and Vahey(1995)的方法估计了中国核心通货膨胀率。赵昕东(2008)扩展了QuahandVahey(1995)的两变量结构向量自回归(SVAR)模型，建立了包括消费价格指数、食品价格指数与产出的三变量SVAR模型，通过对变量施加长期约束估计了中国1986～2007的核心通货膨胀。赵留彦(2006)利用新菲利普斯曲线，通过双变量非观测成分模型估计中国的季度核心通胀率与产出缺口，通过卡尔曼滤波的平滑算法将两个变量分解为趋势和周期成分，并对1998～2002年的通货紧缩进行了评价。范跃进和冯维江(2005)和龙革生等(2008)运用各种方法计算中国的核心通货膨胀率，其中包括剔除法、截尾平均法(trimmed mean)和加权中位数法(weighted median)，并且通过计算核心通胀率及其滞后值与CPI通胀率相关性的大小，对不同方法计算的核心通货膨胀率进行了比较。
以上文献对中国核心通货膨胀进行的估计，重点是对总体通货膨胀的形势进行评价。对于核心通胀率与CPI的长、短期关系，以及是否能够对预测CPI的变动提供有用信息等，大多没有做出进一步的分析。
本研究寻找到一种能够反映通货膨胀潜在变化趋势的、具有前瞻性的、能够对预测中国通货膨胀提供有用信息的核心通货膨胀的衡量指标。通过建立包括实际GDP、实际货币供给M2、以及CPI的向量自回归模型，将CPl分解为长期趋势和短期波动两个部分，将长期趋势部分定义为核心通胀率，或者称为通货膨胀的潜在变动趋势P*，运用1994Q1～2009Q4未经调整的季度数据进行实证分析，结果显示，P*能够反映CPI潜在的长期变动趋势，与CPI有长期协整关系，是CPI的Granger原因以及前导变量，能够为预测CPI的变动提供有用的信息，因此，能够为制定货币政策提供有益参考。
本文以下部分安排如下：第二部分讨论核心通胀的统计标准，第三部分是实证分析，最后为结论总结。
二、核心通胀率指标的条件
Marques等(2003)和Freeman(1998)指出作为核心通胀指标需要满足的统计条件：条件(1)要求，如果CPI通胀率π为非平稳I(1)变量，可以分解为永久性成分π*以及暂时性成分π-π*，将π*称为核心或者趋势性通胀，则π*应为I(1)变量，
三、模型及实证分析结果
（一）计量模型和方法
为了刻画总产出缺口和货币供给对通货膨胀的影响，本文建立包含实际GDP，实际货币供给M2、以及CPI的VAR模型，基于VAR模型的移动平均表达式，将CPI指数P分解为长期变动趋势部分P*和短期波动成分P-P*，将P*定义为核心通胀率，然后按照Marques等(2003)和Freeman(1998)关于核心通胀率的标准对P*的统计性质，以及是否有助于预测CPI等进行实证检验。
非限制VAR模型设定为：
（二）实证分析结果
大量研究表明，中国货币供给是影响CPI走势的重要因素之一（张延群，2009）。同时，中国通货膨胀还受到产出缺口的影响（黄益平等，2010）。在进行实证分析时，首先建立方程(1)所表示的非限制VAR模型，包含的变量为实际GDP、实际货币供给M2以及CPI。数据为1994Q1～2009Q4未经调整的季度数据。
模型中各个变量的定义为：
首先对
进行单位根检验，结果显示，它们都是含有一个单位根的I(1)过程。对非限制的VAR模型进行估计，AIC信息标准显示滞后阶数应选择2，VAR(2)模型的误差项中没有自相关、非正态性、ARCH结构等模型误设的问题。因此，以下分析在CAR(2)模型的基础上展开。①
首先进行协整关系个数的Johansen迹检验，表1显示，模型l中存在2个协整关系，或1个共同趋势项，表达式(3)中长期影响矩阵C为3×1的满秩矩阵。
表1模型1的Johansen协整关系检验
在对协整关系的个数或者共同趋势项的个数进行限制之后，估计C矩阵以及系统的移动平均表达式(3)，估计结果如下②：
P*包含了CPI中由共同趋势项构成的长期变化趋势。
按照P*的构造，P*与CPI，记做P，具有协整关系，且协整空间为(1,-1)。P*是否满足作为核心通胀率的其他条件，即P*主导CPI的走势，P*是CPI的Granger原因，以及P*能够为预测CPI提供有用信息等，需要通过数据进行检验。
图1表示P*和P的季度同比增长率，从中可以清楚地看到，P*是CPI的前导变量。建立包含P和P*的VAR(2)模型2，检验协整关系的个数，结果表明（如表2），P*和P之间确实存在协整关系，而且长期关系的系数接近于-1。将长期系数限制为-1，
(1)检验显示接受这一限制的概率为0.73。实证分析的结果与理论是一致的。
表3中的短期调整系数α显示，当出现对均衡关系的偏离时，P向着误差修正方向进行调整，而α在P*方程中的系数是不显著的，说明P*是这一长期均衡关系的弱外生变量，主导着CPI的长期变化趋势。
Granger因果检验的结果显示（如表4），△p*是△p的Granger原因，而却不是△p*的Granger原因。在滞后阶数取2、4、8时所得到的结果是一致的。
表4模型2中的Granger因果关系检验
（三）P*对于提高CPI预测精度的检验
我们建立以下三个模型，通过比较样本期外预测的平均误差RMSE(root mean square error)，来检验P*是否能够为预测P提供有用信息。这三个模型的被解释变量都为CPI的增长率
，前两个模型作为基准模型，设定如下：基准模型1用
的滞后以及工业品出厂价格指数中的能源和原材料价格指数的变化率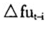
作为解释变量，基准模型2为在模型1的解释变量中加入m2的变化率，模型3是在基准模型2中的解释变量中加入误差修正项
，其中i=1,2,4，分别表示向前1、2、4步的预测。比较模型3与基准模型1和2样本期外向前1、2和4步预测的平均误差RMSE，如果模型3的RMSE小于基准模型，说明P*能够提高CPI的预测精度。所有结果通过Eviews 6编程进行计算。
运用递归分析说明结果的稳健性(robust)。递归估计的起点为1994Q3，终点从2006Q1开始，递归扩大到2009Q4，共有12个子样本。在每一个子样本中都重新计算相应的ECM项，然后放入相应的模型3中。实证结果表明，ECM在每个递归方程中都是显著的，其符号表示CPI向着误差修正的方向进行调整。图2、3、4分别表示样本期外1、2、4步预测的递归RMSE，结果表明，加入ECM项的模型3具有更好的预测效果，说明P*确实能够提高CPI的预测精度。
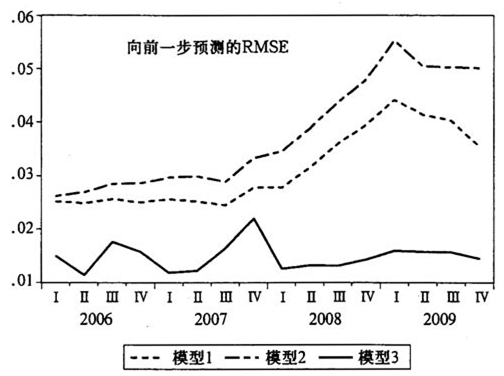
图2基准模型1、2和模型3向前1步预测的RMSE
图3基准模型1、2和模型3向前2步预测的RMSE
图4基准模型1、2和模型3向前4步预测的RMSE
（四）对CPI中短期波动部分的解释
将CPI指数中过滤掉P*后剩下的I(0)过程记作
，可以解释为CPI中的短期波动部分。为了检验
的主要影响因素，我们建立一个由方程(4)表示的辅助模型4，用燃料价格的变动△fu来解释
，其中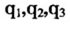
分别为季度中心哑变量。结果显示，燃料价格的波动对于解释CPI短期波动是显著的，而且及
达到0.67，如果将被解释变量换成△p*，△fu在方程中不显著，而且
非常小，为0.07，从而进一步验证了将P*作为CPI长期变动趋势的合理性。
四、结论
本文建立了包含实际产出、实际货币供给M2和CPI的VAR模型，通过对模型系统的共同趋势项进行估计，将CPI中的长期趋势与短期波动进行分离，将分离出的长期趋势P*作为核心通胀率和一种度量潜在通胀率变动趋势的指标。实证分析的结果表明，P*与CPI有长期协整关系，并且决定着CPI的长期变动趋势。它是CPI的Granger原因，而且能够对预测CPI提供有用的信息。以这种方法构造和度量的核心通胀率能够成为反映总体通货膨胀变动趋势的指标，因此可以为货币政策的制定提供参考。在后续的研究中，还可以将这种方法运用于更一般的系统，如将工资变量添加在模型中，以反映货币供给、实际产出以及劳动力成本的变动对通货膨胀趋势的影响。
注释：
①为节约篇幅，这里没有给出单位根检验和模型设定检验的详细结果，如需要，可向作者索取。
②运用Cats in Rats2.0进行计算。
参考文献：
[1]范跃进、冯维江，2005：《核心通货膨胀测量及宏观调控的有效性：对中国1995-2004的实证分析》，《管理世界》第5期。
[2]黄益平、王勋、华秀萍，2010：《中国通货膨胀的决定因素》，《金融研究》第6期。
[3]简泽，2005：《中国核心通货膨胀的估计》，《数量经济技术经济研究》第11期。
[4]龙革生、曾令华、黄山，2008：《我国核心通货膨胀的实证比较研究》，《统计研究》第3期。
[5]弗雷德里克·米什金，2008：《标题通货膨胀与核心通货膨胀》，《中国金融》第7期。
[6]赵留彦，2006：《中国核心通胀率与产出缺口经验分析》，《经济学（季刊）》第4期。
[7]赵听东，2008：《基于SVAR模型的中国核心通货膨胀的估计与应用》，《统计研究》第7期。
[8]张延群，2010：《中国货币供给分析及货币政策评价：1986～2007》，《数量经济技术经济研究》第6期。
[9]Bagliano, F. C. and C. Morana, "A common trends model of UK core inflation", Empirical Economics, vol. 28 (1).
[10]Bryan, M. F. and S. G. Cecchetti, 1993, "Measuring core inflation", NBER Working Papers 4303.
[11]Engle R. and C. W. J. Granger, 1987, "Co-integration and error correction: representation, estimation, and testing", Econometrica, vol. 55(2).
[12]Freeman, D. G., 1998, "Do core inflation measures help forecast inflation?", Economics Letters ,vok 58.
[13]Marques, C. R., P.D. Neves and L. M. Sarmento, 2003, "Evaluating core inflation indicators", Economic Modelling,vol. 20.
[14]Johansen, S., 1995, "Likelihood- Based Inference in Cointegrated Vector Autoregressive Models", Oxford University Press.
[15]Juselius, K., 2006, "The Cointegrated VAR Model: Methodology and Applications", Oxford University Press.
[16]Quah, D. and S. P. Vahey, 1995, "Measuring Core Inflation", Economic Journal, vol. 105.
[17]Roger, S., 1998, "Core Inflation: Concepts, Uses and Measurement", Reserve Bank of New Zealand Discussion Paper No. G98/9.
[18]Wu Deming, 2006, "estimating China' s core inflation rates", in "recent financial crises, analysis, challenges and implications", edited by L.R. Klein and T. Shabbir, Edward Elgar Publishing, Inc.
[19]Wynne, M. A., 1999, "Core inflation: a review of some conceptual issues", European Central Bank, Working Paperno.5.
来源：《金融研究》(京)2011年1期第64～72页