会员登录
会员注册内容提要：由于现实中的极值事件往往倾向于同时或相继发生，因此多元极值研究正成为极值统计学的理论前沿和研究热点。本文对该领域中参数建模方法的最新进展做了系统性述评，包括经典多元极值理论、Ledford-Tawn-Ramos方法和Heffernan和Tawn条件法等，并指出了这些建模方法的优缺点以及未来可能的理论突破点。本文还全面分析了近年来多元极值分析方法在金融领域的国内外应用现状，并探讨其未来的应用前景，可能是在金融传染、组合问题和系统性风险管理等方面。
关键词：多元极值 参数模型 极值统计学 极值理论 尾部相依性
作者简介：覃筱(1983-)，女，汉族，湖北松滋人，管理学博士，上海交通大学安泰经济与管理学院讲师，曾赴美国北卡罗莱纳大学统计与运筹学系和瑞士联邦理工学院伯努利研究中心访学，研究方向为金融工程、极值统计和巨灾风险；任若恩(1948-)，男，汉族，北京人，经济学博士，北京航空航天大学经济管理学院教授，博士生导师，享受政府特殊津贴，主要从事统计学和经济计量学、国民经济核算等方面的研究。
由于现实问题的复杂性，统计理论的研究都会经历由一元到多元的演变，极值统计学(extreme value statistics)这一专门刻画随机样本中异常数据的概率统计特性和规律的科学亦然①。中国成语“祸不单行”和莎士比亚名剧哈姆雷特中的名言“（坏事发生时），不会只来一件，而会来一大堆”，描述的都是现实中的极值事件越来越倾向于同时或相继发生的重要特征，例如，海岸线上的多个港口同时出现大洪水、不同股票市场同时出现暴涨或暴跌、一国多家银行先后倒闭等等。因此，构建多元极值参数模型以描述极值的相互关系，正成为该领域近年来的理论前沿和研究热点。
极值统计学最初的应用集中在自然科学和工程领域中诸如洪水、暴风雪和核爆炸的极值问题，后来又被引入体育研究领域，研究运动员的比赛记录、球类比赛的高得分等。近年来，随着宏观经济和金融、保险领域出现的巨大风险，如1997年亚洲金融危机、2005年美国“卡特里娜”飓风之后超过400亿美元的保险索赔②、2007年以来美国次贷危机所引发的全球金融危机等，经济金融领域的极端事件受到日益广泛的关注，因此，极值统计学有了新的用武之地。
本文旨在对多元极值的参数建模方法做全面述评，并探讨这些方法在金融领域的应用现状和前景，从高维度和异常金融风险的双视角对该领域的最新进展进行系统综述，这在国内外文献中并不多见。本文首先介绍一点背景知识，即极值相依性。然后介绍多元极值领域最具代表性和影响力的三类参数方法的研究进展，并深入分析这些建模方法的优缺点，依次为经典多元极值理论、Ledford-Tawn-Ramos方法和Heffernan和Tawn条件法，随后分析多元极值参数方法在金融领域的国内外应用现状，最后是总结和展望，将探讨多元极值未来可能的理论突破点及在金融领域的应用前景③。
一、相依性与极值相依性
近年来，copula方法在金融学尤其是风险管理领域研究中颇为盛行，它使用联接函数描述相依性结构，因此能够有效分离边际分布与相依性，并克服相关性存在的许多问题。copula函数的本质是随机变量为其边际分布时的多元联合分布。与相关系数相比，copula函数能够提供变量相依性更为丰富和准确的信息：已知连续的边际分布和copula，随机变量的联合分布将唯一确定；反之，已知连续的边际分布和联合分布，相依结构也唯一确定。
由于极端情况下的相依性往往更受关注，因此出现了极值相依性（或尾部相依性）以及四种渐近相依性关系④。假设随机变量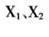
，则尾部相依性可通过极限条件概率刻画：
可见，（χ，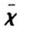
）这对指标能够完整描述随机变量之间的极值相依性或渐近关系：（χ，1）反映了渐近相依性程度；(0，
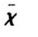)则反映了渐近独立情况下的渐近相依性。可见，尾部相依性由强至弱可分为四种：渐近相依、正关联的渐近独立、完全独立和负关联的渐近独立。图1的四个子图分别对应了这四种相依性。尾部相依性越强，则同时发生极端情况的可能性越大；从投资者的角度来看，组合中资产的尾部收益为(d)时，将最不利于风险的分散化。尾部相依性的概念将在后文中涉及。
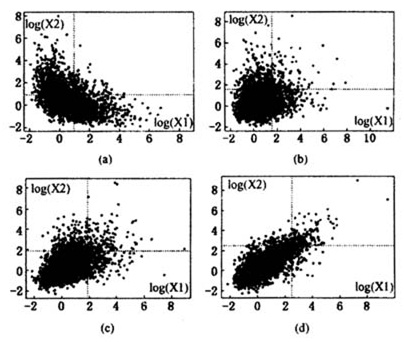
图1尾部相依性示意图
资料来源：(a)～(d)中的随机数分别来自边际分布为单位Fréchet分布，相依结构为二元正态（相关系数为-0.5）、Morgenstern copula（参数为0.75）、二元正态（相关系数为0.5）和二元极值logistic模型（参数0.5）；直线所表示的阈值为95%分位点；(a)～(d)分别对应了尾部相依性中的负关联的渐近独立、完全独立、正关联的渐近独立和渐近相依。
二、经典多元极值理论的研究
（一）由一元到多元极值理论
（二）多元极值理论下的参数模型
与一元极值理论不同，式(3)中多元情况下的极限分布G并不存在有限的参数形式，仅给出极限表示并不能有效用于统计建模、并最终研究实际问题，因此，后来的许多学者都将研究重心转移到推导合适的参数模型方面。这一问题的研究在20世纪90年代前后达到了高潮，并出现了大量颇具影响力的模型。大致可分为基于logistic分布的参数模型、基于Dirichlet分布的参数模型和其他模型三类。分别包括：logistic模型、嵌套logistic模型、负的不对称logistic模型、不对称logistic模型、双logistic模型、时间序列logistic模型；Dirichlet模型、混合Dirichlet模型；非对称混合模型等。Coles和Tawn(1991)对其中的部分模型作了综述和介绍[8]。
最近，也有学者提出了一元极值理论中的超出阈值理论所对应的多元结果，他们称之为多元广义帕累托分布(multivariate GPD)，见Rootzén和Tajvidi(2006)[9]，但研究尚初步，这里不再详述。
（三）多元极值理论及模型的优缺点
经过二十多年的发展，极值统计学者已得到了多元极值理论框架下的多个参数模型，且有二元以上的参数模型，应用范围广泛。但Ledford和Tawn(1996)指出，该理论下的相依性结构比较有限，所有参数模型所提供的相依结构仅为渐近相依或渐近独立中的完全独立中的一种，即：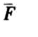
，k为常数。前者对应了极值相依结构中的渐近相依，后者对应了完全独立，但却无法描述渐近独立中的正关联和负关联。当多元变量之间是正关联关系时，例如二元随机变量的相依结构为二元正态，且相关系数略小于1，那么，此时如果使用多元极值分布对变量建模，会将二元变量视为完全独立处理，这会造成许多模型推断方面的错误，如低估两变量同时出现极端情况的可能性等等。
尽管Ledford和Tawn(1996)指出经典多元极值理论及参数模型无法给出足够丰富的相依性结构的缺陷，但是，多元极值理论下渐近独立的尾部相依性结构会消失的根源是什么？是取分量最大值的原因？是模型构造的原因？还是其他？这一问题尚未得到彻底解决。此外，在多元极值仿真方面，目前对于logistic型参数模型已有比较成熟和精确的算法，见Shi，Smith和Coles(1992)，Stephenson(2003)[10,11]，但对Dirichlet型参数模型的仿真算法却非常有限，有待进一步研究。
三、Ledford-Tawn-Ramos方法
（一）Ledford-Tawn模型框架
Ledford和Tawn(1996)基于正则变分(regular variation)理论提出了一个新的研究框架：与多元极值理论不同，他们不以分量最大值作为研究目标，转而针对联合尾部（即随机向量的各个分量均超出某个较高阈值水平的区域，如图2阴影所示）建模，考察观测值落在该区域时的统计特征，他们给出了正则变分条件下边际分布为单位Fréchet的二元随机变量的联合生存分布的一般渐进式
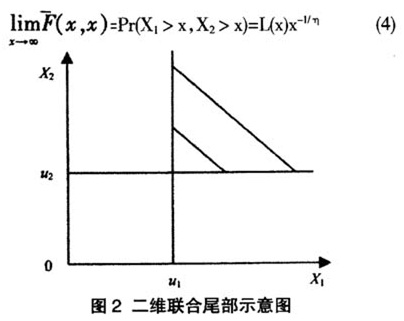
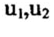为临界值。
其中，L为慢变函数，即满足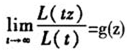
，且其极限函数g为零阶齐次函数，即g(cz)=g(z)，c＞0。0＜η≤1为尾部相依性系数(coefficient of tail dependence)，可全面反映出全部四种相依结构，η=1对应渐近相依，0＜η＜1对应渐近独立，其中η=0.5为完全独立，η＜0.5为负关联，η＞0.5为正关联。
随后，Ledford和Tawn(1997)将该模型推广到变量不对称的情况，并给出了点过程表述形式[12]。Ledford和Tawn(2003)假设时间序列具有一阶马尔可夫性，并将原模型拓展为时间序列模型[13]。近十年来，一些学者也对该模型做了进一步统计理论研究，如Coles，Heffernan和Tawn(1999)提出了针对该模型的一些新的诊断方法，Heffernan(2000)证实了Ledford-Tawn模型对于包括二元正态、二元极值logistic在内的十余种二元相依结构的普适性[14]。Peng(1999)，Beirlant和Vandewalle(2002)，Draisma等(2004)则给出了多种针对尾部相依性系数的非参数估计方法[15-17]。
（二）Ramos-Ledford的拓展及参数模型
最新的关于该模型本身的进展由Ramos和Ledford(2009)给出[18]。在对Ledford-Tawn模型进行重新表述后，类似于多元极值理论的点过程，他们给出了该模型框架下联合生存分布极限结构应满足的谱形式。
由于Ledford和Tawn模型框架中的慢变函数形式待定，因此实际运用时仍需给出满足正则条件要求的参数模型。Ledford和Tawn(1997)在提出基本模型时基于特定假设给出了一个特殊的参数模型；但Ramos和Ledford(2009)指出这个参数模型下的联合概率密度函数有时会出现负值，这显然不符合生存模型的基本要求，他们也给出了一个离散模型和一个连续模型，其中的连续模型由多元极值理论中的不对称logistic模型得出；Qin，Smith和Ren(2008)给出了构建Ledford-Tawn参数模型的一种一般性方法，并基于此方法给出了新的二元生存分布族，但三元及以上形式没有显性解，需借助数值模拟完成[19]。
（三）Ledford-Tawn-mos方法的优缺点
Ledford-Tawn模型为多元极值的理论研究提供了新思路，但也不可避免地存在着一些批评，如Schlather(2001)就认为他们的模型不能够推出极值理论中的吸引域条件，也不能由该条件推出，但未受到广泛认可[20]。此外，Ledford-Tawn-mos方法完全针对联合尾部进行建模，而这恰恰成为一些研究者对他们模型的主要批评之一，这些研究认为在变量维度足够高的情况下，能够成为研究样本的数据将非常稀缺，见Heffernan和Tawn(2004)[21]。而该方法下除联合尾部之外的数据都不在模型的考察范围内，因此原有数据的许多重要信息也许会被丢失。
但是，Ledford-Tawn模型克服了多元极值理论在刻画相依性结构方面的局限性，提供了包含丰富相依结构的理论框架，因此，自提出以来受到了极值统计领域的广泛关注和积极评价，甚至被认为是经典多元极值理论的一种较好的替代方法。因此，我们认为该模型不失为一种对联合尾部进行精确建模的好方法，尤其是在二元情况下。
需指出的是，Ledford-Tawn模型的提出不过十年，理论研究还处于发展和完善阶段。主要问题是目前满足模型要求的参数模型十分有限，仅前述的三个模型，且都是二元分布，缺乏构建满足Ledford-Tawn-mos约束的多元生存分布的一般方法。另外，Ramos和Ledford(2009)所给的参数模型没有完全解决生存分布的单调性问题，因而他们在进行统计推断时，只能通过限制搜索域进行一定的控制，但这是一种治标不治本的方法。那么，如何在多元极值参数模型的一般构建方法中，从根本理论上解决单调性问题？而且目前的Ledford-Tawn-Ramos方法基本上还是基于分布的研究，那么如何给出非平稳、自相关的时间序列下该方法对应的模型？如果这些科学问题能够得到有效解决，将极大地拓宽Ledford-Tawn模型的应用领域并改善应用效果。
四、Heffernan-Tawn的条件极值方法
（一）Heffernan-Tawn条件极值模型
Ledford-Tawn-Ramos方法只考虑所有分量同时达到极值的情况，但是维度越高，这种情形在实际中越难出现。现实问题中常有的现象是只有部分分量同时出现极值，而另一部分处于正常状态的情况，但是现有方法都无法对此进行描述。Heffernan和Tawn(2004)针对这一问题提出了多元极值的条件建模思路，假设已知多维随机向量中的某一个或某几个分量为极值，研究随机向量的条件渐近分布，并基于此提出了一种新的半参数建模方法。其基本框架为：
近年来，Heffernan-Tawn方法又陆续有了一些新的理论进展，如Heffernan和Resnick(2007)，这里不再详述[22]。
（二）Heffernan-Tawn模型的优缺点
Heffernan-Tawn方法的主要优点是针对了多元而非二元情况，由于它并不仅仅关注联合尾部，因此能够在更大程度上提取多元数据的信息。而与多元极值理论相比，该方法也能包含更多的相依性结构。另外，它可用来估计出一些实用性很强的统计量，如给定某一变量出现极值时，其余变量的条件均值、各变量之和超过某个较高水平的概率和重现水平等。
Heffernan-Tawn方法产生后，同样在多元极值统计研究领域产生了很大的影响。但是，尽管该方法的主要优点之一是它也适用于联合尾部以外的区域，我们并不能因此断言Heffernan-Tawn方法比Ledford-Tawn-Ramos方法更优越，因为它们所关注的对象不同。事实上，许多学者也对于Heffernan-Tawn方法提出了一些建议，比如，Smith(2004)就给出了一个该模型无法刻画的例子，认为他们的方法并非适用于所有情况，另外，标准化函数的形式可能也有待商榷[23]。目前条件极值方法已被证实适用于正态分布，但是对于更为广义的椭圆分布族，是否仍然有效，需要进一步的理论验证。另外，由于条件极值方法与经典的回归方法在原理上存在一定的相似性，那么如果对多元极值向量的某个分量做一元广义帕累托分布拟合，并使用其他分量作为解释变量，这种回归方法与Heffernan-Tawn的条件极值方法存在何种联系？此外，尽管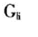
没有一般参数形式，但是否能够得出某些特殊的渐近规律。这些都是有待深入研究的问题。
经典多元极值理论、Ledford-Tawn-Ramos方法和Heffernan和Tawn方法都侧重于统计建模。近年来，Resnick教授的一系列文章给出了其更为坚实的数学背景，他们通过隐正则变分性(hidden regular variation)揭示了这些不同方法所隐含的共同特征，该特性下的几种不同条件分别对应了不同方法，见Resnick(2002)，Maulik和Resnick(2005)，Heffernan和Resnick(2005)[24-26]。
五、应用述评
（一）多元极值方法在金融中的应用
由于理论研究尚且只有短短十几年的历史，因此多元极值统计在金融领域的应用屈指可数，且集中于股票市场极值相关性的研究，因此主要是经典多元极值理论和Ledford-Tawn模型的直接应用，目前还未见Heffernan和Tawn条件法在金融领域的应用。Longin和Solnik(2001)较早地使用多元极值理论对国际五大股票市场之间的极端损失和收益做了相关性研究，后来又出现了Poon，Rockinger和Tawn(2004)，Chan-Lau，Mathieson和Yao(2004)，Hartmann，Straetmans和de Vries(2004)，Zhang和Shinki(2007)等人的研究[27-31]。但是，从目前的应用情况来看，大多数研究还是采用非参数方法估计尾部相依性系数，或是假定某种特定的相依性结构，如Longin和Solnik(2001)假定二元logistic相依结构，Poon，Rockinger和Tawn(2004)假定二元logistic和二元正态相依结构等等。因而，估计精度往往并不高，而且无法包含全面的相依性信息，因此，应用尚具有一定的局限性。
（二）国内极值统计在金融中的应用
国内已有许多学者使用了一元极值方法对金融市场收益率或保险索赔额进行了应用研究，代表性研究如，欧阳资生(2004)使用S-plus软件Finmetrics模块中的大额索赔数据，田宏伟和詹原瑞(2000)使用美元对日元汇率，封建强(2002)、柳会珍和顾岚(2006)针对股票市场时间序列极值等等[32-35]。这些文献都针对一元序列的尾部建模，计算在险价值(VaR)或条件在险价值(CVaR)，不同研究之间的主要差异在于不同金融资产的选择上，但原理都与Longin(2000)[36]类似。覃筱(2009)基于多元极值思想和方法对金融危机中的若干问题进行建模，是目前国内少见使用多元极值分析对金融极端风险的应用研究[37]。
（三）多元极值方法在金融中的应用前景述评
我们认为，多元极值研究方法未来可以在金融传染(financial contagion)、组合理论(portfolio theory)、系统性风险(systemic risk)管理等方面进行新的应用拓展：
1.金融传染方面。
目前研究金融传染的主要方法有皮尔逊相关系数、波动性溢出、协整、条件概率或probit模型、格兰杰因果等，但这些方法存在异方差、内生性、省略变量、线性、对大额和小额损失赋予相同权重等问题，因此，在度量金融传染性时可能是有偏的，见Forbes和Rigobon(2002)[38]。如果我们将一国发生的金融危机视为一元极值（但反之并不亦然），则不同区域同时爆发的金融危机可视为多元极值（反之不亦然）。事实上，考察市场的极端收益及不同市场收益的联合超量，对于金融传染性的研究可能更为恰当，也更能反映危机特征。而这正是属于多元极值中联合尾部的范畴，因此，联合尾部的研究思想就可用于对金融传染性建模。而且由于多元极值研究是非线性方法，因此，能够克服现有传染性度量方法的众多缺点。可用于解决的问题包括：一国的金融危机可能会对哪个国家或地区造成重大影响；不同国家或地区之间传染金融危机的可能性存在何种差异；等等。此外，危机研究中的双重危机可以视为同一国家不同金融体系之间的传染，例如外汇市场与银行业。因此，多元极值尤其是联合尾部的建模方法可与双重危机的理论相结合，以度量双重危机的爆发强度，进而实现不同国家外汇市场与银行业脆弱性的比较。
2.系统性风险方面。
次贷危机过后，国际社会对宏观谨慎监管的新监管模式已达成广泛共识，见美联储主席伯南克、欧洲央行行长特里谢等人近期的一系列演讲⑤。但是，对其中的核心学术问题——系统性风险的测度——尚缺乏实质而深入的研究。系统性风险的定义是，单个或若干金融个体的困境导致其他个体的级联失效乃至整个金融体系的全面崩溃⑥。其实，金融系统性风险的基本属性是尾部风险，因此，系统性风险研究应着重对尾部风险的考量，所涉及的机构困境亦可看作金融领域的一类特殊数据——极值。事实上，多元极值中的联合尾部与系统性风险的尾部风险属性极为吻合。而Heffernan和Tawn的条件极值法，针对多维随机向量中的某一个或某几个分量为极值的情况，研究随机向量的条件渐近分布，也与系统性风险的概念一致。因此，联合尾部和条件极值的统计建模方法，应该可以提供若干个新颖而有效的系统性风险测度工具，进而对宏观审慎监管提供切实可用的理论依据。可以探索的问题包括：如何识别具有系统重要性的金融机构？如何对金融系统性风险进行科学测度？金融系统与金融个体之间的风险贡献与反馈关系如何？等等。
3.组合理论方面。
组合理论由马克维茨的均值—方差框架最早确立，但真实世界中金融数据的非正态性往往使得经典的组合选择方法失效。而多元极值理论可以提供更为丰富和真实的多元尾部特征，因此，研究高阶矩下的投资组合多元化和资产配置，将是未来多元极值方法在金融领域的重要应用。多元极值分析对于尾部相依性的度量甚至可以直接为组合风险分散化提供依据：尾部相依性越大，越不利于尾部风险或系统性风险的分散；尾部相依性越小，则越有利于尾部风险分散。而Heffernan和Tawn的条件极值方法则可用于研究极端情况下的因子模型，且同时包含各个因子回报率渐近独立和渐近相依的情况。此外，投资组合风险管理中的风险度量工具，如组合VaR等的计算，通常需要对矩作出估计，但是传统方法对二阶矩及更高阶矩有较强的假设，因而对现实中呈现厚尾特征的金融回报率并不十分适用。极值分析下的特殊矩估计方法只需对一阶矩作一定假设，如L－矩及多元L－矩等，将更适于厚尾分布。因此，如果采用这些方法，可能对组合风险管理极为有效。此外，投资学中用来衡量投资业绩的Sharpe率，当存在极高回报或极低回报时，受方差的影响很大，因此基金经理往往卖出看涨期权将回报率截尾，但这种方法存在许多缺点。事实上，收益率渐近独立的资产组合尾部比渐近相依的组合尾部更瘦，因此，如果使用多元极值方法对资产进行一定的初筛，那么，不通过出售期权也能够克服Sharpe率受大额回报影响的缺陷。
此外，在保险精算领域，联合尾部方法也可以展开进一步的应用，例如，研究厚尾且相互不独立的多种保险索赔之和的尾部行为，等等。
六、总结与展望
由于现实中的复杂性，多种极值现象往往倾向于同时发生，因此对多元极值的统计研究是对现实中极值现象的更为客观和精确的刻画。本文对多元极值研究中三类典型的参数建模方法进行了系统性述评，即经典的多元极值理论、Ledford-Tawn-mos方法以及Heffernan和Tawn的条件法。
本研究表明，对多元极值的理论研究是极值统计学的必由之路和未来趋势，其研究框架和理论体系在最近十年得到了迅猛的发展，但还谈不上完美。已有的三类主要方法各具优势，又都在不同方面存在着问题或不足，但这也为该领域未来的理论研究提供了极具挑战性的课题。例如，经典的多元极值理论发展得最为成熟，且Coles和Tawn(1991)文章的出现大大丰富了多元极值理论的参数模型，但只能描述有限的相依性结构，因此方法本身存在缺陷。而Ledford和Tawn方法已提出十余年，从理论上看是针对联合尾部的一条颇为新颖的研究思路，且能够提供丰富的尾部相依性结构，但目前仍缺乏合适的参数模型，这极大限制了该方法进一步的理论拓展及实际应用。事实上，Ledford和Tawn方法面临的问题与20世纪80年代，经典多元极值理论所面临的困境非常相似，即建模框架已形成，但可用的参数模型却非常有限。另外，随着维度的增加，联合尾部的数据将越来越少，这一定程度影响了该方法向真正高维情形的拓展和应用。而Heffernan和Tawn的条件法则无法给出极值条件分布的确定参数形式。因此，未来的研究可针对这些方面进行新的理论建树。
在应用研究方面，由于宏观经济和金融保险领域出现的巨大风险，极值统计学在近二十年开始了在金融领域的应用。由于金融数据的肥尾特性决定了许多常见分布如正态分布并不适用，而极值理论能够涵盖随机变量的各种尾部特征，因此，在研究金融极端现象时引入更为科学、且完全针对尾部建模的极值方法是非常必要的。但是，目前的应用方法主要是一元极值理论，研究问题局限于在险价值的计算方面；多元极值的应用则刚刚起步，研究问题也限于股票市场极值相关性方面。因此，若能在未来拓宽应用思路、并结合现有金融理论，如金融传染、组合理论、系统性风险管理等，多元极值的参数建模方法将在金融领域具有更为广阔和良好的应用前景。
感谢国家留学基金委对第一作者赴美访问期间的资助，感谢美国北卡罗莱纳大学教堂山分校统计与运筹学系Richard Smith教授对本研究的帮助，感谢美国统计与应用数学科学研究所2007-2008年度“风险分析、极值事件和决策理论”项目及2009年瑞士联邦理工学院伯努利中心“风险、稀有事件和极值”项目参与者的有益讨论。感谢匿名审稿人和编辑对本文的修改意见。
注释：
①极大或极小的数据在统计学研究的初期是作为异常点被剔除掉的。但后来人们逐渐意识到，这些数据背后的异常事件尽管发生频率不高，但一旦发生之后，后果和影响将极为严重，因此从事概率和统计学研究的学者们开始关注并研究这些异常点，即极值，并形成了次序统计学的分支——极值统计学，这对于我们认识、管理并最终规避这些异常风险具有重要意义。
②数据来源：路透网站：http://cnreuterscom/article/usNews/idCN China-2212820080902.
③本文参考了大量学术专著和论文，如Coles(2001)第八章，Beirlant等(2004)第八、九章等[1,2].
④见Ledford和Tawn(1996)，Coles，Heffernan和Tawn(1999)[3,4]。
⑤资料来源：www.federalreserve.gov/newsevents/speech/bern anke20090310a.htm,www.ecb.int/press/key/date/2009/html/sp090324.en.html.
⑥见Wikipedia:http://en.wikipedia.org/wiki/Systemic_risk。不同于资产定价理论中的系统性风险(systematic risk)。
参考文献：
[1]Coles, S. G. An introduction to statistical modeling of extreme values[M]. London: Springer, 2001.
[2]Beirlant J., Goegebeur Y., Segers, J. et al. Statistics of extremes-theory and applications[M]. Chichester: Wiley Series in Probability and Statistics, Wiley, 2004.
[3]Ledford A. W., Tawn J. A. Statistics for near independence in multivariate extreme values[J]. Biometrika, 1996(83):169-187.
[4]Coles S. G., Heffernan J.E. Tawn J. A. Dependence measures for extreme value analyses[J]. Extremes, 1999(2):339-365.
[5]Geoffroy J. Contribution a la theorie des valeurs extremes[J]. Publ. Inst. Statist. Univ. Paris, 1958(7):37-185.
[6]de Haan L., Resnick S.I. Limit theory for multivariate sample extremes[J]. Z. Wahrscheinlichkeitstheorie verw. Gebiete, 1977(40):317-337.
[7]Pickands, J. III. Multivariate extreme value distributions (STMA V25 119)[J]. Bulletin of the International Statistical Institute, 1981(49):859-878.
[8]Coles S. G., Tawn J. A. Modelling extreme multivariate events[J]. Journal of the Royal Statistical Society, series B, 1991(53):377-392.
[9]Rootzén H., Tajvidi N. Multivariate generalized pareto distributions[J]. Bernoulli, 2006(12):917-930.
[10]Shi D., Smith R. L., Coles S. G. Joint versus marginal estimation for bivariate extremes[R]. 1992, Technical Report 2074, Department of Statistics, University of North Carolina, Chapel Hill.
[11]Stephenson A. Simulating multivariate extreme value distributions of logistic type[J]. Extremes, 2003(6):49-59.
[12]Ledford A. W., Tawn J. A. Modelling dependence within joint tail regions[J]. Journal of the Royal Statistical Society, Series B, 1997(59):475-499.
[13]Ledford A. W., Tawn J. A. Diagnostics for dependence within time series extremes[J]. Journal of the Royal Statistical Society, Series B, 2003(65):521-543.
[14]Heffernan J.E.A directory of coefficient of tail dependence[J]. Extremes, 2000(3):279-290.
[15]Peng L. Estimation of the coefficient of asymptotic independence in bivariate extremes[J]. Statistics and Probability Letters, 1999(43):399-409.
[16]Beirlant J., Vandewalle B. Some comments on the estimation of a dependence index in bivariate extreme value statistics[J]. Statistics and Probability Letters, 2002(60),265-278.
[17]Draisma G., Drees H., Ferreira A., et al. Bivariate tail estimation: Dependence in asymptotic independence[J]. Bernoulli, 2004(10):251-280.
[18]Ramos A., Ledford A. A new class of models for bivariate joint tails[J]. Journal of the Royal Statistical Society, Series B:Methodological, 2009(71):219-241.
[19]Qin X., Smith R. L., Ren R. E. Modelling multivariate extreme dependence[A], In 2008 Joint Statistical Meetings(JSM) Proceedings[C], Risk Analysis Section. Alexandria, VA: American Statistical Association. 3089-3096.
[20]Schlather M. Examples for the coefficient of tail dependence and the domain of attraction of a bivariate extreme value distribution[J]. Statistics and Probability Letters, 2001(53):325-329.
[21]Heffernan J.E., Tawn J. A. A conditional approach for multivariate extreme values[J]. Journal of the Royal Statistical Society. Series B. 2004(66):497-530.
[22]Heffernan J. E., Resnick S. I. Limit laws for random vectors with an extreme component[J]. Annals of Applied Probability, 2007(17):537-571.
[23]Smith R. L. Discussion of "A conditional approach for multivariate extreme value" by Heffernan. J. E., Tawn, J. A.[J]. Journal of the Royal Statistical Society, series B, 2004, V66:530-532.
[24]Resnick S. Hidden regular variation, second order regular variation and asymptotic independence[J]. Extremes, 2002(5):303-336.
[25]Maulik K., Resnick S. I. Characterizations and examples of hidden regular variation[J]. Extremes. 2005(7):31-67.
[26]Heffernan J. E., Resnick S. I. Hidden regular variation and the rank transform[J]. Advances in Applied Probability, 2005(37):393-414.
[27]Longin F. M., Solnik B. Extreme correlation of international equity markets[J]. The Journal of Finance, 2001(56):649-676.
[28]Poon S., Rockinger M., Tawn J. A. Extreme-value dependence in financial markets: Diagnostics, models and financial implications[J]. Review of Financial Studies, 2004(17):581-610.
[29]Chan-Lau J. A., Mathieson D. J., Yao J. Y. Extreme contagion in equity markets[J]. IMF Staff Papers, 2004(51):386-408.
[30]Hartmann P., Straetmans S., de Vries C. Asset market linkages in crisis periods[J]. The Review of Economics and Statistics, 2004(86):313-326.
[31]Zhang Z., Shinki K. Extreme co-movements and extreme impacts in high frequency data in finance[J]. Journal of Banking and Finance, 2007(31):1399-1415.
[32]欧阳资生.极值估计在金融保险中的应用[D].［博士学位论文］.北京：中国人民大学统计学院，2004.
[33]田宏伟，詹原瑞.极值理论(EVT)方法用于受险价值(VaR)计算的实证比较与分析[J].系统工程理论与实践，2000,20(10):27-35.
[34]封建强.沪、深股市收益率风险的极值VaR测度研究[J].统计研究，2002(4):34-38.
[35]柳会珍，顾岚.股票收益率波动和极值关系研究[J].统计研究，2006(10):68-71.
[36]Longin F. M. From VaR to stress testing: The extreme value approach[J]. Journal of Banking and Finance, 2000(24):1097-1130.
[37]覃筱.多元极值统计学的前沿问题及在金融危机中的应用研究[D].［博士学位论文］.北京：北京航空航天大学经济管理学院，2009.
[38]Forbes K. J., Rigobon R. No contagion, only interdependence: Measuring stock market comovements[J]. Journal of Finance, 2002(57):2223-2261.