基于全要素生产率的中国GDP数据准确性评估

内容提要：中国GDP数据的准确性评估问题，一直受到国内外各方面的关注。本文从反逻辑思路，通过考察作为技术进步的替代性指标全要素生产率(TFP)，反观GDP及其增长率是否准确或可信。运用隐性变量法通过建立状态空间模型测算中国1979-2008年间TFP增长率，分析GDP数据是否存在误差。结果表明1981年、1988年和2000年的TFP增长率的下降，找不到非正常情况下外生因素的影响，本文认为是由GDP核算误差造成的。
    关键词：GDP准确性/TFP增长率/隐性变量法
    作者简介：刘洪（1961-），男，中南财经政法大学统计与数学学院教授，博士生导师，研究方向：统计学理论与方法应用、市场调查理论与方法；昌先宇（1987-），女，中南财经政法大学统计学专业08级研究生，研究方向：统计学理论与方法应用。
    一、引言
    随着中国经济实力与国际影响力的不断增强，有关中国GDP总量及其增长速度准确性的争论亦不绝于耳。例如，我国由来已久的“省级GDP总和超过全国”现象就一直饱受诟病。2010年3月，全国政协委员王少阶在人民大会堂全体大会上作《应着力提高统计数据的公信力》的发言，“炮轰”GDP数据“打架”。2009年国际能源署(IEA)表示，中国官方公布第一季度GDP同比增长6.1%，但这一数据与中国当季石油需求下降3.5%的情况不符，与异常疲软的电力需求也不相吻合。同年5月15日《华尔街日报》根据有关国际组织报告撰写了提出对中国经济资料质疑的文章。
    由于这些质疑的声音，使得对我国统计数据准确性进行评估更显得重要。而鉴于统计数据的二手性及统计调查过程本身涉及面广，难以重复等特性，对所得统计数据的准确性进行“准确”评估存在诸多障碍，导致在研究和实践中一直未能形成评估方法的公认体系和标准。尤其是从定量角度对统计数据进行准确性评估的方法仍然在探索中，目前统计数据的评估方法主要有：逻辑性评估方法（如刘延年[10]）、误差效应分析法（如王华、金勇进[11]）、异常值检验法（如周建[16]，成邦文[2]）、相关指标建模法（如刘洪、黄燕[4-8]，刘永璋、朱胜[9]，杨海山[13]）。近年来对于经济增长的研究，很大部分采用的是全要素生产率分析法。基于此，本文从经济增长效率的角度，引入作为衡量广义技术进步的指标——全要素生产率(Total Factor Productivity, TFP)，运用我国1979-2008年间的GDP统计数据估算出该阶段的全要素生产率增长率，并依据我国全要素生产率增长的变化情况来推断我国经济增长核算是否存在误差。
    二、理论基础
    （一）全要素生产率(TFP)与GDP的相互关系
    新古典经济增长理论认为，一个经济体可以通过将更多的生产要素投入到生产过程中，或通过提升单位要素投入的效率来实现经济增长。这里的生产要素投入主要是指资本和劳动的投入，而要素的投入效率被索洛称之为“无法解释的剩余”，即广义的全要素生产率。新古典经济增长理论将经济增长的源泉分解为两项：一是各生产要素积累对总量增长的贡献；另一类是全要素生产率对总量增长的贡献。从长远来看，由于各种生产要素投入都受到边际收益递减规律的制约，而全要素生产率却具有边际收益递增的特点。所以，TFP的增长才是支持经济可持续增长的唯一源泉。（陈娟[5],2009）
    TFP的正确估算依赖于正确地计算投入、产出以及投入与产出的联系（即函数关系）三个要素。这三要素中，有两个与作为产出量指标的GDP有关。如果GDP核算是正确的，那么TFP的计算就是正确的（若方法估算得当）；反之，产出水平不真实，则无从知道真正的TFP，从而计算出来的TFP也就失去了其真正的意义。以往一般假定投入与产出水平的数据是准确的，并以此为前提计算TFP及其增长率。这是GDP核算、经济增长和TFP之间传递的正逻辑，即由GDP核算推算出经济增长，由经济增长推算出TFP。但自20世纪90年代中期以来，国内外许多学者对中国经济的持续高速增长提出质疑，认为中国的GDP核算存在准确性问题。因而产生了TFP的反逻辑，即从TFP及其增长率的角度去检验中国GDP及其增长率是否准确可信。
    这一反逻辑是否成立，依赖于技术进步的性质。最早从理论上系统研究技术进步性质的著名经济学家之一约瑟夫·熊彼特(Joseph Alois Schumpeter, 1912)，以“创新(Innovation)理论”为依据，认为经济增长和发展的真正根源在于创新或新组合，而创新需要一个时间过程或需要经历几个生产周期[11]。从本质上说，创新过程是一个累积、演进的过程，从而内生地决定了经济增长和发展的模式，即经济增长过程也必然是一个演进过程。Nathan Rosenberg(1969)认为技术进步应被视为对市场力量的压力以及信号的反应的领域。一方面必然是在出现了市场力量的压力和信号之后这种反应才出现，那么它至少要经历一个生产周期。另一方面，技术进步的扩散或模仿行为不是人们在一夜之间的共同行动，而是一个渐进的、逐步扩大的过程[7]。因此，技术进步也必然是一个相对稳定而且缓慢的演进过程。
    技术进步的这一性质表明TFP在短期内的变动必然是相对平稳的，因而为从TFP的波动形式推断GDP核算准确性提供了理论基础。换言之，在正常情况下，只要不发生外生性的历史事件，如重大自然灾害、社会动乱或天赐良机等，TFP不会在短期内发生急剧的波动，不可能出现大起大落。当TFP的增长率发生急剧波动时，应当能够找到相应的原因给予解释，例如根本性制度的变迁、外部经济环境的重大改变、大规模技术革命等等。如果在拟合的某一时间段发现TFP有超常增长或者减少的现象，却不能被上述原因所解释，一般是产出或投入测量出现了问题，则我们可以将其视为经济增长率统计的误差；这时TFP超常增长或减少的幅度即说明GDP增长率虚增或虚减的幅度。
    （二）TPP估算方法简介
    TFP的估算方法可以分为两大类：一类是增长核算方法(Growth Accounting Approach)，是延续索洛(Solow, 1957)提出的基于对总量生产函数的分解而得到的方法，后来经过丹尼森(Denison)、乔根森(Jorgenson)的拓展研究，而日趋完善。包括拉氏指数法(Laspeyres Index Approach)（也称代数指数法(Arithmetic Index Number Approach, AIN)）和索洛残差法(SR)等。它以新古典增长理论为基础，考虑因素较少而且相对简便、易于估算，但相对较为粗糙，假设约束较强，与特定国家的实际经济运行情况较难相符；另一类是经济计量方法，包括隐性变量法(Latent Variable Approach, LV)和前沿生产函数法(Frontier Production Function)（也称潜在产出法(Potential Output Approach, PO)）。它以经济计量理论为基础，建立各种模型，较为全面地考虑各种因素的影响，不需要过多的前提条件约束，可自由调整估算精细程度，但过程较为复杂。
    基于本文的目的在于通过估算TFP反观我国GDP核算数据的准确性，要与我国的实际经济运行情况相符合，因而本文主要介绍计量经济方法之一即隐性变量方法，该方法作为索洛残差法的改进，其基本思路是将TFP视为一个隐性变量即未被观测到的变量，进而借助状态空间模型(State Space Model)利用极大似然估计对TFP进行估算。该方法有两个假设前提：一是TFP、要素投入与实际产出之间存在一种函数关系；另一个是TFP遵循一阶自回归过程。为了确定TFP、要素投入与实际产出之间的函数关系，需要利用以往统计数据建立计量经济模型来估计相关的模型参数。具体估算中，为了避免伪回归，通常需要对变量数据的平稳性和协整进行检验。平稳性和协整检验的方法很多，常见的有ADF单位根检验。通常情况下产出、劳动力和资本数据的时间序列是单位根过程且三者之间不存在协整关系，并且作无量纲处理，所以往往利用这三者的一阶差分对数序列来建立回归方程。通常采用C-D生产函数，且假设规模报酬不变，建立状态空间模型[5]，则有量测方程如下：
    
    式(2)中，ρ为自回归系数且满足，|ρ|＜1,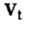  为白噪声序列。这样，利用状态空间模型，通过极大似然估计法估算出量测方程(1)和状态方程(2)。然后利用迭代算法——卡尔曼滤波(Kalman Filter)来估计状态向量的现在状态，即估计观测区间的最终时点，从而获得TFP增长的估算值。
    隐性变量方法的优点在于没有将TFP视为残差，而是将TFP视为一个独立的状态变量，从而将TFP从残差中分离出来，可以剔除掉一些影响TFP估算的测算误差。同时还避免了数据非平稳性带来的伪回归问题。
    三、实证分析
    （一）数据选取与来源说明
    由于本文是从TFP的波动形式来考察GDP总量水平与经济增长率准确性问题，研究重点是放在GDP准确性的测度方法上，故本文对投人数据的测算方法不作深入的探讨。对于相关数据尽可能采用原始数据，并且数据均来源于历年的《中国统计年鉴》。
    对于产出和劳动投入的数据，本文选用以1978年不变价的国内生产总值GDP序列作为产出的衡量指标，劳动投入以年末全国就业人数表示，即没有进行劳动力素质的修正，未考虑人力资本变动问题。
    对于资本投入数据，本文选取固定资本存量作为资本投入量的衡量指标，采用目前广泛应用的戈登史密斯(Goldsmith, 1951)开创的永续盘存法，其基本公式为：
    
    1.基年固定资本存量与固定资产折旧率的确定。
    本文采用1978年的固定资本存量作为基年固定资本存量，估计方法与Hall和Jones(1999)的相同，用基年的全社会固定资本形成总额与其后10年的全社会固定资本形成总额增长率的几何平均数与折旧率之和的比值，其公式为：
    
    式(4)中分子为以1952年为100的1978年全社会固定资本投资指数，g为1978-1988年全社会固定资本形成总额增长率的几何平均数，6为固定资产折旧率，依照Hall和Jones(1999)的方法，本文取6%[11]。构造的数据如表1：
    2.固定资产投资价格指数的构造。
    张军(Zhang，2003)指出由于价格变动的因素，特别是20世纪80年代以后，投资品的价格上升得很快，因而各年的固定资产投资价值以及固定资产原值的数据是不可比较的，所以在采用永续盘存法时，必须将当年价格表示的固定资产投资用一定的价格指数进行平减，换算成以基年不变价格表示的实际值。
    表1固定资本存量估算表

    本文借鉴张军和章元(2003)直接采用上海市的固定资产投资价格指数作为全国的相应指数估算方法，根据郭庆旺(2004)所估算的1978-2002（以1978年为基期）上海固定资产投资价格指数序列，与2003-2008年（上一年=100）的上海固定资产投资价格指数相结合，构造出完整的固定资产投资价格指数，部分数据如表1。
    3.当年投资指标的确定。
    张军等(2004)①、杨冠琼(2006)、刘洪等(2009)均认为用固定资本形成总额来衡量当年投资较为合理。本文借鉴这一结论，以全社会固定资本形成总额作为衡量指标。
    利用上述各项指标，根据式(1)和式(2)建立模型进行实证分析。
    （三）TFP的估算及GDP准确性评估
    如前文中所述，应用隐性变量方法估算中国1979-2008年TFP增长率时，须首先进行模型设定检验。具体地，本文使用平稳性检验中常用的ADF单位根检验，且对各个变量取自然对数。对于中国1978-2008年间的取对数后的实际产出序列、劳动投入序列和资本投入序列分别记为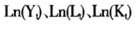经整理，ADF单位根检验结果如下：

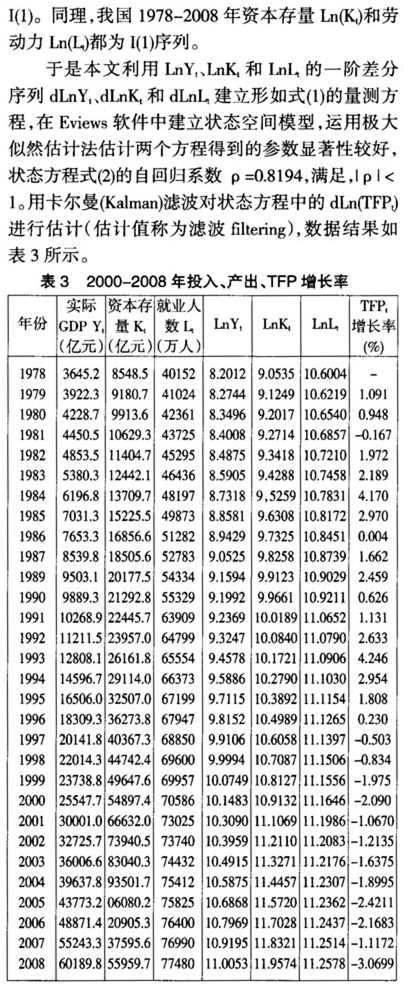
    从表3数据中可以看出，TFP增长率在1981年、1984年、1986年、1988年、1989年、1992年、1999年、2005年、2007年这9年相比前一年均有较大的波动，以1984年和1992年的两个波峰尤为明显，分别是4.17%和4.25%（最大值）；其中是负增长的有1981年、1999年、2005年、2007年、2008年，尤其是2008年的TFP增长率达到历史最低(-3.07%)，而1986年相比1985年的TFP基本没有变化。
    如前所述，在正常情况下，只要不发生外生性的历史事件，如重大自然灾害、社会动乱或天赐良机等，TFP会保持相对缓慢的变动，不可能出现大起大落。可以对TFP增长率的变化过程分为以下四个时段：
    第一个时期：1979-1988年。改革开放初期，国民经济正处于计划经济体制向市场经济体制转轨的初级时期，从1978年的农村经济改革到1984年的以城市为重点的整个经济体制改革，尤其是改革商业流通体制，极大地释放了过去被抑制的生产潜力，总产出水平的绝对量增加，劳动生产率获得提高是很自然的。因而在这个时期，我国的TFP由于受到制度因素改变的影响而呈现出强劲的增长势头。到1984年，代表着中国经济增长率的TFP增长率达到改革开放后的第一个高峰。
    第二个时期：1985-1989年。从1985年开始，国民经济开始滑落，TFP的增长也呈现下降趋势，并且在1986年TFP增长率为零，主要源于国家政治形势不稳定，改革进程缓慢，政府采取了压缩财政开支、紧缩银根的“双紧”经济政策。该经济政策的主要目的是抑制改革开放初期出现的经济过热现象。而这一阶段在1989年第二次低谷的出现，主要与西方发达国家对中国进行经济制裁有关。当时为了避免国内经济出现急剧下滑，政府增加投资支出进而拉动经济增长。而投资的过快增长势必影响到投资增长的效率，使得TFP在这个时期的增长大幅下降。
    第三个时期：1990-1994年。该时期是我国经济发展的黄金时间，1992年的新一轮经济改革，小平同志的南巡讲话，使得改革开放的范围和领域得到明显的扩大，与国际经济联系的进一步加强，全国各地采取各种措施吸引外资、先进技术、设备和生产、管理模式，从而促进了社会生产力的快速发展，推动了技术进步，直接引起生产效率的大幅度提高。因此，这个时期的TFP增长率也达到一个较高的水平，1994年TFP增长率位于4.25%的水平也不足为奇。
    第四个时期：1995-2008年。这个时期跨度较长，TFP的增速较为稳定。在1998年TFP增长率最低水平的出现，也主要是受到1997年席卷整个亚洲的金融危机的影响所致。另一方面，2006年中央下发关于促进中部地区崛起的意见，为中部地区的技术进步提供了保障，两岸经贸论坛以及中非合作论坛北京峰会等的举行都为经济注入了新活力，因而相比2005年TFP有了小幅的增长。而1007年一季度次贷危机爆发并转变成金融海啸引发了2008年的全球危机，中国的经济尤其是进出口贸易受到了强力的冲击，而2008年上半年对于中国来说更是天灾人祸，雪灾、地震接二连三，所以相比2007年，TFP的增速急速减缓自然是正常的。与2008年的天灾人祸相比，1998年的特大洪水使得1999年的经济增速相比1998年有少许放缓，这是正常现象，但应该有波动的2000年的TFP增长率却是平缓发展，如果要急速增长也应该是在2001年，这一年的成功申办奥运会以及成功加入世贸组织都给中国的经济带来不小的刺激。也就是说拐点不应该出现在1999年，而应该出现在2000年，所以本文认为2000年的GDP核算出现误差。同样，1981年、1988年的GDP的核算也出现误差。
    四、结论与评价
    本文从参数方法的计量分析角度并结合中国的实际情况，运用隐性变量方法建立状态空间模型来评估中国1978-2008年间GDP统计数据的准确性，通过全要素生产率(TFP)增长率与GDP增长率的相互关系来反观GDP数据中存在的问题，目的在于寻找更为有效地对GDP数据准确性评估的方法。
    文中运用的隐性变量法，一方面充分运用状态空间模型中的特点，将不可观测的状态变量并人可观测模型并与其一起得到估计结果[12]，将TPP视为一个独立的状态变量，从而将TPP从残差中分离出来，可以剔除掉一些影响TFP估算的测算误差；另一方面，状态空间模型中的卡尔曼滤波迭代算法在符合一定条件时，可以对模型中的所有未知参数进行估计，从而可以估计出TPP增长率的值。同时，这一评估方法，能较为有效地找出有核算误差的年份，能帮助我们更有针对性地修正GDP的核算。本文的实证分析对几个出现拐点的年份探究其原因，1984、1986年等年份都可以相应找到外生性的历史事件，如重大自然灾害、社会动乱或天赐良机等使得TPP增长率有可能出现大起大落；而1981、1988、2000年TPP增长率的骤然波动找不到合理的原因解释，从而反映GDP核算可能存在误差，即对该年份的GDP准确性提出质疑。从而印证了上述结论。
    本文是对统计数据质量评估方法的一个积极探索，但不足的是该方法的运用前提条件是投入测量要准确，目前还没有比较可行的方法，实际上对于资本投入和劳动投入的估算问题一直是学者们的讨论热点。如果资本投入和劳动投入的指标数据不准确，得到的TPP增长率则无法正确评估GDP核算的准确性。同时资本存量估算中各个变量的选取，固定资产投资价格指数的构造等，由于国家统计年鉴并没有提供1991年以前的固定资产投资价格指数，只能进行估算，也会影响到分析结果。
    注释：
    ①张军(2004)：固定资本形成总额是不包括存货的投资流量，它与经济学研究中通常所指的I具有一致的含义，同时也是和国际上通常用的固定资产投资基本一致的指标。

参考文献：

    [1]Zhang, Jun, 2003, "Investment, Investment Efficiency and Economic Growth in China", Journal of Asian Economics, 14: pp.713-734.
        [2]陈娟.全要素生产率对中国经济增长方式的实证研究[J].数理统计与管理，2009(3):277-287.
        [3]成邦文，董丽娅，杨峻.研究与开发机构统计数据质量与异常点的对数正态分布检验与识别[J].统计研究，2000(1):41-46.
        [4]郭庆旺.中国全要素生产率的估算：1979-2004[J].经济研究，2005(6):55-57.
        [5]高铁梅.计量经济分析方法与建模[M].北京市：清华大学出版社，2007:353-373.
        [6]孟连，王小鲁.对中国经济增长统计数据可信度的估计[J].经济研究，2000(10):7-9.
        [7]刘洪，黄燕.基于经典计量模型的统计数据质量评估方法[J].统计研究，2009(3):95-97.
        [8]刘洪，黄燕.我国统计数据质量的评估方法研究——趋势模拟评估法及其应用[J].统计研究，2007(8):17-18.
        [9]刘永璋，朱胜.基于VEC模型的四海上省GDP统计数据质量分析[J].经济研究导刊，2010(4):96-99.
        [10]刘延年，如何评价统计数据的质量与可靠性[J].统计研究，2002(8).
        [11]王华，金勇进.统计数据准确性评估的误差效应分析方法[J].统计与信息论坛，2009(9):10-17.
        [12]杨冠琼.中国经济增长数据可信度检验研究——理论、模型与实验证实检验[M].北京：经济管理出版社，2006:162-200.
        [13]杨海山.统计数据质量评估的组合模型[J].统计与决策，2007(7):6-8.
        [14]易纲，樊纲，李岩.关于中国经济增长与全要素生产率的理论思考[J]，经济研究，2003(8):13-15.
        [15]张军，吴桂英，张吉鹏.中国省际物质资本存量估算[J].经济研究，2004(10)，
        [16]周建.宏观经济统计数据诊断理论、方法及其应用[M].清华大学出版社，2005年.^

来源：《统计研究》(京)2011年2期第81～86页