数据误差的调整效果的评估——对杨舸和王广州商榷文章的再商榷

内容提要：本文是针对杨舸和王广州的《户内人口匹配数据的误用与改进》所提出的商榷意见的回应。基于杨文对人口普查和抽样调查数据匹配所产生的选择性偏差的讨论分析以及数据再检验结果，作者对于调整数据偏差方法及其效果进行了详细分析和数据论证，其结论是：杨文提出的商榷意见没有得到数据分析的支持，同时，杨文所采用的调整偏差的方法也不能有效地估计和解决作者相关研究的选择性偏差问题。
    关键词：人口匹配数据 选择性偏差 偏差调整
    作者简介：李春玲，中国社会科学院社会学研究所
    笔者在《社会学研究》2010年第3期上发表了《高等教育扩张与教育机会不平等——高校扩招的平等化效应考查》一文(以下简称李文)，此项研究采用了国家统计局2005年1%人口抽样调查的父子匹配数据，对大学扩招前后的高等教育不平等变化趋势做了系统考查。杨舸和王广州撰写了《户内人口匹配数据的误用与改进》一文(以下简称杨文)，对于本人所采用的数据的“选择性偏差”及其对分析结论的影响，提出了一些商榷意见，本文在此针对这些商榷意见做出回应。
    一、杨文的主要论点及其商榷意见
    杨文指出，由人口抽样调查原始数据中产生的户内人口匹配数据存在着选择性偏差，选择性偏差会影响数据分析的结果，因此需要对匹配数据进行调整处理，以减少选择性偏差，从而使数据分析结论更加可靠。杨文以李文为例，用调整处理后的匹配数据(加权数据和再抽样数据)的分析结果与李文的分析结果进行对比，期望能够发现分析结果的差异，以此证明选择性偏差对李文的研究结果产生了影响(第一个商榷)。不过，最终的数据对比发现，杨文调整后数据的分析结论与李文的结论基本一致，即杨文所提出的选择性偏差并未对李文的主要结论产生多大影响。这也就是说，杨文提出了商榷问题，但未能充分证实这一问题的存在。另外，杨文对李文的匹配数据的质量也提出了商榷(第二个商榷)：匹配程序的不同导致了匹配数据的样本数量的差异，这可能影响数据的可靠性从而也可能影响研究结论。然而，同样地，杨文也只是提出商榷问题，但未能证实这一问题，因为李文的匹配数据的相关变量的比例分布及其分析结果与杨文匹配数据基本一致。第二个商榷不是方法问题，与选择性偏差无关，它只是一个数据处理的技巧问题，因此不是本文回应的重点，而只是顺带加以说明。本文重点回应的是第一个商榷，即选择性偏差是否影响了李文的主要结论。
    二、选择性偏差对李文结论的影响有多大
    李文采用两组模型来分析高等教育机会的不平等，第一组模型是考查大学扩招前后的高等教育机会的城乡差异、阶级差异、性别差异和民族差异，第二组模型是比较大学本科与大学专科的上述差异。杨文采用了三个数据——重构数据(未调整的匹配数据)、加权数据(调整后匹配数据)和再抽样数据(调整后匹配数据)——对两组模型进行重新检验，以此评估选择性偏差对李文结论有多大影响。
    表1列出了李文数据分析结果与杨文三个数据的分析结果的比较。杨文重构数据是未调整的匹配数据，即未考虑选择性偏差的问题。杨文把重构数据与李文数据进行对比，其目的是想证明李文的匹配数据的可靠性较差(第二个商榷)，因为两个数据的样本量差距很大。①然而，表1显示两个数据得出的结论可以说相当一致。唯一明显的差异是第二组模型的“父亲月收入”回归系数，李文数据显示“父亲月收入”对大学专科机会的影响大于大学本科，而杨文数据则相反。
    
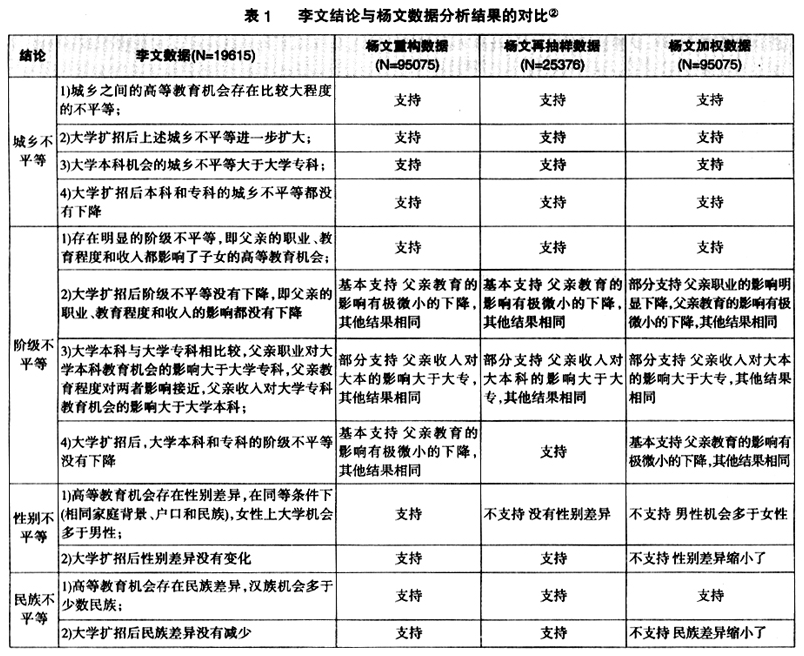
    另一处差异则几乎可以说是不算差异，李文数据显示大学扩招后父亲教育程度的影响没有变化，而杨文数据则显示其影响有所下降，但由于系数的Exp(B)接近于1(0.96)，表明其下降幅度极小。此外，杨文声称其模型的某些回归系数比李文的相应系数大一些或小一些，这应该属于正常现象。从事数据分析的研究者都知道，即使是从同样的一个总体中抽取出两个代表性相同的数据，其系数也会出现或大或小的波动。
    杨文的加权数据和再抽样数据是调整后匹配数据，即对选择性偏差进行了调整处理的数据，杨文列出这两个数据的模型再检验的目的是为了论证选择性偏差对李文结论产生了影响(第一个商榷)。杨文认为，选择性偏差最可能的影响是夸大城乡之间的高等教育机会不平等，如果这一观点得到证实，的确会对李文的研究结果构成根本性的挑战，因为李文的最主要的结论是：城乡之间存在着较大程度的不平等，而大学扩招后城乡之间的不平等进一步扩大。然而，数据对比结果显示，杨文数据分析结果完全支持李文结论，而且两者对城乡差异的估计及其扩大程度(回归系数)几乎完全一致。李文估计，城市人上大学的机会是农村人的3.4倍，而扩招后差距拉大到5.3倍；杨文再抽样数据的相应估计是3.4倍和5.2倍，杨文加权数据的相应估计是3.9倍和5.5倍。杨文提出的选择性偏差对李文分析结论可能产生的最主要影响没有得到数据证实。
    除了城乡差距的估计以外，李文的大部分结论获得了杨文加权数据和再抽样数据的支持，而且大部分的回归系数较为接近。当然，杨文的调整后数据分析结果在个别方面与李文数据有所不同，但是，无法解释的是，杨文所提供的两个调整后数据(加权数据和再抽样数据)的分析结果不一致。虽然这两个数据采用的调整策略不同——一个用加权的方式而另一个用再抽样的方式，但缩减偏差的调整原则是一致的——都是通过调整“子女的性别、户口身份、年龄、受教育程度、是否流动和婚姻”6个变量的分布比例来达到减少选择性偏差的目的，因为杨文认为匹配数据在上述6个方面存在选择性偏差并影响分析结果。从理论上来说——同时也按照杨文的推论逻辑来说，如果未调整数据因上述偏差而导致了错误结论，那么调整后数据(加权数据与再抽样数据)会因上述偏差的调整而纠正错误结论，其结果应该是这两个调整后数据与未调整数据(李文的数据和杨文重构数据)之间的差异是相同的。然而，这两个调整后数据与未调整数据的差异有明显不同。再抽样数据的分析结果与杨文的重构数据(未调整数据)的结果可以说是完全一致(除了“性别”回归系数略有变化)，也与李文数据差异极小。这也就是说，单就再抽样数据本身来看，减少选择性偏差的调整基本上未能改变原有结论，或者也可说，杨文所提出的6个方面的选择性偏差对李文数据分析结果没有明显影响。
    与再抽样数据相比较，加权数据与李文数据和杨文重构数据的差异则要多一些。其主要的差异表现在三个交互项的回归系数——“父亲职业”、“性别”和“民族”与“年龄组”的交互项，杨文的再抽样数据、重构数据和李文数据的这三个交互项的回归系数都是不显著的(即扩招后高等教育的性别差异、民族差异以及父亲职业对上大学机会的影响都没有变化)，而只有杨文加权数据的这三个回归系数是显著的(即扩招后高等教育的性别差异、民族差异以及父亲职业对上大学机会的影响有所下降)。杨文数据的这一结果的确与李文数据(同时也与杨文再抽样数据和重构数据)差异明显，这一差异是由于选择性偏差导致的吗？如果是的话，为什么再抽样数据没有得出同样的结果？杨文解释说，这是因为样本规模的原因，再抽样数据样本数量小(25376)，而加权数据样本数量大(95075)。笔者完全同意杨文的这个解释，交互项的显著水平容易受到样本数量的影响。然而，顺着这个解释我们得出的结论是，导致杨文加权数据的分析结果与李文数据分析结果的最大差别的原因，是由于样本规模不同(李文数据的样本规模与杨文再抽样数据接近)，而不是由于杨文所说的选择性偏差。样本规模大是否必然减少选择性偏差？答案是否定的，这两者之间缺乏必然联系。大样本数据的分析结论是否必然比小样本数据的结论更可靠，这也未必。样本规模增大是会减少随机误差，但会增加系统误差，哪个结论更可靠，还需要具体问题具体分析。与有关教育不平等的同类研究(采取类似分析模型的研究)相比较，李文数据和杨文再抽样数据的样本规模应该是比较大的，一般来说，不会因为样本规模而影响结论的稳定性。在实际的数据分析工作中，样本数量非常庞大可能会导致原来不显著的系数变得显著，但由此获得的结论不一定可靠，还需要参考其他数据的分析结果来判断其结论是否与现实相符。在本项研究中，李文数据、杨文重构数据和再抽样数据都显示，大学扩招后高等教育机会的阶级不平等、性别差异和民族差异没有明显减少，而仅有杨文加权数据得出的结论是上述不平等有所下降，在这种情况下，我们不能肯定地说，加权数据的结论比其他三个数据更可靠。
    杨文加权数据分析结果与李文数据(以及杨文重构数据和再抽样数据)的另一个明显差异是对高等教育机会的性别差异的估计。李文数据和杨文重构数据的结论是：在同等条件下(相同家庭背景、户口和民族)，女性上大学的可能性高于男性。杨文认为这一结论不合常理，这是由于匹配数据的性别偏误导致了这一错误结论，而加权数据纠正了这一错误，其结论是，在相同条件下，男性上大学的可能性高于女性。杨文认为加权数据的结论更符合常理，笔者对此不太认同。如果我们分析的是所有人口的高等教育机会，较为合理的结论应该是男性上大学的可能性高于女性。但是，在青年人口(本研究的分析对象)当中，男女上大学的几率较为接近，而家庭背景对女性上大学机会的影响大于男性，在控制了家庭背景及相关变量的情况下，男性上大学的可能性高于女性或低于女性并无定论，模型加入不同的控制变量会产生不同的结论。因此，并不能根据所谓的常理确定加权数据的结果更为正确。另外，李文已经指出，2005年1%人口抽样调查数据本身存在明显的性别误差(女性比例偏高)，而匹配数据又存在反方向的性别偏差(男性比例偏高)，性别偏误又与年龄和教育水平之间存在交叉偏误，如此复杂的与性别相关的误差，使这一数据不太适用于准确估计高等教育机会的性别差异。表1也显示出四个数据对性别差异的估计最为不稳定，结论各不相同，加权数据结论不仅与李文数据和杨文重构数据不同，而且也与再抽样数据不同。因此，笔者认为，杨文依此论证选择性偏差的影响不太合适。
    基于上述四种数据分析结论的对比，笔者对杨文提出的选择性偏差问题的商榷(第一个商榷)做下述几点总结性回应：第一，杨文数据支持李文数据的主要结论和大部分的结论，这说明杨文所提出的选择性偏差并未对李文结论产生明显影响；第二，杨文数据与李文数据分析结果存在的差异并非是选择性偏差导致的，而是由于其他因素导致的；第三，对于杨文数据与李文数据的结论差异，没有充分证据说明杨文的结论比李文更可靠；第四，因加权数据与李文数据分析结果差异更大而认为加权数据更可靠，杨文的这一做法不够科学严谨。另外，李文数据与杨文重构数据和再抽样数据的大部分结论相同并且回归系数相似，说明杨文提出的第二个商榷(李文数据匹配程序有误而可能导致结论错误)不成立。
    三、为什么杨文不能证实选择性偏差的影响
    杨文指出各类户内匹配数据存在选择性偏差，这些偏差可能会对数据分析结果产生影响，对此笔者十分赞同。杨文进一步提出需要对匹配数据进行调整处理以减少选择性偏差，从而纠正匹配数据的选择性偏差所导致的错误结论，对此笔者也十分认同。但是，为什么杨文的数据再检验未能证明选择性偏差对分析结论的影响，调整后数据也未能有效地改进原来数据的结论？本文认为，这可能因为杨文过于简单地理解选择性偏差的影响，其处理方式未能准确估计选择性偏差及其影响。标准的统计方法教科书对于数据偏误通常区分为两类：随机误差和系统误差。但在误差数据的调整处理的实际过程中，我们应该考虑的是另外两种误差分类。一种区分是可观测的偏差与无法观测的偏差。可观测偏差是我们可以准确估计并能够进行纠正处理的偏差，比如我们所收集的抽样调查数据通常存在年龄和性别偏差(年龄大的人和女性比例过高)，而其他信息(人口统计资料)提供了人口的实际性别比例和年龄分布，这种情况下，我们可以准确估计偏差的程度并用已获知的性别比例和年龄分布对数据进行调整处理，从而消除偏差。无法观测的偏差是我们无法准确估计并纠正处理的偏差，比如我们猜测调查数据中企业主、领导干部或流动人口的比例过低，但是我们又无法获知这些人在总人口中的实际比例，也就无法去纠正偏误。另一种误差区分是有关联的偏差与无关联的偏差。有关联偏差是会对研究结论产生影响的偏差，无关联偏差是对研究结论不会产生影响的偏差。在实际的研究工作中，我们需要考查并加以纠正的是有关联的偏差，而无关联的偏差则可以忽略。标准的定量研究的文章都会提供相关变量的描述性统计表，它提供了相关变量的比例分布或均值及标准差。研究人员通过这个统计表，对是否存在关联性偏差以及有多大程度的偏差做出基本判断，并估计这些偏差是否可能对研究结论产生影响，或者这一数据是否适用于做此类研究。
    杨文未能认真考虑上述偏差的性质区分，它只是通过匹配样本与未匹配样本的初步对比分析来估计偏差，并根据原数据(2005年1%抽样调查数据)所能提供的信息，选择“子女的性别、户口身份、年龄、受教育程度、是否流动和婚姻”这6个变量的比例调整来解决偏差问题。这6个方面的偏差是可观测的偏差，但未必都是有关联的偏差，而某些有关联的偏差可能未能包括在内。简单地对可观测误差进行调整，其效果只是改进了数据在某些方面的代表性，而未必减少了关联性偏差对研究结果的影响。同时，杨文在上述6个变量上对匹配数据进行调整还有可能产生新的关联性偏差。
    笔者在开始此项研究时，也关注了匹配数据的选择性偏差问题，而且也曾经考虑过采用与杨文类似的方式解决偏差——完全基于原始数据(2005年1%人口抽样数据)信息调整偏差，但发现这种方式在解决此项研究的偏差上有很大的局限性，可能达不到预期效果。第一个局限性是，原始数据无法提供某些重要变量的比例分布信息，从而无法估计关联性偏差的程度，比如家庭背景变量(父亲的职业、户口、教育程度和收入等)，家庭背景的样本分布会对研究结果产生极大影响，而杨文采用的方式无法解决这个问题。第二个局限是，原始数据(2005年1%人口抽样数据)本身存在某些样本偏误(如性别、年龄和教育程度)，如果我们仅根据原始数据相关信息去做调整处理，那么调整后的数据还是存在偏误的数据。杨文把原始数据作为总体的完美代表，完全基于原始数据信息进行偏差校正，这种方式不能有效地估计和校正关联性偏差。出于上述考虑，笔者采用另一种策略考查匹配数据的样本代表性和偏差程度。一是把考查的重点放在关联性偏差的评估上，即对相关变量比例分布进行细致分析，二是参考其他数据信息，以弥补原始数据缺失信息和样本偏误，从而更全面地估计关联性偏差。
    李文把匹配数据相关变量的比例分布与原始数据、中国人民大学的CGSS全国抽样调查数据、中国社会科学院社会学研究所的CGSS全国抽样调查数据进行对比，③初步判断李文数据是否存在明显的关联性偏差，是否需要对偏差进行调整，以及这个数据是否适用于这项研究。对比的结果(详细内容参见李文)显示，李文数据在相关变量的分布上较为合理，仅发现性别偏差明显，需要进行加权调整处理，因原始数据的性别比例也有偏差，李文数据是根据2000年人口普查数据的相同出生年代的人的性别比例进行加权。四种数据比较虽然不能完全否定李文数据存在关联性偏差，但可以确定的是，李文数据没有显示明显的关联性偏差，此数据可用于这项研究。
    杨文未提供其调整后数据(加权数据和再抽样数据)的相关变量的比例分布，我们无从估计杨文的数据调整(对可观测变量的调整)是否有效地减少了关联性偏差，即是否有效地减少了对研究结果可能产生影响的偏差。我们也无从判断，可观测变量的调整是否影响了相关变量的原有比例分布，而导致关联性偏差加大或产生了新的关联性偏差。杨文仅提供了重构数据(未调整的匹配数据)的相关变量比例分布，其目的是想证明杨文的匹配数据比李文的匹配数据的质量更高，因为杨文的样本数据更大和匹配程序更严谨。杨文提出两个数据的分布比例有下述几个差异。一是性别比例，这一差异应该不明显，杨文数据是65%，李文数据是63%，只不过相关变量的描述性统计表中所列的是加权后性别比例51.5%(李文对此有专门说明)。二是少数民族比例，李文数据的比例为10.1%，杨文数据为12.6%，原始数据的比例为10.4%，李文数据更具有代表性。三是接受高等教育的比例，李文数据是19%，杨文为12.1%，原始数据的比例为13.1%，社科院CGSS数据是17.8%，人大CGSS数据是27.5%(此数据的比例明显过高)，各数据比例差异较大，很难直接判断哪一个更具有代表性。不过，统计数据显示，2005年我国的大学毛入学率为21%，因此很可能李文数据比例比杨文数据更接近实际比例。另外几个差异涉及父亲职业和户口等相关比例，参考两个CGSS数据的分布情况，李文数据似乎更接近于实际分布。相关比例分布的对比，未显示出杨文数据比李文数据更具有代表性或更加可靠。
    上述分析说明，杨文仅根据原始数据信息所做的可观测偏差的调整，未能有效地解决李文的选择性偏差问题，从而不能证实李文数据是否存在关联性的选择性偏差以及这些偏差对研究结论的影响。
    四、回应总结
    杨文针对李文提出的两个商榷意见都没有得到数据分析的支持，相反，杨文的数据更有力地支持了李文的主要结论，说明杨文所提及的选择性偏差并未对李文的结论产生明显影响。同时，杨文数据与李文数据的样本分布和分析结果的对比，表明因匹配程序不同而导致的样本数量差异并未影响李文数据的代表性和可靠性。尽管杨文针对李文提出的商榷不能得到证实，但是，杨文提出的问题还是有意义的。选择性偏差不仅存在于匹配数据中而且也存在于其他类型的数据中，数据分析的研究人员需要对这一问题加以关注。杨文提出了解决选择性偏差的一种思路，这一思路的大方向是对的，虽然采用的具体方法未能对李文可能存在的选择性偏差进行有效评估，但杨文对这一问题的深入探讨是极有价值的。感谢杨文的两位作者对笔者的研究进行再检验，通过他们的再检验分析，笔者对这一问题的认识得以提高，在与他们的分析讨论中也有极大获益；笔者虚心接受两位作者对于数据匹配的技术问题的批评，在以后的研究中以更严谨的态度来改进匹配程序。两位作者对于学术研究的精益求精的态度令人钦佩。最后，笔者也欢迎学术同仁继续批评和讨论。
    注释：
    ①杨文匹配数据样本数量为95075，李文匹配数据的样本数量仅为19615。其原因是，为了简化匹配程序和减少工作量，李文仅对家庭户中排列前六位的“户主与父亲”和“户主与子女”进行配对，实际配对成功的样本数量远少于杨文；另外，在对成功配对的样本进行数据清理过程中又删除了大约1/3的样本，其中27%的样本是因缺少父亲相关信息(主要是职业和收入)而被删除，另外被删除的样本是因为个人信息相互矛盾，这样做的目的是为了提高数据信息的准确可靠。由于匹配处理程序的不同，李文最终匹配数据的样本量远远少于杨文数据。根据以往同类研究的经验，样本数在10000左右就足以进行此项研究。
    ②杨文提交给《社会学研究》编辑部的第一稿列出了重构数据、加权数据和再抽样数据的两组模型的回归系数表，本文表1是基于杨文第一稿的回归系数表归纳的数据结论，本期刊发的杨文删减了再抽样数据的回归系数表，只保留了重构数据和加权数据的回归系数表，再抽样数据的分析结果以文字方式表述。
    ③人大和社科院CGSS数据提供了家庭背景(父亲职业、教育程度、户口等)相关变量的比例分布。四种数据相关变量分布的数据表原来包括在李文的原稿中，后因《社会学研究》的版面问题把此表省略，其内容以文字方式表述。