广义线性滤波模型在非寿险准备金评估中的应用

内容提要：文章在非寿险未决赔款准备金评估中，借鉴状态空间模型如Kalman滤波在准备金评估中的应用，以广义线性模型为基础，通过在贝叶斯估计中利用泰勒展开式的二阶近似式构造了离散指数族内的后验似然函数，生成广义线性滤波，可实现动态广义线性模型的参数估计，从而能够向模型中引入新的观测数据递归出更新的参数估计结果。文章通过实例演示了伽玛广义线性滤波模型在准备金评估中的应用。
    关键词：准备金广义线性模型滤波动态广义线性模型
    作者简介：赵立戎（1985-），女，安徽淮南人，中国人民大学统计学院博士研究生，研究方向：风险管理与精算学（北京100872）。
    

0引言
    对于一个广义线性模型（GLM），按照贝叶斯统计推断的理论，假设GLM的参数向量服从某个形式已知的先验分布，其后验分布就是该参数向量关于观测数据的条件分布，通过计算参数向量的后验分布解决参数估计问题。在某些特殊情况如一元离散指数族下，能够找到自然共轭的先验分布，因而容易计算出后验分布的具体形式，此结论在多元离散指数族中并不成立。因此在一般情况下，贝叶斯GLM的后验分布形式很难直接计算，因而产生了很多近似计算的方法。例如West et al.在保留自然参数服从自然共轭先验分布的约束条件下给出了几种参数变换的形式。Fahrmeir和Kaufman研究了估计后验分布的模。近年来还有不少利用MCMC方法处理贝叶斯GLM问题的文献。在精算领域的应用如Scollnik及de Alba等人的研究。MCMC方法便于操作，但得不出后验分布的具体形式。在实际应用中，近似的解析法虽然精度高但计算过于复杂，而随机模拟方法虽然便于实现却又得不到分布形式。
    Greg Taylor[4]利用泰勒展开式，在多元离散指数族下构造出后验分布的二阶近似解析表达式，使其满足与贝叶斯GLM的先验分布同分布族的性质，并能够进一步产生迭代公式，生成一个与Kalman滤波算法类似的GLM滤波算法，可推广至动态广义线性模型（DGLM）的参数估计。这种利用二阶近似的GLM滤波算法不同于复杂的传统解析处理方法，通过使用典则联结或伴随典则联结函数能够简化计算过程。
    在非寿险准备金评估中，通常使用的确定性模型或随机性模型都假设一个不随时间变化的参数向量，它们都属于静态模型。当保险公司内部或外部环境随时间发生变化时，如果考虑模型参数及参数结构随时间发生变化，就可以使用动态模型，如精算中常用的Kalman滤波模型，张连增[6]研究了Kalman滤波法在非寿险未决赔款准备金评估中的应用。Kalman滤波模型的应用局限性在于假设观测数据服从正态分布，不能处理其他常用分布（如泊松分布、伽玛分布等）类型的数据。
    本文将从动态模型的角度出发，探讨非寿险未决准备金评估问题：应用广义线性滤波模型，基于离散指数族分布，建立关于赔付数据的动态广义线性模型；通过对流量三角形数据逐期（事故年或日历年）迭代，实现模型的参数估计和准备金评估。
    1广义线性滤波模型
    1.1贝叶斯GLM的二阶近似法
    
    
    对于势方差函数，有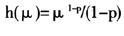，不满足对任意p∈（-∞，+∞）成立，因而可能使得b（Xβ）在某些值上没有定义。考虑到典则联结函数存在的这种问题，Taylor[4]定义伴随典则联结函数，并且在伴随典则联结函数下得到了与使用典则联结函数时一致的似然函数递推关系，仅其中涉及参数的形式发生一定的变化。常用的分布及伴随典则联结函数有伽玛分布和对数联结函数等。
    1.2动态广义线性模型
    考虑参数向量β随时间随机变化，则GLM模型形式变为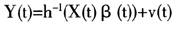：，其中Y（t）是Y在t时刻的观测数据向量，设计矩阵X（t）、参数向量β（t）和误差向量v（t）都表示t时刻的相应状态。类似状态空间模型的定义，上式为观测方程，还需定义参数演化的状态方程：β（t+1）=Φ（t+1）β（t）+r（t+1），其中Φ（t+1）为已知矩阵，r（t+1）是均值为0的随机干扰项，且与y（1），…，y（t）及β（0），…，β（t）相互独立，记Var[r（t+1）]=R（t+1）。允许参数向量的维度随时间变化。这样就构成了动态广义线性模型（DGLM）的基本形式。在实际应用中，t可以选为事故发生年，也可以选为日历年。
    利用贝叶斯二阶近似法得到的先验似然与后验似然之间的递推关系，可以在保留分布形式的同时通过不断变换参数实现多次贝叶斯GLM的模型估计。这就形成了一个与Kalman滤波类似的贝叶斯GLM序列，可以称之为贝叶斯GLM滤波或广义线性滤波，利用这一滤波算法实现对DGLM各时刻的参数估计。
    类似状态空间模型的定义，用记号t|t-j表示在t时刻利用t-j时刻之前（包t-j含时刻）的全部信息所进行的估计。使用典则联结函数时，似然函数的形式转变为：
    
    
    
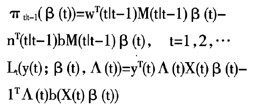
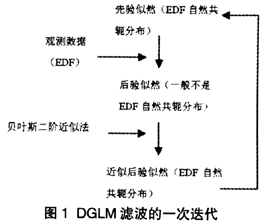
    Taylor[4]将Kalman滤波算法从动态一般线性模型推广到DGLM，保留了模型的线性系统成分。应注意的是，当使用正态分布和单位联结函数时，广义线性滤波就等于Kalman滤波，可见Kalman滤波是广义线性滤波的一种特殊情况。广义线性滤波模型的一般形式及其实现过程仍是比较复杂的，但对于几种特殊分布（如正态分布、泊松分布、伽玛分布）以及使用典则联结或伴随典则联结函数的情况，滤波迭代公式能够大为简化，因此在解决非寿险准备金评估问题时具有实际应用价值。广义线性滤波模型对各期参数的估计是基于迭代的过程，因此各期参数估计值比一般GLM的参数估计值较平滑。能够降低经验数据中的异常值对准备金估计结果的影响。在早期赔付数据缺失或观测数据出现异常值的情况下，应用广义线性滤波模型能够改善未决赔款准备金的估计结果。
    2伽玛广义线性滤波模型
    
    伽玛广义线性滤波迭代计算的具体步骤如下：
    
    
    3实例分析
    为了更好地验证广义线性滤波模型的估计效果，下面引用Taylor和Ashe（1983）[2]的数据（表1）对滤波迭代模型进行实证分析。
    
    
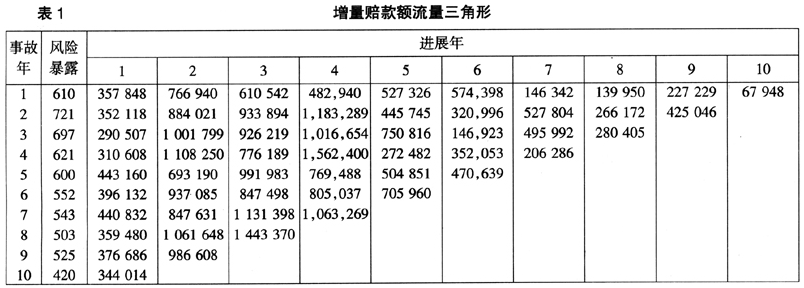
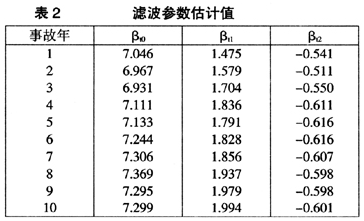
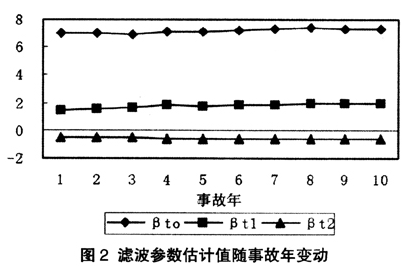
    本例中β（t）t=1，…，10参数结构未发生变化，则Φ（t）为单位阵。迭代初始值E[β（0|0]和Var[β（0|0）]选用伽玛GLM的参数估计结果。参数向量β的滤波估计值E[β（t|t）如下页表2所示。由下页图2可见由于滤波模型的估计参数之间存在递推关系，各事故年的参数估计值比较平稳，反映了增益矩阵K（t）的平滑作用，降低了观测数据中异常值的影响。
    
    
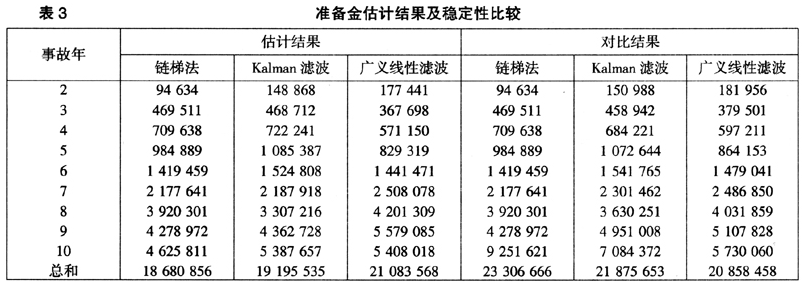
    协方差阵Var[β（t|t）的滤波估计结果选取了其中4期的结果作为示例：
    
    
    
    
    

    

    

参考文献：
    

    [1]De Jong, P. B. Zehneirth. Claims Reserving State Space Models and the Kalman Filter[J]. Journal of the Institute of Actuaries, 983,(110).
    [2]Taylor, G. Ashe, F. Second Moments of Estimates of Outstanding Claims[J]. Journal of Economics, 1983,(23).
    [3]Taylor, G. Loss Reserving: An Actuarial Perspective[M].Boston: Kluwer Academic, 2000.
    [4]Taylor, G. Second-order Bayesian Revision of a Generalized Linear Model[J]. Scandinavian Actuarial Journal, 2008,(4).
    [5]T aylor, G. Gráinne McGuire, Adaptive Reserving Using Bayesian Revision for the Exponential Dispersion Family[J]. Variance, 2009,(3).
    [6]张连增.未决赔款准备金评估的随机性模型与方法[M].北京：中国金融出版社，2008.

 

                                                                                                                                                                          责任编辑：夏雨