内容提要:针对金融收益胖尾分布特征及条件波动率长记忆性特征,运用FIGARCH对条件波动率建模、极值理论(extreme value theory,EVT)对标准收益序列的尾部建模,测度出金融市场动态极值风险,进而运用返回测试(back-testing)技术,对模型在样本内的测度准确性与样本外的推广能力进行稳健性检验.实证研究结果表明,无论是中国新兴市场,还是西方成熟发达市场,金融收益与标准收益均呈现出明显的有偏胖尾分布特征;金融收益条件波动率均展现出长记忆性特征;EVT与FIGARCH模型相结合的动态极值风险测度模型不仅在样本内表现出优越的风险测度能力,而且在样本外同样具有可靠的预测推广能力。
关键词:胖尾分布长记忆性极值理论稳健性检验
作者简介:林宇(1973-),男,四川仪陇人,博士,成都理工大学商学院副教授(成都610059),西南交通大学经济管理学院(成都610031),Email:linyuphd@126.com;黄登仕,西南交通大学经济管理学院;魏字,西南交通大学经济管理学院。
0引言
金融市场风险管理一直是政府管理当局、投资主体关注的焦点与难点。尤其是近20年来爆发了一系列全球性金融经济风险危机灾难事件,如1997年发生的亚洲金融危机,2008年出现的全球性经济危机以及最近发生的迪拜危机事件等。这些全球性重大金融风险危机事件进一步警示我们:只有强化金融市场风险管理,才能有效地维护经济安全,促进经济发展与繁荣。
在金融风险管理中最为关键的工作之一就在于准确有效地测度风险。只有准确有效地测度出金融风险,才可能保证风险管理效果,维护资本市场的稳定与发展;如果风险测度就出现偏差,那么其后所进行的风险管理活动都可能失败,自然也就谈不上风险的管理与控制。
长期以来,金融风险管理都是以有效市场假说(efficient market hypothesis,EMH)为基石的金融理论展开的,它假设金融收益服从正态/高斯分布(normal distribution/Gauss distribution),然后根据收益的分布特征来测度金融市场的风险值(value at risk,VaR)[1-2]。需要说明的是,VaR指标仍然是目前金融市场风险管理实务所采用的最为常见的方法之一,国际清算银行(the bank of international settlements,BIS)要求各大金融机构按照市场风险指标(即VaR)来安排资本充足率;许多国际金融投资机构也根据VaR方法来预测金融市场风险,并以此作出金融资产投资决策制定[3-4]。
然而,同样需要指出的是,尽管传统的VaR指标方法在测度金融市场风险上目前仍然得到了相关机构的认可与使用。但令人遗憾的是,由于近20年来计算机科学与信息技术的迅猛发展,产生了大量既不能为EMH所解释,又普遍存在于不同类型与不同地区市场当中的实证成果,如金融资产收益呈现出分布条件/非条件胖尾特征(conditional/unconditional fat tailed distribution)、金融资产价格波动的长记忆性(long memory)等重要的典型事实(stylized facts)特征,从而使传统的风险(VaR)测度方法暴露出种种缺陷[5]。也正是由于不断涌现出来的典型事实,使得金融收益并非是服从EMH条件下的正态分布或学生t分布等单一确定的分布特征,很可能是一个多分布的复合形式,而有效风险测度的关键又在于风险模型能对金融时间序列分布形态等特征有一个准确可靠的描述。因此,如果仍然按照传统的单一分布,又尤其是以正态分布来测度金融市场风险,就会大大降低风险测度的准确性,导致风险管理失效,于金融市场安全与投资者不利[6-7]。
对金融市场管理当局与投资者来说,尤其关注发生概率小、一旦发生就会带来巨大损失甚至是遭受灭顶之灾的极值事件风险,因为这类风险很可能导致投资者破产,甚至可能引发经济崩溃、社会动荡[2]。就金融收益分布而言,其尾部就代表着这一类风险,从而要求风险管理应根据金融收益的复杂分布的尾部分布进行建模分析。而极值理论(extreme value theory,EVT)就不必预先假设整个样本所服从的分布,只对分布尾部进行建模[4]。因此,应用EVT于金融风险管理研究与实务中来测度VaR,能有效克服传统风险管理的单一分布假设的缺陷,使风险测度更加准确和容易,从而受到实务界与学术界的欢迎[8-12]。
另外,金融市场涌现出大量的典型事实就要求必须以这些典型事实为约束条件来开展风险测度研究工作。一些学者运用GARCH簇模型以及随机波动(stochastic volatility,SV)模型与EVT结合对风险测度进行建模分析,虽然都取得了较好的研究效果[13-14],但由于GARCH模型无法捕获条件波动率的长记忆特征,而Bailie等人1996年提出了刻画金融收益波动率长记忆性的分数积分GARCH模型(fractional integrated GARCH,FIGARCH)[15]。由于FIGARCH能够较好刻画条件波动率的长记忆性特征,从而出现了以FIGARCH模型为基础展开的实证研究[16-18]。同时值得一提的是,目前已有学者开始运用FIGARCH模型与正态分布、学生t分布(student-t distribution)以及有偏学生t分布(skew student-t distribution,SKST)[19]相结合,对诸如中国股市这样的新兴资本市场的风险测度进行了实证研究[20-24],为以波动率长记忆性与收益率的胖尾分布为约束条件,开展中国金融市场动态风险的测度研究与实务奠定了基础。
就中国金融市场而言,成立时间短,从第一支股票上市到现在也只不过20年时间,虽然发展迅猛,目前已成为全球最大的新兴金融市场(emerging finance markets)之一,但与发达成熟的西方金融市场相比,无论是在市场监督管理等体制建设上,还是在投资者心理行为等方面都还表现出诸多的不成熟性。比如说,过剩的流动性、庄家操控以及过度的市场投机等导致市场大起大落时有发生,从而使中国金融市场经受着更多更大的风险考验,政府金融经济管理当局、投资者在风险管理方面承受着更多新的挑战[24-25]。
如上所述,金融市场呈现出收益率有偏胖尾分布与条件波动率长记忆性等诸多典型事实特征,不仅使传统的金融市场风险管理方法面临挑战,对新兴的中国金融市场有着更多的风险考验。那么,如何基于EVT与FIGARCH构建出适合金融市场实际的风险测度方法?并且构建的风险测度模型是否又能准确测度中国金融市场的动态极值风险?如果能,那么在测度西方成熟发达金融市场与中国新兴市场的风险在可靠性与精度方面是否又存在明显的差异呢?
基于以上分析与认识,以中国大陆新兴股票市场与成熟市场为对比研究对象,引入FIGARCH模型捕获金融收益条件波动率的长记性特征;针对金融时间序列的有偏胖尾分布结构和分布的复杂性而非单一分布特征,引入EVT对收益率分布的极值尾部进行建模,以此来开展金融市场EVTVaR动态风险测度;然后运用Kupiec[26]和Christoffersen提出的似然比率
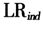 和
和 对风险测度准确性进行稳健性检验[26-28],实证考察胖尾分布与条件波动率长记忆性下风险模型在样本内测度的准确性与精度,以及样本外的推广能力。
对风险测度准确性进行稳健性检验[26-28],实证考察胖尾分布与条件波动率长记忆性下风险模型在样本内测度的准确性与精度,以及样本外的推广能力。
最后,就所掌握的文献而言,目前的大多数研究仅仅运用EVT与GARCH簇模型(如GARCH、GJR-GARCH)结合来研究金融市场风险测度方法[22-23,28-30],并依据VaR失败比率来确定风险模型的准确性与精度,很少见到运用规范、完整的返回测试(back-testing)技术来得到相应的检验结果,没有见到运用能够捕获金融市场收益条件波动率长记忆性这一重要典型事实的FIGARCH模型与EVT结合,对成熟资本市场与我国新兴市场的风险测度进行实证对比研究;尤其是在对极值尾部门槛值(extreme tail threshold)的选取上,既不是采用超均值函数(mean excess function,MEF)图方法[31],也不是运用10%最大损失值作为门槛值,而是结合两种方法来确定最优门槛值。另外,不仅选取的样本是目前所见研究中最大的样本,而且也得到了一些具有重要价值的实证结果,即基于EVT与FIGARCH的风险测度模型不仅在样本内表现出准确的测度能力,而且样本外也呈现出优越的预测推广能力,这为典型事实条件下金融风险管理理论研究与实践提供了一定的决策借鉴。由此可见,与其他文献相比,所具有的差异性是显而易见的。
1样本选取及条件收益分布的统计特征
由于研究不同类型市场的动态极值风险测度的准确性及其效果对比,所以,选取新兴市场的中国大陆上证综指(SSEC)和成熟市场的标准普尔指数(S&P500)、纳斯达克指数(Nasdaq),以及美国10年期连续国债指数(T-bond)四种指数作为代表性的研究对象,样本期为1990年12月19日(上证综指编制基准日)-2010年7月9日。由于不同市场开市、休市情况不一致,对数据进行了初步的加工处理,处理方法为:如果某一个市场当日开市交易,另一个市场休市,那么对另一个市场就以上一个交易日的收盘价代替当日的收盘价补齐,以保证数据的一致性,共计得到5 083个交易日的收盘指数价格。同时,为了检验风险测度模型的样本外推广能力,先留出最后1 000天数据作为样本外模型预测推广能力的稳健性(robustness)检验,其余4 083天数据作为样本内风险测度模型的实证建模与分析。

4种指数条件收益的波动性状况及统计特征如图1和表1所示。从图1和表1可以观察到:虽然4种指数的条件收益在分布与波动性存在较大的差别,但是4种指数收益率的J-B值都在1%的显著性水平下非常显著,都拒绝有效市场假说的正态分布假设;所有序列的偏度(skewness)都在1%的水平下显著,虽然在偏度方向上存在着不同,但4种指数条件收益均呈现出明显的有偏胖尾分布类型特征;Q(16)统计量检验表明4种指数收益都明显拒绝无自相关性;经过BDS统计量检验发现,4种指数的条件收益均拒绝独立同分布特征,说明金融条件收益并非是一个同分布序列。
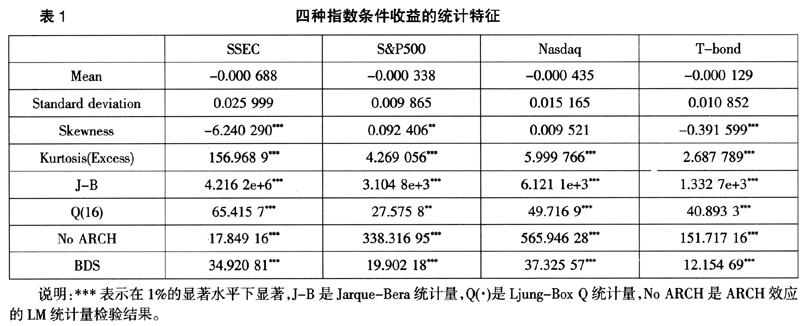

这些统计检验结果进一步证实,无论是成熟资本市场,还是新兴市场收益率序列均存在尖峰胖尾、长记忆性等典型事实特征,也就要求对金融收益描述必须对这些特征进行分析,从而也表明金融风险管理必须以这些典型事实为约束条件。
2胖尾分布与波动长记忆约束下的EVT-VaR测度方法
2.1金融市场动态风险测度的基本方法


2.2金融收益条件均值与条件波动率的建模方法
条件波动率的长记忆特征是金融风险管理中一个极其重要的典型事实,有效的风险管理技术必须将其纳入约束框架之中[5];同时,大量的实证结果也表明,金融收益的条件波动率 时间序列表现出明显的长程记忆性特征。因此,引入Bailie et al.[15]提出的FIGARCH(p,d,q)模型,其数学模型如下
时间序列表现出明显的长程记忆性特征。因此,引入Bailie et al.[15]提出的FIGARCH(p,d,q)模型,其数学模型如下

然而,在金融计量研究中,一般认为使用一阶模型就能充分反应金融数据的自相关与波动性信息[33],因此,在滞后阶的选取上均选取滞后一阶,即采用条件波动率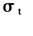 的FIGARCH(1,d,1)模型。其数学模型如下
的FIGARCH(1,d,1)模型。其数学模型如下

2.3基于EVT的金融收益极值尾部建模方法
EVT作为对金融收益尾部建模的重要方法,在尾部建模上有两种极值模型,即传统的分块最大值模型(the block maxima models,BMM)和提高门限模型(peaks over threshold,POT)[4]。当尾部数据很少时,POT仍然具有很高有效性,因而考虑使用EVT中POT模型对极值尾部进行建模分析。
根据概率论原理,给定一个门槛值u,对于超过门槛值u的变量的分布函数
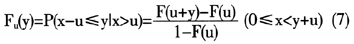
根据Haan[31]和Pickands[35]的证明,对于充分高的门槛值u(u→∞),超过门槛值u的数据近似服从EVT中的广义帕累托分布(generalized pareto distribution,GPD)簇。GPD分布簇函数的数学表达式为
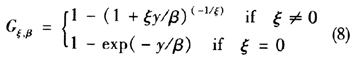
其中,β>0,1+ξy/β>0。ξ是GPD的尾部参数(tail parameter)或称尾部指数(tail index),β是标度参数(scale parameter)。参数ξ描述了概率分布的尾部特征,如果尾部参数ξ>0,则分布为胖尾分布,如学生t分布、Burr分布以及对数Gamma分布等;如果ξ<0,则该分布属于短尾分布,如均匀分布(uniform distribution)、Beta分布;如果ξ=0,则属于正态分布、对数正态分布以及指数分布形式等[4]。

在估计GPD参数时,先要确定出适当的POT门槛值u。这里需要指出的是,u的选择尤其重要,根据GPD要求,门槛取值必须相当的高,以保证方差低,但是门槛取值过高,极值数据就很少,会影响GPD估计效果;相反,门槛取值过小,落入尾部的数据多,又与GPD要求有差距。Neftci[8]把1.65σ当作门槛,超过1.65σ的值被当作极值;DuMouchel[32]认为选择10%左右的数据作为极值,与GPD的拟合效果较好。
在这里也需要说明的是,到目前为止,还没有一个确定最优门槛值的数学理论模型[9]。目前,也有相当一部分学者采用超均值函数(mean excess function,MEF)图来确定门槛值[31],MEF数学模型如下

根据(u, (u))点得到MEF图,如果MEF图向上倾斜,那么超过u的变量具有GPD分布特征;如果MEF图向下倾斜,超过u的变量是短尾分布;如果MEF图为水平线,超过u的变量服从指数分布。若标准收益的尾部服从EVT的GPD,当q>1-k/n时,得到标准收益序列q分位数值为
(u))点得到MEF图,如果MEF图向上倾斜,那么超过u的变量具有GPD分布特征;如果MEF图向下倾斜,超过u的变量是短尾分布;如果MEF图为水平线,超过u的变量服从指数分布。若标准收益的尾部服从EVT的GPD,当q>1-k/n时,得到标准收益序列q分位数值为

综合以上推导过程,就可以计算出第t日对第t+1日的动态极值风险(EVT-VaR)测度值

正如前文所分析的那样,由于标准收益序列服从的分布不同导致 取值不同,从而引起动态风险测度结果存在着差异。为了对比不同风险测度方法的结果,本文也对标准收益服从正态分布、学生t分布(student-t distribution)条件下的风险进行测度分析。若标准收益序列服从标准正态分布时,
取值不同,从而引起动态风险测度结果存在着差异。为了对比不同风险测度方法的结果,本文也对标准收益服从正态分布、学生t分布(student-t distribution)条件下的风险进行测度分析。若标准收益序列服从标准正态分布时,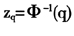 ,Φ(x)为标准正态分布的分布函数;若标准收益序列服从学生t分布时,
,Φ(x)为标准正态分布的分布函数;若标准收益序列服从学生t分布时, ,
,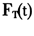 表示自由度为v的学生t分布函数。
表示自由度为v的学生t分布函数。
在这里,需要补充说明的是,由于SKST具有比学生t分布更能捕获金融收益分布的有偏形态,近年来许多学者运用SKST分布来测度金融风险并取得了较好的研究效果,也使得SKST分布成为金融风险测度研究中使用的一种重要方法[7,19]。为了对比基于EVT风险测度模型与其他模型的精度与可靠性,也对金融标准收益分布的SKST假设进行探讨。

λ是学生t分布的偏度系数,v是学生t分布的自由度,Γ(·)为Gamma分布函数。
2.4金融市场EVT-VaR模型准确性的Back-testing检验方法


但是,实际上,风险测度失败情况之间也可能是相依的(dependence),某一次出现测度失败与否可能与前一次测度失败与否的情况是非独立的。仅使用Kupiec的似然比率统计量 检验也就存在明显的不足。基于此,Christoffersen构造出依概率分布服从自由度为1的卡方分布的独立性统计量
检验也就存在明显的不足。基于此,Christoffersen构造出依概率分布服从自由度为1的卡方分布的独立性统计量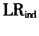 ,其零假设为
,其零假设为 :某天风险模型测度失败与前一天是独立的。
:某天风险模型测度失败与前一天是独立的。


3实证结果与分析
在AR(1)-FIGARCH(1,d,1)模型的参数估计过程中,由于无法确定标准收益zt服从哪种分布形式,因此在模型的参数估计方法上,没有采用常规的极大似然估计方法(maximum likelihood estimation,MLE),而是运用一种“让数据自己说话”的“伪极大似然估计方法”(quasi maximum likelihood estimation,QMLE)估计模型参数。部分参数估计结果见表2,从表2可以看到,四种综合指数的d∈(0,1),并且都在1%的显著性水平显著不为零,表明四种指数条件波动率均具有长期记忆性特征,从而说明构建的模型具有一定的可靠性。

在这里,仅以中国沪市上证综指(SSEC)为例,展示金融资产收益的条件波动率 与标准收益
与标准收益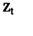 的波动状况。图2为SSEC条件波动率与标准收益率的时间序列图。比较图1与图2可以较为直观地看出,标准收益
的波动状况。图2为SSEC条件波动率与标准收益率的时间序列图。比较图1与图2可以较为直观地看出,标准收益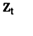 较原始收益率
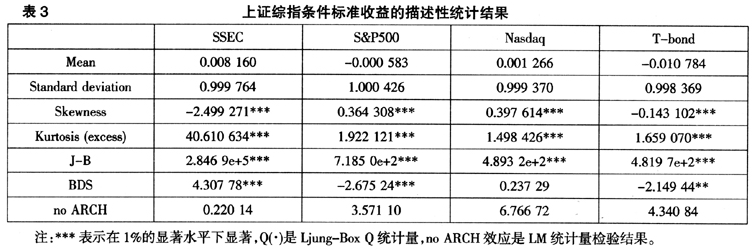
较原始收益率 序列更为平稳。表3出示的是标准收益序列的描述性统计结果,从表3可以看出,所有的标准收益均值接近为0,方差为1;所有的标准收益都具有胖尾、尖峰分布特征,标准收益与原始条件收益一样也非正态分布,偏度方向也没有发生变化,说明金融条件收益
序列更为平稳。表3出示的是标准收益序列的描述性统计结果,从表3可以看出,所有的标准收益均值接近为0,方差为1;所有的标准收益都具有胖尾、尖峰分布特征,标准收益与原始条件收益一样也非正态分布,偏度方向也没有发生变化,说明金融条件收益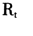 的严重胖尾特征,必然导致标准收益
的严重胖尾特征,必然导致标准收益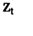 分布的胖尾性;只有Nasdaq指数标准收益都通过了BDS检验,说明并非所有的标准收益都是i. i. d.序列。因此,可以认为标准收益仍然呈现出有偏胖尾且非同一分布形态,运用EVT对标准收益的尾部具有理论上的优越性。基于此,下文将运用EVT对其尾部进行建模分析。
分布的胖尾性;只有Nasdaq指数标准收益都通过了BDS检验,说明并非所有的标准收益都是i. i. d.序列。因此,可以认为标准收益仍然呈现出有偏胖尾且非同一分布形态,运用EVT对标准收益的尾部具有理论上的优越性。基于此,下文将运用EVT对其尾部进行建模分析。

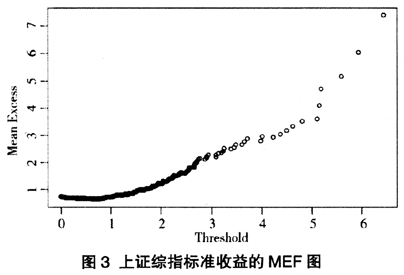
正如前文所述,采用MEF图方法与选择10%的最大值作为门槛值(threshold)两种方法的结合来选择门槛值。图3是上证综指的标准收益的MEF图。从图3可以直观看出,大约从1左右开始,MEF是斜向上的,说明其近似服从GPD分布。而选择10%的极大值为门槛值,得到u=1.06,也在1左右。综合两种结果,说明超过u=1.06的收益尾部近似服从GPD分布。
在对金融标准收益尾部的EVT建模研究中,假设尾部极值个数为k,门槛值为u,运用QMLE估计标准收益分布极值尾部的GPD参数。图4(见下页)是上证综指标准收益尾部经验分布与GPD分布拟合效果图。从图4可以很直观地看出,标准收益的GPD与经验分布有较好的拟合效果,说明运用EVT中GPD分布在金融市场收益尾部的拟合上具有可靠性。

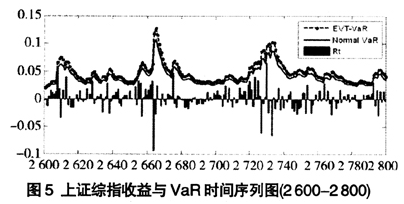
在这里,需要说明的是,q的取值大小,由投资者对待风险的态度以及投资者的经济实力所决定[2,8-10]。由于是对金融市场动态极值风险进行测度,所以选取q=99%。根据式(13)得到动态极值风险序列。为了更直观地展示测度出动态EVT风险序列,仅仅出示第2 600-2 800天上证综指的动态风险值与条件收益直观图(见图5)。从图5中可以直观看出,风险序列比条件收益序列要大,只有很少地方收益高于风险值VaR,直观地说明了模型在测度风险方面具有一定的可靠性。
对于风险模型的样本内测度的准确性,采用Back-testing方法[4]进行检验。表4是样本内风险测度准确性的Back-testing检验结果。分析表4可以得到以下实证结论。
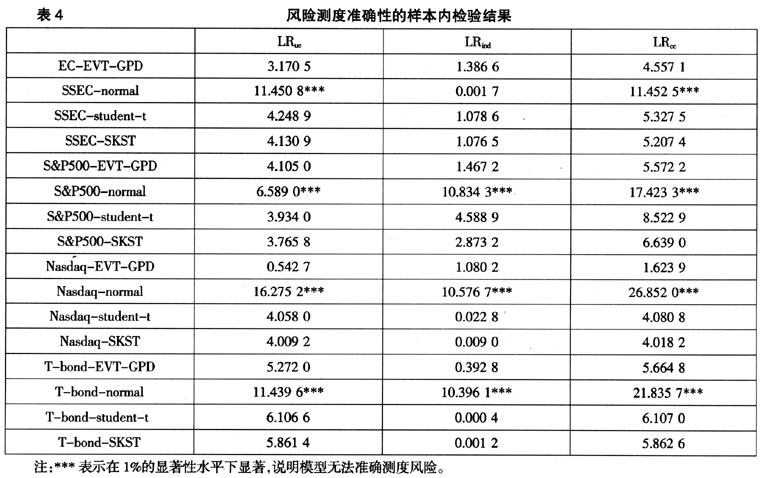
1)基于金融条件收益率的胖尾分布特征与条件波动率的长记忆性构建的风险测度模型,能够准确测度中国沪市上证综指、标准普尔500指数、纳期达克指数和美国10年期国债指数的市场风险,这个结果为金融市场管理当局、金融资产投资者测度市场风险、加强风险管理提供了实证依据。
2)从标准收益的分布情况来看,无论是新兴市场还是成熟发达市场,所有正态分布假设下的风险模型都没有通过检验,说明正态分布不能有效刻画标准收益的分布,不能准确测度金融市场极端风险,从而说明正态分布假设下的风险测度指标体系会低估风险,导致风险管理失效。
3)虽然学生t分布较正态分布具有更为肥胖的尾部,假设标准收益服从学生t分布时也能通过返回测试检验;但是从 的统计量大小来看,有偏学生t分布(SKST)假设却又比学生t分布假设具有更加优越的风险测度能力。分析原因可能是,与学生t分布相比,有偏学生t分布(SKST)更能捕获金融收益的有偏分布特征,因而表现出更高的精度。但是,从
的统计量大小来看,有偏学生t分布(SKST)假设却又比学生t分布假设具有更加优越的风险测度能力。分析原因可能是,与学生t分布相比,有偏学生t分布(SKST)更能捕获金融收益的有偏分布特征,因而表现出更高的精度。但是,从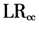 的统计量大小来看,无论是有偏学生t分布假设还是学生t分布假设,EVT-GPD比它们的统计量仍然都要小,说明EVT-GPD更能捕获收益尾部的分布特征。
的统计量大小来看,无论是有偏学生t分布假设还是学生t分布假设,EVT-GPD比它们的统计量仍然都要小,说明EVT-GPD更能捕获收益尾部的分布特征。
基于以上结果不难看出,有偏胖尾分布(如有偏学生t分布)比对称正态分布、学生t分布条件下构建的风险测度方法更具有可行性,而极值理论EVT技术对极值尾部建模又比假定一个确定分布在测度风险方面表现出更大的优越性。
既然如此,在样本内VaR测度方面,基于条件收益率胖尾分布与条件波动率长记忆性特征的EVT-GPD风险测度模型,具有比本文使用的其他模型更为优越的风险测度能力。那么,在样本外,此模型是否也具有较好的预测推广能力而使模型更具稳健性呢?
基于此,选择最后1 000天样本,仍然运用Back-testing中的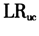 ,
,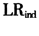 和
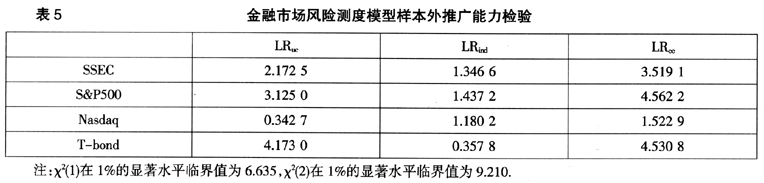
和 检验指标对EVT-GPD模型风险预测推广能力进行检验。由于篇幅限制,仅出示EVT-GPD风险测度模型的检验结果,结果见表5。从表5可以发现,在胖尾分布与波动率长记忆性条件下EVT-GPD风险测度模型,对于各个市场均在1%的显著性水平下都通过Back-testing检验,不仅说明了基于EVT-FIGARCH模型的VaR测度方法在样本外同样具有可靠的推广能力,从而也说明风险模型具有样本外的稳健性,同时还说明了基于EVT-FIGARCH的VaR模型测度西方成熟发达金融市场与中国新兴市场风险在可靠性与精度方面并未展示出实质性差异。
检验指标对EVT-GPD模型风险预测推广能力进行检验。由于篇幅限制,仅出示EVT-GPD风险测度模型的检验结果,结果见表5。从表5可以发现,在胖尾分布与波动率长记忆性条件下EVT-GPD风险测度模型,对于各个市场均在1%的显著性水平下都通过Back-testing检验,不仅说明了基于EVT-FIGARCH模型的VaR测度方法在样本外同样具有可靠的推广能力,从而也说明风险模型具有样本外的稳健性,同时还说明了基于EVT-FIGARCH的VaR模型测度西方成熟发达金融市场与中国新兴市场风险在可靠性与精度方面并未展示出实质性差异。
4结束语
金融资产价格条件收益率展示出有偏胖尾的复杂分布形态以及条件波动率呈现的长记忆性特征,一直都是金融学理论研究的重要内容。通过运用FIGARCH对金融资产收益条件波动率的长期记忆性建模分析,进而运用EVT对具有复杂有偏胖尾的标准收益尾部进行建模来测度风险,然后运用返回测试(back-testing)方法对构建的风险测度模型在样本内测度准确性与样本外的预测推广能力进行了稳健性检验。
通过实证研究得到了一些重要的结果:(1)金融资产收益与标准收益率,无论是发达成熟的西方市场如纳斯达克股市,还是诸如中国沪市等新兴市场,均表现比正态分布更具有尖峰、肥胖的特征,表明EMH条件下的正态分布假设确实与金融市场实际收益分布明显不相符合,运用传统的风险测度方法会低估风险,金融风险管理必须引入非正态分布的有偏胖尾分布形式,以提高风险管理的效果;(2)四种指数收益条件波动率呈现出异方差与长期记忆性特征,这表明典型事实存在于不同类型与不同国家的金融市场当中,风险管理必须以这些典型事实为约束条件进行;虽然具有有偏分布形态特征的SKST在风险测度的精度上表现出了比学生t分布更为卓越的测度效果,也通过了样本内风险测度准确性的Back-testing检验,但EVT对尾部建模的风险测度模型却表现出比SKST更高的准确性与精度,这充分说明了对金融资产的条件收益率更可能是复杂分布形态而非单一分布;(3)结合EVT与FIGARCH的风险模型,在测度中国大陆沪市、标准普尔500指数、纳斯达克指数及美国10年期国债市场的风险准确性方面,无论是样本内的风险测度能力,还是样本外的预测推广能力,都表现出明显的优越性与重要性。
就政府金融市场管理当局和投资者而言,随着金融市场和计算机信息技术的发展,必将出现更多目前尚未认知的“典型事实”,典型事实的增多也必将使风险管理面临“维数灾难”问题,这也必将使金融市场风险管理面临着更大更新的挑战。因此,强化对金融市场典型事实的探讨,建立更为有效度量市场风险的计量模型与方法,采取行之有效措施,防止金融市场出现大起大落,进而防范极端风险灾难危机的发生,维护经济安全,促进经济发展与繁荣,是一项长期而又艰巨的任务。
最后需要说明的是,尽管本文仅仅以四种指数为例,探讨的是成熟市场与新兴金融市场风险测度问题,但研究技术与相关结论,仍然可以为金融市场并非完全有效条件下政府金融市场管理当局、金融机构与投资者在风险管理方面提供一定的决策借鉴。
参看文献:
[1]Morgan J P. Inc. 
[2]McNeil A, Frey R. Estimation of tail-related risk measures for heteroscedastic financial time series: An extreme value approach[J]. Journal of Empirical Finance, 2000,(7): 271-300.
[3]Basle Committee. Overview of the Amendment of the Capital Accord to Incorporate Market Risk[M]. Basle Committee on Banking Supervision, 1996.
[4]Kevin D. Measuring Market Risk— ed[M]. Chichester: John Wiley & Sons, Ltd. 2005.
ed[M]. Chichester: John Wiley & Sons, Ltd. 2005.
[5]Cont R. Empirical properties of assets returns: Stylized facts and statistical issues[J]. Quantitative Finance, 2001,(1): 223-236.
[6]Aas, Haft. The generalised hyperbolic skew student's tdistribution[J]. Journal of Financial Econometrics, 2006,(4): 275-309.
[7]魏宇.股票市场的极值风险测度及后验分析研究[J].管理科学学报,2008,(1):78—88.
Wei Yu. EVT risk measures and its backtesting in stock markets[J]. Journal of Management Sciences in China, 2008,(1): 78-88.(in Chinese)
[8]Neftci S. Value at risk calculations, extreme events and tail estimation[J]. The Journal of Derivations, 2000,(spring): 1-15.
[9]黄大山,刘明军,卢祖帝.极值风险E—VaR及深圳成指实证研究[J].管理评论,2005,17(6):16—24.
Huang Dashan, Liu Mingjun, Lu Zudi. Extreme VaR and its empirical analysis of Shenzhen stock index[J]. Management Review, 2005, 17(6): 16-24.(in Chinese)
[10]Ramazan G, Faruk S. Extreme value theory and value-at-risk: Relative performance in emerging markets[J]. International Journal of Forecasting, 2004,(20): 287-303.
[11]Bystrom. Extreme value theory and extremely large electricity price changes[J]. International Review of Economics and Finance, 2005,(14): 41-55.
[12]Huang Y C, Lin B J. Value-at-risk analysis for Taiwan stock index futures: Fat tail and conditional asymmetries in return innovations[J]. Review of Quantitative Finance and Accounting 2004,(22): 79-95.
[13]Fernandez. Risk management under extreme events[J].International Review of Financial Analysis, 2005,(14): 113-148.
[14]余素红,张世英,宋军.基于GARCH模型和SV模型的VaR比较[J].管理科学学报,2004,7(5):61-65.
Yu Suhong, Zhang Shiying, Song Jun. Comparison of VaR based on GARCH and SV models[J]. Journal of Management Sciences in China, 2004, 7(5): 61-65.(in Chinese)
[15]Baillie R T, Bollerslev T, Mikkelsen H O. Fractionally integrated generalized autoregressive conditional heteroskedasticity[J]. Journal of Econometrics, 1996,(74): 3-30.
[16]Grau T M N. Modeling Daily Value-at-Risk Using FIGARCH Type Models[R]. University of Alicante, Working Paper, 2002.
[17]Beine M, Laurent S, Lecourt C. Accounting for conditional leptokurtosis and closing days effect in FIGARCH models of daily exchange rates[J]. Applied Financial Economics, 2002,(12): 589-600.
[18]Wu Ping-Tsung, Shieh Shwu-Jane. Value-at-risk analysis for long-term interest rate futures: Fat-tail and long memory in return innovations[J]. Journal of Empirical Finance, 2007,(14): 248-259.
[19]Hansen B. Autoregressive conditional density estimation[J]. International Economic Review, 1994, 35(3), 705-730.
[20]王吉培,旷志平.偏态t分布下FIGARCH模型的动态VaR计算[J].统计与信息论坛,2009,24(5):75—79.
Wang Jipei, Kuang Zhiping. Calculation of dynamic VaR based on the skew student t distribution of FIGARCH model[J].Statistics & Information Forum, 2009, 24(5): 75-79.(in Chinese)
[21]徐炜,黄炎龙.GARCH模型与VaR的度量研究[J].数量经济技术经济研究,2008,(1):120-132.
Xu Wei, Huang Yanlong. Empirical analysis on GARCH-type models and VaR[J]. The Journal of Quantitative & Technical Economics, 2008,(1): 120-132.(in Chinese)
[22]肖智,傅肖肖,钟波.基于EVT-POT-FIGARCH的动态VaR风险测度[J].南开管理评论,2008,(11):100-104.
Xiao Zhi, Fu Xiaoxiao, Zhong Bo. Dynamic VaR risk measures based on EVT-POT-FIGARCH[J]. Nankai Business Review, 2008,(11): 100-104.(in Chinese)
[23]林宇,魏宇,黄登仕.基于GJR模型的EVT动态风险测度研究[J].系统工程学报,2008,23(1):45-51.
Lin Yu, Wei Yu, Huang Dengshi. Study on dynamic risk measurement based on GJR and EVT[J]. Journal of Systems Engineering 2008, 23(1): 45-51.(in Chinese)
[24]王春峰,张庆翠.中国股市波动性过程中的长期记忆性实证研究[J].系统工程,2004,(1):78-83.
Wang Chunfeng, Zhang Qingcui. Modeling long memory in Chinese stock market volatility[J]. System Engineering, 2004,(1): 78-83.(in Chinese)
[25]Hong Y M, et al. Granger causality in risk and detection of extreme risk spillover between financial markets[J]. Journal of Econometrics, 2009, 150(2): 271-287.
[26]Kupiec P. Techniques for verifying the accuracy of risk measurement models[J]. Journal of Derivatives, 1995,(3): 73-84.
[27]Christoffersen F. Elements of Financial Risk Management[M]. McGill University and CIRANO, 2002.
[28]Konstantinos T, Athansios K, Richard A B. Extreme risk and value at risk in the German stock market[J]. The European Journal of Finance, 2007, 13(4): 373-395.
[29]Brooks C, Persand G. The effect of asymmetries on stock index return value-at-risk estimates[J]. Journal of Risk Finance, 2003,(4): 29-43.
[30]Glosten L R, Jagannathan R, Runkle D E. On the relation between the expected value and the volatility of the nominal excess return on stocks[J]. The Journal of Finance, 1993, VOL. XLVIII(5): 193-209.
[31]Stelios D B, Dimitris A G. Estimation of value-at-risk by extreme value and conventional methods: A comparative evaluation of their predictive performance[J]. Int. Fin. Markets, Inst and Money, 2005,(15): 209-228.
[32]DuMouchel W M. Estimating the stable index-in order to measure tail thickness: A critique[J]. Annals of Statistics, 1983,(11): 1019-1031.
[33]Lamoureux, William. Forecasting stock-return variance: Toward an understanding of stochastic implied volatilities[J]. Review of Financial Studies, 1993, 6(2): 293-326.
[34]Haan L. Residual life time at great age[J]. Annals of Probability, 1974,(2): 792-804.
[35]Pickand A. Statistical inference using extreme order statistics[J]. Annals of Statistics, 1975,(3): 119-131.
