基于核密度估计的非线性时间序列聚类

内容提要：本文研究的是时间序列的聚类问题。由于现实世界中时间序列多数是非线性的，而现有的时间序列聚类问题大都是基于线性时间序列模型进行聚类的，本文提出了可以用于非线性时间序列的聚类方法。以时间序列的二维核密度估计之间的相似性作为非线性时间序列的距离度量，该距离度量方式是一种非参数的距离度量方法，考虑到了时间序列自相关结构的差异，能够粗糙地识别时间序列形状和动态相关结构的相似性。与理论研究结果相一致，我们的模拟实验结果也验证了这种距离度量的有效性。
    关键词：非线性时间序列 聚类 核密度估计
    作者简介：张贝贝，女，河南济源人，中国人民大学博士生。
    1引言
    时间序列的聚类和分类能够为不同领域的实际问题提供很多重要的信息。在天文学上，Kakizawa等(1998)[1]为了识别地震和爆炸这两类事件建立了时间序列之间的相似性度量；Macchiato等(1995)[2]根据每日气温的时间序列数据来进行区域聚类；Cowpertwait和Cox(1992)[3]将时间序列聚类应用到降雨问题中。除此之外，在医药，金融，工程等领域也能够找到很多时间序列聚类的相关工作。
    聚类是无指导学习的一种方法，其目的是通过辨识数据间的结构特征，使得数据在类内相似性最大、类间的相似性最小。当我们能够观测到大量的时间序列样本时，时间序列聚类的问题也就产生了，我们想要将大量的时间序列纵向数据聚成不同的类别。与静态数据不同，时间序列数据具有相关性结构，故对其进行聚类分析有着很大的复杂性。近年来涌现出许多时间序列聚类方法，在这里不再一一列举，有兴趣的读者可以参考文献[4]，它比较全面系统地分类并概括了时间序列聚类的各种方法和在各个领域的应用。
    在聚类问题中，距离的度量是最关键的问题，距离度量方式的选择应该考虑聚类的最终目的，以便距离能够获得与聚类目的直接相关的观测之间的特殊差异。本文我们聚类的目的是为了将有相同动态行为的时间序列聚成一组。大多数主流的时间序列的聚类方法基本上是针对线性时间序列的，聚类的前提是假设平稳时间序列能够由线性模型来拟合。例如[5-8]等文章中提到的方法。而事实上，线性模型只是描述未知的时间序列动态关系的第一步，因为真实的世界是非线性的。所以使用经典的基于ARMA模型的参数聚类方法来对非线性的时间序列数据聚类显然是不适合的。另外，现有的非参数的时间序列，是基于时间序列的自相关函数(ACF)和偏自相关函数(PACF)的，虽然不假设任何时间序列模型，但ACF和PACF度量的只是时间序列的线性相关关系。Granger与Lin(1994)[9]发现一般的相关函数例如ACF和PACF，用来度量非线性的相关关系时是不充分的；而且有些非线性时间序列的ACF和PACF会表现的像白噪声，这样的相关函数会误导我们得到非线性时间序列没有自相关的错误结论。所以我们就考虑去发展一种针对非线性时间序列的专门的聚类方法。
    直方图或密度函数是很有用的，可以用来检查数据集的基本分布状况，包括数量，峰值和槽的位置和密度函数的对称性等。如果时间序列来自一个平稳的分布，密度估计就能够提供一些很有用的时间序列的统计分布特征。来自同一个随机过程的两个序列通常具有相似的概率分布，基于这个考虑，我们提出一种根据概率密度函数的接近程度来定义来度量两个时间序列的距离的方法，概率密度函数可以通过核函数进行非参数估计，同时在距离度量中加入时间序列的相关结构特征。
    本文的结构组织如下：第一部分，我们回顾了核密度估计，包括一维和高维及针对相关性数据的情况。第二部分，详细介绍了所提出的基于核密度估计的距离度量，并进行了分析。第三部分，通过模拟实验呈现了我们提出的距离度量聚类的结果，验证了其用于聚类的有效性。最后是全文结论。
    2时间序列的核密度估计
    2.1一维核密度估计
    
    
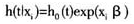
    跟一维情况一样，我们必须做一些核函数和带宽参数的选择来构造多维核密度估计。但是，向高维的扩展就意味着要更高的自由度。首先，d维的核函数得选择；其次，每一维中平滑参数的选择。所以高维的核密度估计的复杂性在于更多的参数需要选择，在应用中有冗长的计算时间和数学处理难度的问题。不仅如此，高维的密度估计也面临着维数灾难的问题。这里不再详细介绍，有兴趣的读者可参考[12]，有对高维核密度估计更多的细节的介绍。本文研究的是时间序列的核密度估计。时间序列是具有相关性的数据，在[13]的文献中研究了数据的相关结构对核密度估计的影响，[12]、[14]、[15]研究了一些线性过程下核密度估计的一致性和渐进正态性，但是独立样本下的所有的技术几乎都能够被扩展到混合平稳过程。所以本文我们暂不考虑时间序列的相关结构对核密度估计的影响。
    3基于核密度估计的聚类方法
    
    
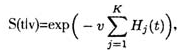
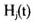
    *选择一种传统的聚类方法
    在确定了距离矩阵之后，我们选择使用比较经典的非分层决策树的方法——K均值算法，在这个方法中，首先，决定k个聚类的初始集合，计算每个时间序列到各个聚类中心的距离，不断的移动每个时间序列到离聚类中心的距离最近的那个类别，然后重新计算新构造的聚类的中心，不断迭代这个再分配过程，直到没有时间序列被再分配，这时候最终得到的聚类就是我们所要的。
    
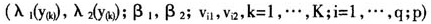
    图2两变量联合核密度估计图
    4模拟实验
    我们首先在非线性自回归模型(M1-M8)下调查该距离度量的行为。非线性自回归模型，是一个广泛应用时间序列族。为了对比试验效果，我们也考虑了一个最简单的线性时间序列模型——AR(1)模型。为了评价聚类效果，本实验基于已知真实样本所属类别情况下的评估标准——Similarity Measure，它的范围从0到1，越大的值意味着聚类效果越好。每次试验做聚类15次，聚类结果的Similarity Measure的最小值、平均值和最大值被记录。Similarity Measure的定义如下：
    
    
    
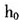
    表1当滞(lag)改变的聚类性能对比
    
    当距离度量时使用的二维的边际核密度估计的滞等于该序列真实的滞(lag=1)时，这个聚类结果能够非常好地将来自不同组的时间序列分开。所以，只要能够准确把握时间序列的自相关关系的阶数，那么这个距离度量就是一种效果非常好的时间序列的聚类方法。
    但随着滞的增加，这个聚类结果不断变差。这个现象可以通过时间序列模型的结构来解释，模拟实验中的数据结构我们事先是知道的，即lag=1的自相关结构，所以我们知道，当滞(lag)不断增加的时候，自相关结构逐渐变弱，这时不同时间序列的自相关结构的差异变的不显著，这个现象也证明了我们提出的基于二维的核密度估计的距离度量了时间序列自相关性结构之间的差异。
    5结论
    本文我们提出了一种基于估计时间序列的二维样本的核密度估计的非线性时间序列相似性的方法，这是一种非参数的距离度量方式，它能够粗糙地识别时间序列形状和动态结构的相似性；与理论结果一致，我们的模拟实验结果也验证了这种距离度量的有效性。我们未来的工作是，进一步挖掘该方法在实际问题中的应用，希望能够解决更多实际生活中的聚类问题。
    参考文献：
    [1]Y Kakizawa, et al (1998). Discrimination and Clustering for Multivariate Time Series. Journal of the American Statistical Association, 93(441):328-340.
    [2]Macchiato et al (1995). Time modelling and spatial clustering of daily ambient temperature: an application in Southern Italy, Environmetrics 6:31-53.
    [3]Trevor F. Cox and Paul S.P. Cowpertwait (1992). Clustering Population Means Under Heterogeneity of Variance. Journal of the Royal Statistical Society. Series D (The Statistician), Vol. 41(5):591-598.
    [4]T.W. Liao (2005), Clustering time series data-a survey, Pattern Recognition 38:1857-1874.
    [5]Maharaj A (2000). Clusters of time series[J], J. Classification 17:297-314.
    [6]Piccolo D (1990). A distance measure for classifying ARIMA models[J], Journal of TimeSeries Analysis, 11,153-164.
    [7]Piccolo D (2007). Statistical issues on the AR metric in time series analysis[J], Proceedings of the SIS 2007 intermediate conference "Risk and Prediction", 221-232.
    [8]Kalpakis K, Gada D, Puttagunta V (2001). Distance measures for effective clustering of ARIMA time-series[C], Proceedings of the 2001 IEEE International Conference on Data Mining, San Jose, CA, November 29-December 2, pp.273-280.
    [9]Granger, C.W.J., Lin J.L. (1994): Using the Mutual Information Coefficient to Identify Lags in Nonlinear Models[J], Journal of Time Series Analysis, 15,371-384.
    [10]B.W. Silverman (1986), Density Estimation for Statistics and Data Analysis. Chapman & Hall.
    [11]Tjstheim, D. (1996). Measures and Tests of Independence: A Survey. Statistics, 28,249-284.
    [12]David W. Scott (1992). Multivariate density estimation: theory, practice, and visualization. Wiley Series in Probability & Mathematical Statistics.
    [13]Claeskens, G. and Hall, P. (2002). Effect of dependence on stochastic measures of accuracy of density estimators. Ann. Statist. 30:431-454.
    [14]Chanda, K.C. (1983). Density estimation for linear processes, Ann. Inst. Statist. Math., 35:439-446.
    [15]Hallin, M. and Tran, L.T. (1996). Kernel density estimation for linear processes: Asymptotic normality and optimal bandwidth derivation. Ann. Inst. Statist. Math. 48:430-448.
    [16]Lu, Z. (2001). Asymptotic normality of kernel density estimators under dependence. Ann. Inst. Statist. Math.53:447-468.