摘 要:本文在考虑空间集聚效应情况下运用随机前沿分析法对中国区域技术效率进行测算,并运用空间面板数据模型从制度因素、经济因素、创新能力和空间效应方面实证分析了各变量对区域技术效率的影响。研究发现:考虑空间集聚效应后,东部地区技术效率有所提高,中、西部地区技术效率略有降低;中国区域技术效率存在显著的空间正相关性,且空间相关性存在一定的地域特征;空间溢出效应、市场化水平、产业结构水平对区域的技术效率具有显著促进作用。
关键词:空间集聚,技术效率,随机前沿,空间效应
基金项目:本文是国家自然科学基金项目(项目编号:70972073)和国家社会科学基金项目(项目编号:08BJY014)的阶段性成果。
一、引言
进入新世纪以来,以要素高投入为特征的粗放型经济增长模式日益受到了经济社会可持续发展的制约,以效率提高和技术进步为特征的可持续发展模式逐渐成为各界学者研究的重点。为了准确分析区域效率水平对经济增长的作用,学者们从不同角度、运用不同方法对区域技术效率进行了深入分析,得到了大量可供借鉴的研究成果。例如,颜鹏飞、王兵[1]运用DEA方法测度了中国各地区的技术效率,认为中国全要素生产率增长的主要原因是技术效率的提高;王志刚、龚六堂[2]运用SFA方法分析了中国区域技术效率和全要素生产率水平;傅晓霞、吴利学[3]运用随机前沿模型分析了影响区域技术效率的相关因素,随后傅晓霞、吴利学[4]通过比较发现与数据包络方法相比,随机前沿分析更加具有有效性和稳健性;王丽丽、范爱军[5]基于DEA方法和门限回归模型研究发现,空间集聚主要是通过技术效率来影响全要素生产率;王志平[6]基于SFA方法和主成分方法分析了我国各地区的全要素生产率以及技术效率的区域特征。
目前在分析区域技术效率过程中主要涉及三方面问题,一是生产函数设定,二是效率测算方法的选用,三是区域技术效率影响因素分析。在生产函数设定方面,几乎所有文献都是以新古典经济增长模型为基础,以资本和劳动为主要投入要素来设定生产函数;在效率测算方法选用中,目前运用最多、最成熟的是前沿分析法,即SFA和DEA方法;在分析区域技术效率影响因素时,学者们大多运用传统线性回归方法具体分析各变量对区域技术效率的作用。显然,已有文献在分析我国区域技术效率中都忽略了影响经济增长的关键性变量——空间因素。自从Krugman等成功将空间因素纳入主流经济学分析框架以来,空间维度在经济系统中的作用已为越来越多的学者所认可,以资本和劳动投入为主的传统生产函数很难把握经济增长中的空间属性,在解释当前各种经济问题时已力不从心。我国区域经济发展表明,区域经济增长不仅取决于资本、劳动等投入的增长,还受到区域空间集聚水平的影响,空间集聚具有内生性[7-8]。另外,区域间的技术知识空间溢出效应已为越来越多的学者所认知,例如舒元、才国伟[9]运用DEA方法测算了中国省域技术进步,并分析了空间技术溢出对中国区域技术进步的影响,证实了中国区域间存在较显著的技术扩散现象,但已有研究在对区域技术效率的分析中大多沿袭了传统线性模型分析方法,忽略了空间溢出效应对技术效率的影响。
针对上述两方面的问题,本文主要从生产函数设定和技术空间溢出效应两方面来拓展已有研究。第一,在生产函数设定方面,考虑到经济集聚效应对经济增长的作用,借鉴Ciccone,Hall[10]的空间集聚与区域经济增长相关模型来测算我国区域技术效率水平,并通过与传统生产函数测算的区域技术效率比较来验证经济集聚对区域经济增长和技术效率的影响;第二,考虑到传统线性回归模型在分析空间问题上的不足,本文运用面板数据空间计量经济模型分析区域间空间溢出效应对区域技术效率的作用,从而在把握传统因素作用的同时,深入理解空间效应与我国区域技术效率间的相互关系。
二、模型、方法与数据说明
1.生产函数设定
20世纪90年代以来,在Dixit-Stiglitz垄断竞争模型的基础上,以Krugman等为代表的一大批学者成功将经济系统中的空间因素纳入主流经济学研究框架,形成了著名的新经济地理学。近些年来,以Baldwin,Martin等为代表的新经济地理学者将新经济地理学模型和内生增长理论相结合构建出基于空间集聚的区域经济增长模型。
理论研究表明,与资本、劳动等生产要素一样,经济集聚是影响区域经济增长的重要因素。然而,理论模型推导过程均具有严格的前提假设条件,将其直接应用于实证分析几乎难以实现。截至目前,除研究经济活动密度与经济增长关系的Ciccone,Hall[10]模型以外,得到普遍认可、具有严密理论基础且可用于实证研究的应用模型仍鲜见于文献中。因此,本文将采用Ciccone,Hall推导得出的生产函数模型来估计区域技术效率,其柯布-道格拉斯函数形式为:
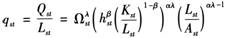 (1)
(1)
其中,Qst,Lst,Kst,Ast,hst分别为s地区在第t时刻的产出总量、劳动力总量、资本总量、地区总面积和劳动效率,Ωst为地区s在第t时刻的全要素生产率,α是单位面积资本与劳动的规模报酬,0<α≤1表示边际生产率递减,即“拥挤效应”;β是要素贡献率,0<β≤1;λ为产出密度参数。
2.随机前沿生产函数模型
已有文献对效率估计主要是基于随机前沿分析(SFA)和数据包络分析(DEA)为基础的效率估算。本文将采用随机前沿分析(SFA)来估计考虑集聚效应后的中国区域技术效率。根据Kumbhakar [11]的分析,标准的随机前沿生产函数可以表述为:
lnyit=lnf(xit,t)+vit-uit (2)
其中,vit~N(0,σv2),uit~N+(mit,σu2),mit=Zitη,σu2=exp(Zitθ),σv2=exp(Zitλ);vit为地区i在第t年生产过程的随机误差,包括测量误差以及各种不可控的随机因素;uit为地区i在第t年的生产无效率项,服从半正态分布,为非负随机变量;复合残差项uit和vit的分布相互独立,且与解释变量不相关;Zit为影响某地区技术效率的外生变量构成的向量;η为参数向量,其含义为不同地区不同时期具有不同的效率期望;σv2与σu2为常量,复合残差项的方差为σ2=σu2+σv2。根据随机前沿生产模型的定义,地区i在第t年的技术效率为:TEit=exp(-uit)。
结合本文设定的生产函数形式,随机前沿生产函数可以表示为:
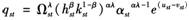 (3)
(3)
3.超越对数函数模型
本文选用超越对数函数的随机前沿模型,其具体形式如下:
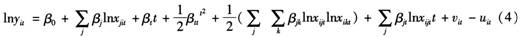
其中,lnyit是i地区第t年的对数劳均产出(i=1,2,…,N,t=1,2,…,T),lnxijt,lnxikt是第i个地区在第t年第j,k种投入要素的对数形式,它们随不同地区和时期而有所变化。本文主要包括劳均资本存量、劳均效率和区域集聚水平三种变量(j,k=1,2,3)。t是时间趋势,表示技术变化,v,u意义同上。
4.数据说明
本文使用的数据来源于《新中国五十五年统计资料汇编1949~2004》、2002~2009年《中国劳动统计年鉴》、相关年份《中国统计年鉴》及各省(直辖市、自治区)统计年鉴,研究对象包括中国30个省、直辖市或自治区(重庆市包含在四川省内)。变量取值及说明如下:
(1)地区劳均GDP:用地区GDP总量除以地区劳动力总量计算得出,其中,各年份的地区GDP总量用1952年地区GDP平减指数处理来衡量。(2)劳动效率(h):用各地区平均受教育年限来表示,类似Wang[12]等的方法,采用6岁及以上人口平均受教育年数,假定文盲半文盲、小学、初中、高中、大专以上教育程度的居民平均教育年数分别为0、6、9、12和16年。(3)劳均资本存量(k):用地区资本存量除以地区劳动力总量计算得出。文中资本存量数据使用永续盘存法核算各省(直辖市、自治区)1952~2008年资本存量数据后得到,其计算方法借鉴单豪杰[13]关于区域资本存量的核算,Kt=(1-δ)Kt-1+It,其中I为固定资本形成总额,δ为资本的平均折旧率,取值为10.96%。资本存量核算的初始年份为1952年,计算公式为K1952=I1953/(gI(1953~1957)+δ),其中gI(1953~1957)为1953~1957年固定资产投资形成的平均增长率。(4)地区集聚水平(a):用各地区劳动力总量除以地区行政区面积计算得出。
对于影响各地技术效率的变量,根据王志刚、龚六堂等[2],傅晓霞、吴利学[3],王志平[6]等的设定,本文从制度因素、经济因素、创新能力和基础设施几个方面选取区域技术效率解释变量。根据变量的可得性,选取的制度变量包括市场化指数、对外开放水平和政府财政支出;经济因素变量包括产业结构指数、固定资产投资比例;人力资本变量用教育投资来表示。(5)市场化指数(M):樊纲、王小鲁[14]指出市场化指数是政府与市场的关系、非国有经济的发展、要素市场发育程度、产品市场发育程度、市场中介组织发育和法律制度环境这五个方面的综合变量。本文的市场化指数借鉴樊纲等的中国市场化指数测算方法选取非国有经济发展、要素市场发育程度和产品市场发育程度运用主成份分析法测算得出。(6)对外开放水平(Ope):用各地区出口总量除以地区GDP总量计算得到,其中,各地区出口总量用各年人民币与美元汇率折算得出。(7)财政支出占GDP的比重(Gov):用各地区的政府财政支出除以地区GDP总量计算得到,用来表示政府投资对技术效率的作用程度。(8)产业结构指数(Arg):用各地区第一产业生产总量除以地区GDP总量计算得到。由于第一产业技术效率较低,因此我们假定该指数对技术效率影响为负。(9)固定资产投资占GDP比重(Ivs):用各地区的固定资产投资除以地区GDP总量计算得到。(10)教育投资变量(Hum):用地区教育投资总量除以地区GDP总量计算得到。(11)基础设施(Inf):用各省的公路里程密度和铁路里程密度和来表示。
三、效率估计
以1999~2008年的中国省级区域面板数据为基础,利用Frontier4.0软件进行回归,估计结果如表1中的模型(1)和(2)所示。模型(1)是采用传统模型的回归估计结果(未考虑空间集聚效应),模型(2)则是对引入空间集聚后的回归结果。比较模型(1)、(2)中的回归结果可以看出,在引入空间集聚因素后,生产无效率项u有所降低,效率变化系数η由负变为正,γ值亦有所提高,这说明引入空间集聚以后,区域技术效率存在明显的变化。比较模型(1)和(2)估算结果可以看出,考虑空间集聚因素后,东部地区中的北京、天津、上海、江苏、浙江、山东和广东等地区的技术效率明显比未考虑空间集聚效应技术效率值高,而中西部地区中的大多数省份却刚好相反,考虑空间集聚效应后的区域技术效率明显偏低,这可能是因为中国东部地区的集聚水平较高,区域集聚效应对经济增长的作用比较突出,从而提升了区域技术效率,而中西部地区的集聚水平并不明显,集聚效应对经济增长的作用仍未显现,导致了区域整体技术效率水平偏低。因此,在忽略集聚因素对经济增长影响作用的情况下测算区域技术效率会将集聚效应排除于技术效率项之外,导致测算结果的不完整性和不准确性。
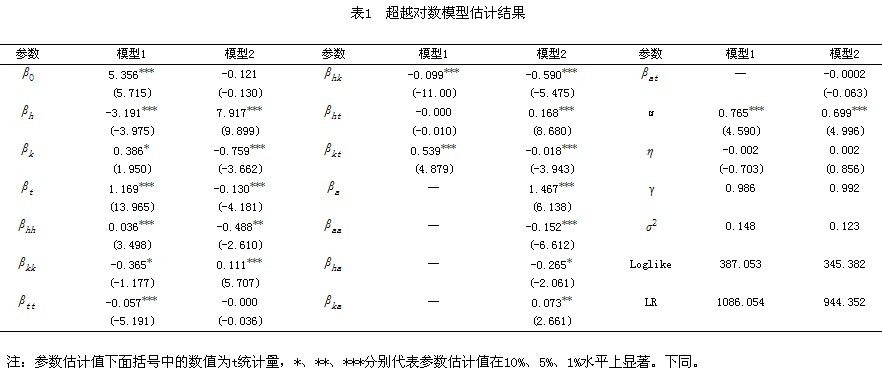
表2给出了模型(2)的部分参数的广义似然比检验结果①。假设Ⅰ是对模型(2)中空间集聚变量的似然比检验,从检验结果可看出,空间集聚对区域经济增长具有显著影响,证实了模型(2)比模型(1)具有更好的解释能力;假设Ⅱ是对模型所有二次项系数的似然比检验,该假设结论表明与柯布-道格拉斯生产函数相比,超越对数函数更适合本文的模型设定;假设Ⅲ对劳均资本存量、劳动效率、集聚水平与技术进步t的交叉项系数检验,检验结论表明技术进步受到资本、劳动效率和集聚水平的影响,即技术进步为非中性;假设Ⅳ是时变参数η=0的参数检验,检验结果表明技术效率具有时间趋势。综合表2中的假设检验结果,模型(2)及其估计方法均具有较好的解释能力。

四、区域技术效率的空间效应分析
从测算出的区域技术效率可以看出,区域技术效率具有明显的空间特征,东部地区的技术效率明显高于中部和西部地区,中部和西部地区效率水平低于全国平均效率水平。为了量化分析各地区技术效率的空间特征,本文运用全局Moran-I指数来计算1999~2008年间区域技术效率的空间相关性。
在进行空间效应分析时,空间权重矩阵W是衡量区域空间效应的重要变量。与以往运用空间二元毗邻矩阵计算空间结构矩阵不同,本文采用Anselin,Bera[15]空间距离矩阵来分析技术效率的空间溢出效应。为了深入理解空间技术溢出效应与空间距离之间的关系,本文将中国区域空间距离划分为0~750km、0~1500km和全域三个不同的空间范围,并采用式(5)来计算区域空间权重矩阵。
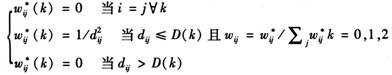 (5)
(5)
其中,Wij*为未标准化空间权重矩阵,Wij是行标准化空间权重矩阵,dij是省会城市i和j之间的列车行驶距离;D(0)=750km,D(1)=1500km,D(2)为所有区域间的空间最大距离。通过计算不同空间权重矩阵可以有效检验空间溢出效应随距离而变化的规律。
