会员登录
会员注册内容提要：以极值统计学为理论基础，研究分区多目标风险模型在银行操作风险计量中的适用性。在已知有限的极值事件概率信息下，确定极值风险函数以评估极值事件引起的损失期望值，从而为操作风险损失配置恰当的经济资本，并通过实例研究验证该方法的可行性。
关键词：操作风险 极值理论 分区多目标风险模型 广义极值分布
作者简介：蔡则祥孙清南京审计学院，南京210029
引言
尽管操作风险是银行与生俱来的“老问题”，然而，对其量化管理却是“新事物”。国内外银行界对操作风险的关注只是近几年的事情。1995年巴林银行的破产倒闭给全球金融机构敲响了警钟：操作风险成为金融机构面临的最大威胁之一，巴塞尔委员会开始重视对操作风险的关注，并于2004年在新资本协议中将其纳入风险资本的计算和监管框架。从国内来看，2005年年初以来，中国银行业先后爆发多起金融大案，其涉案金额之巨、爆发频率之高令银行业内外为之震惊，国内银行业面临的操作风险形势严峻。银监会下发的《关于加强防范操作风险工作力度的通知》，标志着操作风险已纳入监管者和经营者的视野。
银行业操作风险危害巨大。国内外发生的一系列操作风险大案要案告诉我们，操作风险可能会给银行带来灭顶之灾。就国内银行业面临的操作风险形势来看，如果对引发信用风险、导致不良资产的诸多案例进行综合分析就会发现，相当比例的信用风险案件是因为违规操作等操作风险因素引致的。可以说，国内银行业如果出现破产倒闭事件，罪魁祸首可能不是信用风险，也不会是市场风险，而是长期被人们所忽略的操作风险。所以，现在有必要重视和加强对操作风险管理的研究，特别是对操作风险计量分析。
本文通过应用分区目标设定的方法，改进POT(peak-over-thread)极值模型的阈值的确定问题，从而提高估计的精度与稳定性。文章结构安排如下：首先简要介绍巴塞尔新资本协议（Basel Accord Ⅱ）对操作风险(Operational risk)监管的要求及其国内外研究状况，然后阐述极值理论的基础概念、建立分区多目标操作风险模型，最后通过实例对模型进行验证。
一、文献回顾
理论界对操作风险的研究是从定义操作风险开始的，然而至今尚未取得一致意见。1988年9月，巴塞尔银行监管委员会首次发布了《操作风险管理》文件，采用了英国银行家协会(BBA)对操作风险的定义：即由于内部程序、人员、系统的不完善或失误，外部事件造成的直接或间接损失的风险。JP Morgan则将操作风险定义为各公司业务和支持活动中内生的一种风险因素，这类风险表现为各种形式的错误、中断、或停滞，可能导致财务损失或者给公司带来其他方面的损害。还有人认为：操作风险是指在银行内由于顾客、不足的内部控制、系统或控制失败以及不可控制的事件所引起的收入或者现金流的波动，例如银行遭受外部人员的欺诈、内部人员舞弊、机构内的信息系统崩溃导致营业中断、战争灾害等突发事件导致固定资产损失等各种风险。操作风险涵盖的内容非常广泛，对于商业银行而言，几乎包括了市场风险和信用风险以外所有的风险。
在相当长的时期内，操作风险被认为是不能量化的，商业银行对信用风险和市场风险的重视程度远远超过了操作风险。随着金融风险管理技术的进展，目前银行已经能较为准确地对操作风险进行定义、识别、衡量、监管和防范，各种内部模型也不断确立。巴塞尔银行监管委员会也在其发布的巴塞尔新资本协议（Basel Accord Ⅱ）中把操作风险纳入风险量化和监管领域。协议根据损失事件类型把引起损失的操作风险分为七类事件，按照发生损失事件的业务部门分为八类部门，发生损失的原因和发生损失的部门组成了操作风险损失事件信息的二维矩阵。为了适应不同银行的情况，巴塞尔新资本协议设计了基本指标法、标准法和高级法等三种由简到繁的方法计量操作风险。
国内外众多学者和银行从业人员，对银行操作风险管理进行了研究和探讨。David Porter(2003)系统地讨论了审计数据分析、管理文化建设、减少金融犯罪等与防范操作风险的关系；Reirner Kuhn和Peter Neu(200)提出了基于VAR模型的银行操作风险资本金计算方法；Elena Medova(2003)引入了极值理论(Extrem Value Theory, EVT)，并分析了极值理论在操作风险资本配置中的作用。
在国内，田玲、蔡秋杰(2003)对衡量操作风险的五种方法即基本指标法、标准化方法、内部衡量法、损失分布法和极值理论模型进行比较分析；陈学毕、杨辉耀(2003)探讨了POT模型在商业银行操作风险度量中的应用，说明POT模型的优点在于可以准确描述分布尾部的分位数，具有解析的函数形式，计算简便；樊欣、杨晓光(2003)从公开媒体报道中所有可能搜集到的国内商业银行的操作风险损失事件，从损失事件类型、业务部门、四大专业银行、区域分布维度，对操作风险损失事件的频度和幅度进行了定量分析，试图对我国银行业目前面临的操作风险的状况给出一个初步的定量概况归纳；他们还于2004年应用收入模型和证券因子模型对国内两家股份制商业银行的操作风险状况进行了实证分析，结果表明：两个模型在某种程度上都可以反映操作风险的大小，收入模型的度量效果优于证券因子模型。曲绍强、王晓芳(2006)对作为操作风险高级度量法之一的损失分布法（LDA法）中的数据收集、模型选择等问题进行了探讨，并针对我国的情况提出了一些建议。
二、极值统计的理论基础
极值统计学是数理统计学的一个分支，主要是处理一定样本容量的最大值和最小值，可能的最大值与最小值将组成它们各自的母体，因此这些值可用具有各自概率分布的随机变量来模拟。
对于方程(1)，当n变得很大或n→∞时，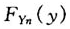
是否具有极限的或渐近的形式，这一问题曾经是早期的统计学者所探讨的课题，并已成为人所共知的统计极值的渐近理论，它使得极值统计学的用途大为增强。
当n很大时，极值的渐近分布趋向收敛于几种极限形式，Gumbel把它们划分为Ⅰ、Ⅱ、Ⅲ型的渐近形式：来自带有指数型衰减尾部的初始分布的极值将渐近地收敛于Ⅰ型极限形式；而对于具有二项式衰减尾部的初始分布，它的极值将收敛于Ⅱ型渐近形式；对于有界的极值，其相应的极值分布将收敛于Ⅲ型渐近形式。
描述极值统计的两个基本要素是Gumbel渐近分布形式与极值参数。在实际应用中，判断初始随机变量的确切分布常常比较困难，但描述极值风险事件后果是极其重要的，而它又是初始随机变量的函数。因此，在初始随机变量的尾部情况不够明确时，必然会带来如何确定其极值分布的极限形式问题，以便确定极值风险的均值和方差。为此，可利用Von Mises准则作为指南。Asbeck在Von Mises收敛准则的基础上推导了初始变量X为极值Ⅰ、Ⅱ、Ⅲ型时，Y=g(X)为Gumbel极值分布形式的条件（见表1）。
表1Y为Gumbel Ⅰ、Ⅱ、Ⅲ型分布条件
注：①表示X应满足Von Mises收敛准则；②[dg(x)/dx]/gx应为X的单调函数。
三、操作风险的模型构建
对操作风险的管理，首先要对风险暴露进行量化。这就要对各类银行业务因操作问题而造成损失的历史资料进行统计分析，以建立风险指标体系，用来表征某类事件或某类业务的操作风险的大小。在这个过程中，如何进行损失数据的收集就成为了其核心的内容。从数据来源看主要分为内部与外源两种。内部数据是指公司内部关于公司所经历的损失事件和损失数量的列表，行业数据主要来源于行业协会收集到的数据，这些协会收集银行的内部损失数据，并在该协会中进行共享公共数据主要是指公开使用的数据。由于缺乏内部数据，如果仅仅使用这些少量的数据对损失频率和损失分布参数进行估计，会产生很大的抽样误差，从而预测的经济资本会随时间发生很大变化，风险预算也就变得非常困难。正因如此，银行需要考虑使用外部数据源来补充内部数据。然而在这个过程中银行并不能简单地将外部数据直接作为内部数据处理，而应当明确一定的程序和方法，对来自其他数据源的外部或内部损失数据进行适当的转换。
正因如此，巴塞尔委员会没有规定操作风险计量和计算监管资本所需的具体方法和统计分布假设。但要求银行必须充分考虑“低概率、高损失”的“尾部”事件。因为不经常发生的操作风险事件一旦发生，可能会给银行带来致命打击，甚至破产，例如英国的巴林银行。实际上，操作风险事件发生频率和损失强度是不一致的。巴塞尔新资本协议中归纳的七类操作风险事件，其发生频率和损失强度可定义如表2。
操作风险发生的频率较低，但可能会引起巨大的损失。利用巴塞尔委员会2002年收集的全球89家银行47269笔损失数据，Moscadelli和Fontnouvelle等人均发现了损失数据的厚尾分布特性。极值理论模型的优势在于它直接处理损失分布的尾部，且没有对损失数据预先假设任何的分布，而是利用数据本身说话，而且对可能超过VaR的操作风险损失给出了预测，因此它更适合对低频高危类型的操作风险事件进行防范。极值理论法中常用的模型有两种，即BMM模型(block maxim model)与POT(peak-overthreshold)模型，BMM模型主要对块最大值(block maxim)建模，POT模型则对观察值中所有超过某一较大阈值的数据进行建模，是实践中最常用的模型。阈值的确定是极值理论分布估计的关键。从理论上讲，阈值应极大，但阈值越大，用来估计尾部分布函数的观察值就越少，估计的波动性也越大，所以需要找到合适的阈值。Asbeck和Haimes提出的分区多目标风险方法(The Partitioned Multi-Objective RiskMethod)很好地解决了上述问题，它是一种基于条件期望值概念的风险量化方法，将期望值的概念推广到生成多个条件期望值函数，与传统的期望值法相比，它给出了一个更完整的风险描述。
表2操作风险事件发生频率和损失强度分类表
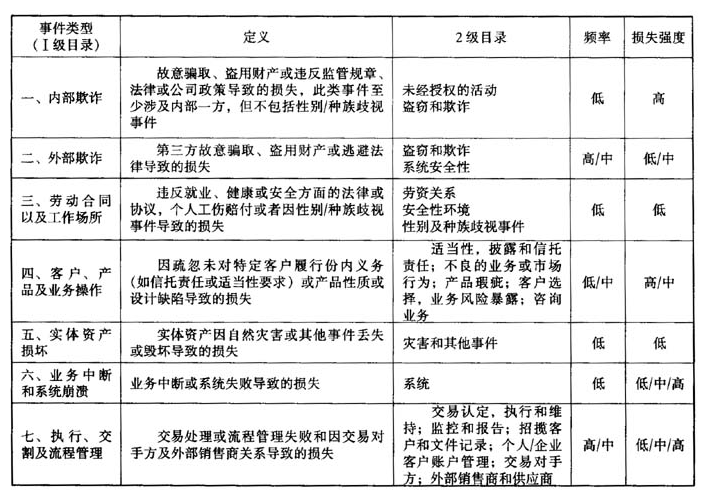
条件期望值函数定义为随机变量在几个划定的概率范围内的期望值，显然条件期望值的大小取决于概率轴的划分，而分区点的选择由银行管理者根据具体操作风险的极值特点主观确定。
四、应用研究
根据上述理论进行应用研究。设X为巴塞尔协议定义某类银行业务内外源总体操作风险损失量，Y为对应某银行的操作风险损失，它们间的关系为Y=g(X)。假定业务量X服从一特定分布，如对数正态，Gumbel分布或Weiball分布等，且存在转换函数g时，随机变量Y的确切分布很容易得出。利用基础数据资料，我们可以运用极大似然估计法和矩法（或有序统计法）确定X的最大样本值的Gumbel极值参数，由于X的确切初始分布仍常难以确定，问题就成为在已知有限的X的概率描述信息及转换函数g下，研究函数Y的极值，以评估稀遇操作风险事件引起的损失期望值。
图2内外源总体操作风险损失和某银行的操作风险损失
因为n=100，由式(12)对得1-α=1%即重现期不小于百年一遇的操作风险引起的损失期望值为10435648（＄），Y的概率密度示意图（见图3），图中阴影部分面积为概率（1-α）。
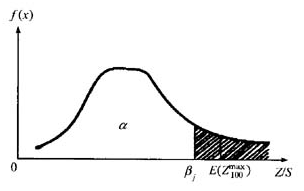
图3风险预期概率密度示意
五、结论
本文首先阐述了极值统计学的基本原理，并利用Von Mises收敛准则作为指南，在初始随机变量概率密度函数的尾部情况不够明确时，判别初始随机变量极值分布的极限形式，再运用某一随机变量与初始变量的函数转换关系，利用表1的判别形式判定某一随机变量的极值分布形式；其次，研究了极值统计与分区多目标风险方法中的极值风险函数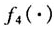
的联系，并概括了极值风险变量为最大值Ⅰ、Ⅱ、Ⅲ型渐近分布时，
的近似计算式。在操作风险评价中，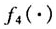
表示重现期大于或等于n年的期望操作风险损失值，它为密切关注操作风险的银行管理者为抵御风设事件准确配置资本金提供有效的理论评估依据。