我国银行间同业拆借利率的动态研究——基于跳跃—扩散—机制转换模型的实证分析

内容提要：针对我国短期利率易受政策影响，波动较大并存在结构变化等特点，构建了跳跃—扩散—机制转换模型，同时考察了银行间7天同业拆借利率的波动、跳跃和结构变化三种效应，发现我国同业拆借利率不仅具有均值回归特性而且还存在明显的跳跃与机制转换，并且该模型比其嵌套的受限模型表现更佳。在高波动状态下利率波动的水平效应和ARCH效应可以忽略；低波动状态下，水平效应可以忽略。另外，跳跃具有聚类效应，高（低）的跳跃概率和高（低）状态概率对应着高（低）利率和较高（低）的波动率，跳跃主要发生在高状态机制下，低状态机制下发生跳跃的可能性很小。
    关键词：同业拆借利率 跳跃 扩散 机制转换 ARCH效应
    作者简介：吴吉林（1979-），男，浙江安吉人，博士，山东大学经济研究院讲师（济南250100）；张二华，上海财经大学经济学院（上海200439）；原鹏飞，国家统计局统计科学研究所（北京100826）。
    0引言
    短期利率是央行执行货币政策的重要传导工具，并且在金融衍生品定价和利率风险管理中发挥核心作用。在研究短期利率的动态模型中，最早提出的是单因子模型如Vasicek、CIR、CKLS以及Ait-Sahalia[1-4]等，它假设短期利率的动态过程完全由漂移项和扩散项决定。虽然这些模型能基本描述短期利率的均值回归和扩散运动，但是仍无法解释市场利率变动的一些更重要经验事实如利率变动的非正态性，尖峰性以及波动的聚类效应（洪永淼和林海[5]）。为了解释这些现象，一些学者提出了许多更为复杂的模型，如Brenner等[6]在扩散项中引入了GARCH效应，Andersen和Lund[7]、Ball和Torous[8]在CKLS模型中引入了随机波动效应。但研究发现引入ARCH、GARCH和随机波动虽能显著提高短期利率的样本内拟合效果，但波动效应持久不衰，甚至随机波动效应还呈爆炸似扩张。正如Lamoureux和Lastrapes[9]、Chapman和Pearson[10]等所证实，信息、政策和异常事件冲击必然会引起利率发生跳跃和结构变化，未考虑跳跃或结构变化会使模型存在误设的可能，从而错误地夸大了波动的持久性。因此，在模型中引入跳跃或机制转换就非常必要。如Cai、Gray[11-12]分别在ARCH、GARCH模型中引入机制转换，Smith、Kalimipalli和Susmel[13-14]在随机波动模型中引入机制转换。他们都发现引入机制转换后模型拟合能力不仅有较大提高，而且波动的持久性也显著下降。Johannes[15]发现跳跃行为在利率的变动中发挥着重要作用，并对利率衍生品定价产生显著影响。另外，Das[16]在单因子ARCH模型中引入了跳跃后发现跳跃因子在刻画美国短期利率中发挥着必不可少的作用，而且在跳跃、扩散基础上再引入机制转换能更进一步改善模型的拟合效果。Benito等[17]欧元隔夜利率的研究证实了包含跳跃、机制转换的单因子模型在样本内拟合与样本外预测的表现都较好。
    相对于国外学者，国内学者对短期利率的研究起步较晚，研究方法主要集中在以下三类：第一类为简单单因子模型，如，吴冲锋[18]等利用单因子Vasicek模型和CIR模型研究了国债回购利率特征，但发现两模型实证结果相差很大。董乐[19]以银行间和交易所的回购利率为研究对象，在Vasicek、CIR、CKLS利率模型基础上，检验了它们的均值回复特征。马晓兰和潘冠中[20]提出了更一般的单因子扩散模型，并考察了7天回购利率的运动特征。基于SNP-EMM法，范龙振[21]比较了多种不同的单因子利率模型能否描述上海证券交易所国债交易的短期利率的变动特征。第二类为单因子基础上的结构变化模型。如，谢赤和吴雄伟[22]回归中使用虚拟变量证实了我国利率存在结构转换。陈晖和谢赤[23]运用Gray提出的机制转换GARCH模型考察了银行间30天同业拆借利率，进一步证实中国利率的确存在机制转换，且利率波动较小时存在均值回归现象，而在利率波动较大时不存在均值回归。刘金全和郑挺国[24]在CKLS模型中引入机制转换研究了我国同业拆借市场的月度加权利率，发现漂移项和扩散项都呈现非线性，其中漂移函数表现为强烈的随机游走过程或均值回归过程，而扩散项表现为低波动状态或高波动状态。吴吉林和陶旺升[25]在Ait-Sahalia[4]非线性扩散模型基础上引入了随机波动和机制转换，发现我国银行7天同业拆借利率存在明显的非线性、机制转换和波动的水平效应，而且引入机制转换后波动的持久性显著下降。第三类为单因子基础上的跳跃模型。如，林海和郑振龙[26]使用纯跳跃模型对中国政府利率变动行为进行了模拟和分析。陈晖和谢赤[27]比较了Jump-ARCH模型与其嵌套模型间的拟合能力，发现Jump-ARCH模型在刻画我国短期利率的动态特征上是最优的，并且跳跃还存在周内效应。张金清和周茂彬[28]宏观信息冲击视角出发，通过在Vasicek模型中引入与宏观经济变量相关的跳跃成分发现，我国短期利率不仅存在均值回复和扩散行为，还存在显著的跳跃行为，并且跳跃强度存在显著的正向水平效应和宏观经济效应。另外，Hong等[29]利用GARCH模型、马尔可夫机制转换模型以及跳跃—扩散模型等首次较系统地对我国短期利率研究结果证实，在单因子扩散模型中考虑波动、跳跃或机制转换效应会大大地改善短期利率模型的表现，并降低模型设定误差。同时还发现IPO新股发行以及宏观信息和政策冲击对我国利率运动特征产生显著影响。
    虽然在单因子模型中引入跳跃或机制转换等效应能大大地改善模型的表现，但正如洪永淼和林海[5]所指出，没有一个简单的利率模型可以准确描述中国短期利率特征。与发达国家利率市场相比，我国短期利率市场更易受信息、政策冲击影响，利率波动较大，并可能存在较多的跳跃和结构变化。忽略波动、跳跃和机制转换中的任何一种效应都将可能引致模型的误设。国外学者Benito等[17]对欧洲短期利率的研究中发现，同时引入ARCH、机制转换和跳跃将明显改善模型的拟合效果。而到目前为止，我国学者还没有在统一框架内同时考虑这三种可能的效应，他们至多只在波动基础上考虑跳跃效应或者机制转换效应。作为洪永淼和林海[5]以及吴吉林和陶旺升[25]研究工作的继续，试图首次在统一框架内通过同时考察这三种效应来研究我国短期利率的动态特征，然后主要比较该模型与任何只考虑一种或两种效应的模型间的优劣。相对于单一机制扩散—跳跃模型，引入机制机制转换后，由于假设高低状态下存在不同均值回归速度和跳跃副度，这使得我们更容易发现单一机制不能揭示的短期利率特征；相对于不考虑跳跃的扩散—机制转换模型，在高低两状态下引入不同幅度和强度的跳跃因素，将有助于更好地了解短期利率波动的聚类特征。至少从检验结果来看，考虑三种效应的跳跃—扩散—机制转换模型比只考虑一种或两种效应的其他模型表现要好。
    1模型构建与实证方法
    1.17天同业拆借利率数据特征分析
    选取我国银行间7天同业拆借市场月度加权平均利率作为短期利率数据，样本范围从1996年1月到2008年11月，共计155个观察值。所有数据来源于锐思金融研究数据库，并经过等价的年度复利化处理。图1给出了7天同业拆借利率的水平和差分图。图1（a）显示7天同业拆借月度加权利率从1996年初的9%左右逐渐下降到2005年10月的1.5%左右，然后又逐步略有上升。从图1（b）可以看出两次较大的波动分别是1997年底到1999年中期以及2006年初到2008年11月，并且7天拆借利率变动具有聚类效应，利率越高，波动越强。
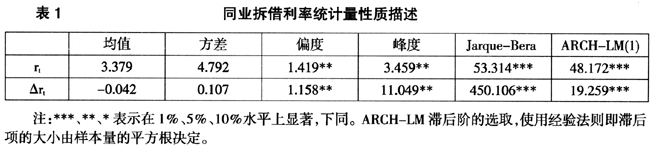
    表1给出了7天同业拆借利率的水平值和一阶差分值统计量性质。其偏度和峰度在5%的水平上都显著不等于O，因此7天拆借利率具有明显的尖峰性质。Jarque-Bera统计量在1%的水平上拒绝了水平值和差分值服从正态分布的假设。并且ARCH-LM检验支持同业拆借利率的水平值和差分值分别在1%和10%的显著水平上存在自回归条件异方差即ARCH效应。由图1和表1分析可知，我国银行间7天拆借利率具有尖峰、非正态性质，并且波动较大，可能存在跳跃和结构变化。因此，在本文中同时考察波动、跳跃和机制转换效应具有合理性。
    
    
    1.2跳跃—扩散—机制转换模型构建
    
    
    2实证分析及结果
    
    
    
    但单一机制模型不能反映经济的结构性变化，而且假定无论是在高利率下还是低利率下，均值回顾速度、波动的ARCH效应和水平效应都相同，所有这些假定都未必能够反映我国同业拆借市场利率的真正特点。因此，相对于模型1、模型2，模型3、模型4、模型5由于引入两状态的机制转换增加了模型的灵活性，而且在不同的机制下设定不同的均值回归速度、不同波动的ARCH效应、水平效应，这些都能更清晰地揭示同业拆借市场利率的特征。由于在CKLS模型中引入跳跃和机制转换后，模型5相对于模型2、模型3将存在不可识别的噪声参数，普通的似然比检验失去有效性，而Vuong[31]提出的广义似然比检验可以用来判定存在噪声参数的任何嵌套或非嵌套两模型间在解释短期利率特征中哪个更具有竞争力，其统计量为
    
    
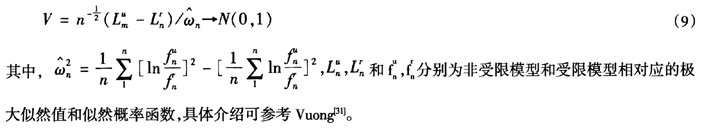
    通过模型5与模型1、模型2、模型3、模型4比较可知，同时考虑三种效应的跳跃—扩散—机制转换模型比任何只考虑两种效应的其他模型表现要好。在引入跳跃和机制转换后，高波动概率机制下的水平效应和ARCH效应都消失，这意味着高波动机制下的波动是由跳跃和结构变化引起的；而在低波动机制下，虽然波动的水平效应也消失，但仍旧在5%水平上存在ARCH效应，所以ARCH效应不能忽略。以上说明在刻画我国银行间7天同业拆借利率时，ARCH、跳跃和机制转换等三种效应是不可缺少的。
    图2（a）中给出了利率变动的标准残差绝对值以及从模型5中获得的利率变动标准差，并用其表示同业拆借利率变动的波动率，其中，原始标准残差来自于使用White[32]异方差一致协方差矩阵估计量对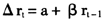的估计，而模型5的标准差来自于式（9）中方差的平方根。图中显示相对于原始数据得到的残差波动图，引入了跳跃和机制转换后，模型5获得的标准差有较大下降，我们可以断定跳跃、机制转换的引入由于能更加准确的刻画信息、政策冲击而引起的波动变化，许多“貌似”较大的波动应归因于跳跃因素和结构变化的存在。
    
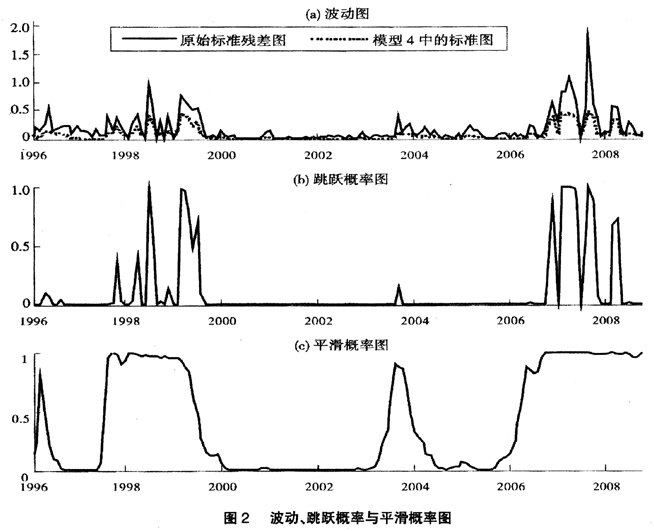
    图2（b）、图2（c）分别给出了模型5的跳跃概率和高波动状态下的平滑概率Pr[St=0|IT]图。图中显示，与波动的聚类效应一样，跳跃也具有聚类效应，较大的跳跃概率紧跟着较大跳跃概率的可能性较大，而较小的跳跃概率紧跟着较小跳跃概率的可能性也较大。图2（b）中较大的跳跃概率对应着图2（c）中平滑概率的高状态概率，而且也对应着图2（a）中较大的波动率。这表明跳跃主要发生在高状态机制下。在高状态机制下，利率的波动幅度较大，引起跳跃发生的可能性也较大；而在低状态机制下，利率的变化较小，其发生跳跃的概率也较小。第一个较大跳跃概率区和高状态概率对应于1997年中期到1999年中期的亚洲金融危机和我国货币改革（由直接调控转向间接调控）。在亚洲金融危机期间，为了确保我国金融市场的稳定性，央行在1997年5月到1999年6月的2年时间内连续6次下调人民币利率，导致银行间同业拆借利率跳跃性变化，并在1999年下半年7天拆借利率出现结构性变化，进入低状态概率，同时跳跃强度也进入较小的平稳区，这段时间一直持续到2006年年初，但其间也存在持续时间较短的机制转换如在2004年前的几个月内。但总体来讲，这段时间内，7天拆借利率波动相对平稳，央行共2次调整存款准备金，3次调整利率。从2006年初到2008年11月7天拆借利率波动增大，又进入了高机制概率，我国在这期间内经历了货币政策的调整（从“稳健”转向“适度从紧”）以及2007年开始的全球次贷危机，在这段时间内央行曾21次调整存款准备金和11次调整利率。
    3结束语
    通过在单因子模型中引入ARCH、跳跃和机制转换，对我国银行间7天同业拆借利率进行了考察。研究结果发现：第一，波动、跳跃和机制转换效应在刻画我国7天同业拆借利率中都发挥着必不可少的作用，跳跃—扩散—机制转换模型比任何只考虑一种、两种效应的模型表现更佳。第二，我国同业拆借利率不仅存在明显的均值回归效应，而且存在跳跃与机制转换。两次较大的跳跃区和机制转换分别对应着1997年中期到1999年中期的亚洲金融危机和我国货币改革以及2006年初到2008年11月的我国货币政策的调整和2007年开始的次贷危机。第三，跳跃和机制转换在解释利率的波动率中发挥着重要的作用。在高波动状态下，ARCH效应和水平效应都可以忽略；而在低波动状态下，由于ARCH效应的存在，水平效应可以忽略。第四，跳跃具有聚类效应，较大的跳跃概率紧跟着较大跳跃概率的可能性较大，而较小的跳跃概率紧跟着较小跳跃概率的可能性也较大。另外，平滑概率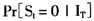的高状态概率和高的跳跃概率对应着高利率和较高的波动率，而低状态概率和低的跳跃概率对应着低利率和低的波动率，跳跃主要发生在高状态机制下，而低状态机制下发生跳跃的概率几乎为零。
    注释：
    ①ARCH模型和GARCH模型都能描述波动效应，而且ARCH模型也是GARCH模型的一种特殊形式。使用GARCH模型和ARCH模型对我们的实证结果不产生影响，而且在既考虑跳跃又考虑机制转换的模型中，GARCH的设定将涉及状态路径相依和跳跃概率，这使得模型的估计较繁琐。为了模型的简洁，使用ARCH模型。
    ②其值位于0～100，值越小，机制越明显。当RCM=0时，这时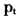=1或0，表明存在非常明显的机制转换，而当RCM=100时，这时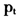=0.5，表明不确定是否存在机制转换。本质上，RCM值为样本的方差估计值。
    参考文献：
    [1]Vasicek O. An equilibrium characterization of the term structure[J]. Journal of Financial Economics, 1977, 5(2): 177-188.
    [2]Cox J C, Ingersoll J E, Ross S A. A new theory of the term structure of interest rates[J]. Econometrica, 1985, 53(2): 385-407.
    [3]Chan K, Karolyi G, Longstaff F, et al. An empirical comparison of alternative models of the short-term interest rate[J]. Journal of Finance, 1992, 47(3): 1209-1227.
    [4]Ait-Sahalia Y. Testing continuous-time models of the spot interest rate[J]. Review of Financial Studies, 1996, 9(2): 385-426.
    [5]洪永淼，林海.中国市场利率动态研究——基于短期国债回购利率的实证分析[J].经济学(季刊)，2006，5(2)：511-532.
    Hong Yongmiao, Lin Hai. Performance of discrete-time spot rate models in China: An empirical test on Chinese Repo Rates[J]. China Economic Quarterly, 2006, 5(2): 511-532.(in Chinese)
    [6]Brenner R, Harjes R, Kroner K. Another look at models of the short-term interest rate[J]. Journal of Financial and Quantitative Analysis, 1996, 31(1):85-107.
    [7]Anderson T, Lund J. Estimating continuous time stochastic volatility models of the short-term interest rates[J]. Journal of Econometrics, 1997, 77(2): 343-377.
    [8]Ball C, Torous W. The stochastic volatility of short-term interest rates: Some international evidence[J]. Journal of Finance, 1999, 54(6): 2339-2359.
    [9]Lamoureux C, Lastrapes W. Persistence in variance, structural change and the GARCH model[J]. Journal of Business & Economic Statistics, 1990, 8(2): 225-234.
    [10]Chapman D, Pearson N. Recent advances in estimating term-structure models[J]. Financial Analysts Journal, 2001, 57:(4), 77-95.
    [11]Cai J. A Markov model of switching-regime ARCH[J]. Journal of Business & Economic Statistics, 1994, 12(3): 309-316.
    [12]Gray S. Modeling the conditional distribution of interest rates as a regime-switching process[J]. Journal of Financial Economics, 1996, 42(1): 27-62.
    [13]Smith D R. Markov-switching and stochastic volatility diffusion models of short-term interest rates[J]. Journal of Business and Economic Statistics, 2002, 20(2): 183-197.
    [14]Kalimipalli M, Susmel R. Regime-switching stochastic volatility and short-term interest rates[J]. Journal of Empirical Finance, 2002, 11(3): 309-329.
    [15]Johannes M. The statistical and economic role of jumps in continuous time interest rate models[J]. Journal of Finance, 2004, 59(1): 227-260.
    [16]Das S. The surprise element: Jumps in interest rates[J]. Journal of Econometrics, 2002, 106(1): 27-65.
    [17]Benito F, Leon A, Nave J. Modeling the Euro overnight rate[J]. Journal of Empirical Finance, 2007, 14: 756-782.
    [18]吴冲锋，王海成，吴文锋.金融工程研究[M].上海：上海交通大学出版社，2000：37-38.
    Wu Chongfeng, Wang Haicheng, Wu Wenfeng. The Research on Financial Engineering[M]. Shanghai: Shanghai Jiaotong University Press, 2000: 37-38.(in Chinese)
    [19]董乐.我国短期利率均值回复假设的实证研究[J].数量经济技术经济研究，2006,23(11)：151-160.
    Dong Le. An empirical test of mean-reversion hypothesis of short-term interest rate in China[J]. Quantitative and Technical Economics, 2006, 23(11): 151-160.(in Chinese)
    [20]马晓兰，潘冠中单因子利率期限结构模型的广义矩估计及对中国货币市场的实证检验[J].数量经济技术经济研究，2006,23(1)：107-116.
    Ma Xiaolan, Pan Guanzhong. GMM estimation for single-factor term structure of interest rate models and the empirical test of Chinese money market[J]. Quantitative and Technical Economies, 2006, 23(1): 107-116.(in Chinese)
    [21]范龙振.短期利率模型在上交所债券市场上的实证分析[J].管理科学学报，2007,10(2)：80-89.
    Fan Longzhen. Empirical analysis of short interest rate models with half-year interest rate in the Shanghai Stock Exchange[J]. Journal of Management Sciences in China, 2007, 10(2): 80-89.(in Chinese)
    [22]谢赤，吴雄伟.一个基于水平模型的利率结构转换模型[J].系统工程，2002,20(1)：20-23.
    Xie Chi, Wu Xiongwei. The regime switching model based on the level model[J].System Engineering, 2003, 20(1):20-23.(in Chinese)
    [23]陈晖，谢赤.中国银行间同业拆借市场利率结构转换研究[J].管理科学，2004,17(4)：65-70.
    Chen Hui, Xie Chi. An analysis on regime-switching of interest rate in the inter-bank market of China[J]. Management Sciences in China, 2004, 17(4): 65-70.(in Chinese)
    [24]刘金全，郑挺国.利率期限结构的马尔科夫区制转移模型与实证分析[J].经济研究，2006，41(11)：82-91.
    Liu Jinquan, Zheng Tingguo. Markov regime switching model and empirical analysis of the term structure of interest rates[J]. Economic Research Journal, 2006,41(11): 82-91.(in Chinese)
    [25]吴吉林，陶旺升.基于机制转换与随机波动的我国短期利率研究[J].中国管理科学，2009,17(3)：40-46.
    Wu Jilin, Tao Wangsheng. Markov-regime switching and stochastic volatility model of short-term interest rate in China[J]. Chinese Journal of Management Science. 2009, 17(3):40-46.(in Chinese)
    [26]林海，郑振龙.中国利率动态模型研究[J].财经问题研究，2005,262(9)：45-49.
    Lin Hai, Zheng Zhenlong. Dynamic behavior of interest rates in China[J]. Research on Financial and Economic Issues, 2005, 262(9): 45-49.(in Chinese)
    [27]陈晖，谢赤.包含Jump-Arch过程的利率模型及其应用[J].管理科学学报，2008，11(2)：80-90.
    Chen Hui, Xie Chi. Diffusion model including the jump-arch process and its application[J]. Journal of Management Sciences in China, 2008, 11(2):80-90.(in Chinese)
    [28]张金清，周茂彬.中国短期利率跳跃行为的实证研究[J].统计研究，2008,25(1)：59-64.
    Zhang Jinqing, Zhou Maobin. Empirical research on the jump behavior of Chinese short rate[J]. Journal of Statistical Research, 2008, 25(1): 59-64.(in Chinese)
    [29]Hong Y, Lin H, Wang S Y. Modeling the dynamics of Chinese spot interest rates[J]. Journal of Banking and Finance, 2010, 34(6): 1047-1061.
    [30]Ang A, Bekaert G. Regime switches in interest rates[J]. Journal of Business and Economic Statistics, 2002, 20(2): 163-182.
    [31]Vuong Q. Likelihood ratio tests for model selection and non-nested hypotheses[J]. Econometrica, 1989, 57(2): 307-333.
    [32]White H. A heteroskedasticity-consistent covariance matrix estimator and a direct test for heteroskedasticity[J]. Econometrica, 1980, 48(4):817-838.