面板数据非线性阈值协整的检验方法

内容提要：非线性阈值协整是线性协整的后续发展。本文使用两机制TR模型对Westerlund和Edgerton（2005）的面板数据协整向量结构突变模型进行扩展，提出截距项具有阈值效应、截距项和斜率系数都具有阈值效应的面板数据非线性阈值协整模型。在此基础上，本文进而分别构造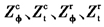统计量检验阈值协整，并对上述统计量的极限分布进行了数学推导，发现它们都收敛于随机泛函。仿真实验结果表明，有限样本下上述检验统计量具有较小的水平扭曲和较高的检验势。
    关键词：面板数据 非线性 阈值协整 检验
    作者简介：欧阳志刚，华东交通大学经济管理学院。
    引言
    自Engle和Granger（1987）基于单位根数据提出协整理论后，协整分析方法在时间序列数据的应用研究中逐步占据主导地位。许多经济学家使用协整方法研究了经济变量之间的长期均衡和短期动态调节。然而，标准协整理论要求经济变量的长期均衡和短期调节为线性，但大量的经济理论和经济实践都表明，线性假定过于严格（Escribano，2004），具有单位根特征的经济变量间的关系也许是非线性的。当面对经济变量的非线性关系时仍然使用线性方法进行研究，得出的结论可能是错误的（Gonzalo等，2006）。因此，基于方法论的进步和实证研究的需要，近期许多文献在非平稳数据框架内引入非线性，并由此形成计量经济学的一个前沿热点领域。
    使用非线性对线性协整的改进包括两个方面：协整关系的非线性和短期调节的非线性①。在协整关系的非线性文献中，Chang等（2001）发现在非平稳非线性回归模型中，非线性最小二乘法将产生无效估计量和不可靠的假设检验。Chang和Park（2003）在变量为非平稳单位根过程的条件下，使用STR构造回归模型，发现对模型的非线性最小二乘估计会导致有偏的结果，并且其极限分布依赖未知参数。针对这一结果，他们借鉴Phillips和Hansen（1990）、Park（1992）的方法，校正了非线性最小二乘法，得到极限分布为标准分布的估计量。Saikkonen和Choi（2004）在解释变量内生性的非线性协整框架内提出使用非线性动态最小二乘法估计协整向量。欧阳志刚（2010）将Saikkonen和Choi（2004）的估计方法扩展为完全修正的最小二乘法，并提出构造LM统计量检验协整关系的非线性。Choi和Saikkonen（2005）进一步在解释变量内生的假定下，基于非线性动态最小二乘的残差分块构造KPSS统计量检验阈值协整的方法。Gonzalo和Pitarakis（2006）使用TR模型研究协整向量的阈值机制转移，并分别在解释变量为外生性和内生性条件下，构造LM统计量检验协整向量的非线性阈值效应。
    容易看出，上述文献所提出的非线性协整的估计与检验统计量的分布都是基于极限分布得到的。在有限样本，尤其是小样本下，估计和检验统计量的分布相对于极限分布会产生水平扭曲并导致较低的检验势，因此，其实用可靠性取决于有限样本性质。而在实际应用中，由于时间序列数据的采集通常在时间跨度上受到限制，所以实证研究通常很难得到足够大的样本容量，从而降低了研究结论的可靠性。因此，增加样本容量是提高检验结果准确性的有效方法之一。方便而有效地增加样本容量的方法是将时间序列数据扩展为面板数据，面板数据不仅增加了样本容量，而且提供了更多的相关经济信息，从而有可能改进基于时间系列数据的非线性协整估计与检验统计量的有限样本性质。因此，如何将非线性阈值协整扩展至面板数据就成为当前面临的前沿课题。由于方法论的复杂性，国内、外文献中还没有发现在这一前沿领域的较为成熟的研究成果②。本文将Westerlund和Edgerton（2005）基于协整向量结构突变的面板协整检验方法扩展为协整向量阈值机制转移的面板协整模型，并对上述扩展的检验统计量的极限分布进行相关的数学证明，同时利用蒙特卡罗仿真实验分析其有限样本性质。
    一、面板数据的阈值协整检验方法
    1.截距项含阈值效应的面板数据阈值协整模型
    （1）模型的设定。参照Westlerlund和Edgerton（2005）、Gonzalo和Pitarakis（2006）的模型设定和数据生成过程，面板数据阈值协整模型设定如下：
    
    
    
    
    
    
    
    
    
    
    
    
    
    
    2.截距项和斜率系数含阈值效应的面板数据阈值协整模型
    模型（1）仅允许单个横截面的截距具有阈值效应，可以方便地把模型（1）扩展至截距和斜率系数同时具有阈值机制转移的情形：
    
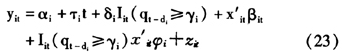
    模型（23）中变量和参数的含义同前，特别地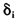，和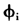分别表述了机制转移发生前后截距项和斜率系数的变化。如前所述，检验阈值面板协整的LM统计量可以从下在的辅助回归导出：
    
    
    二、面板阈值协整检验统计量的有限样本性质
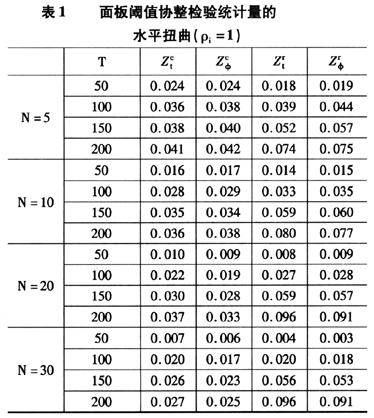
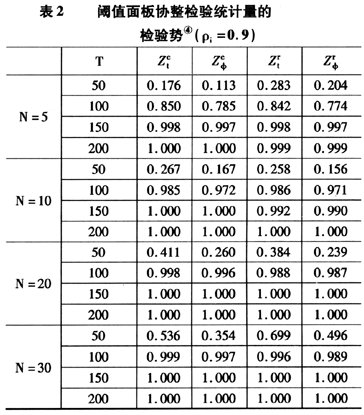
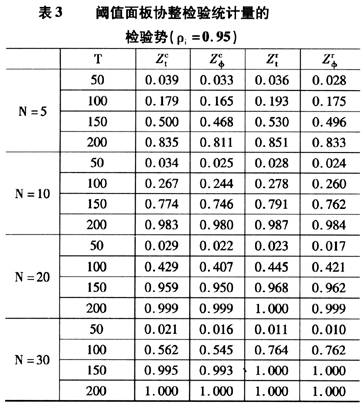
    前述仅分析了面板阈值协整检验统计量的极限分布，在实际应用中，大样本数据往往难以得到，在有限样本下，上述面板阈值协整检验统计量是否有优良的统计性质？这一点对其应用研究特别重要。本文使用蒙特卡罗仿真实验对此进行分析。仿真实验中的数据生成过程如下：
    
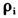    参数的大小确定了原假设和备择假设，即=1对应没有协整关系的原假设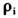，<1对应存在协整关系的备择假设。为方便计算，类似于Westerlund和Edgerton（2005），在备择假设下，设定所有横截面的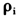=p<1。进一步，为避免数据生成过程中的初始值效应，每个横截面成生T+50个数据，其中前50个数据被剔除掉。
    
    
    
    
    
    三、结论
    标准的协整理论由于假定协整向量和误差校正模型为线性而使其不能分析现实中经济变量之间的非线性关系，对此进行扩展的方向之一就是在标准协整框架内引入非线性阈值机制转移模型。本文在现有基于时间序列数据的非线性阈值协整模型的基础上，将其扩展为基于面板数据的非线性阈值协整模型。针对扩展的模型，本文借鉴Westerlund和Edgerton（2005）的方法分别构建了截距项含阈值效应、截距项和斜率系数都含阈值效应的面板数据阈值协整检验统计量，并推导了上述检验统计量的极限分布。仿真实验结果说明，本文构造的检验统计量具有较小的水平扭曲和较高的检验势，因此，本文提出的方法具有较好的应用价值。
    注释：
    ①限于篇幅，这里没有讨论短期调节非线性的文献。
    ②现有的非线性面板数据文献都是基于平稳数据，如Fok等（2005）、Kapetanios等（2010）。
    ③定理2的证明类似定理I，限于篇幅，此处略去，备索。
    ④自回归系数取值越小，表示越远离原假设。本文的仿真实验发现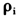，取值越小检验统计量的具有更高的检验势。限于篇幅，本文仅报告了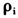取值较大时仿真结果。
    参考文献：
    [1]Ahn S. K., 1993, Some Tests for Unit Roots in Autoregressive-Integrated-Moving Average with Deterministic Trends[J], Journal of Biometrica, 80(4), 855～868.
    [2]Andrews D. W. K., 1993, Tests for Parameter Instability and Structural Change with Unknown Change Point[J], Econometrica, 61(4), 821～856.
    [3]Bai J., 1997, Estimating Multiple Breaks One at a Time[J], Journal of Econometric Theory, 13(3), 315～352.
    [4]Bai J., Perron P., 1998, Estimating and Testing Linear Models with Multiple Structural Changes[J], Econometrica, 66(1), 47～78.
    [5]Chang Y., Park J. Y., Phillips P. C. B., 2001, Nonlinear Econometric Models with Cointegrated and Deterministically Trending Regressors[J], Econometrics Journal, 4(1), 1～36.
    [6]Chang Y., Park J. Y., 2003, Index Models with Integrated Time Series[J], Journal of Econometrics, 114(1), 73～106.
    [7]Choi I., Saikkonen P., 2004, Testing Linearity in Cointegrating Smooth Transition Regressions[J], Journal of Econometrics, 7(2), 341～365.
    [8]Engle R. F., Grangle C. W. J., 1987, Co-integration and Error Correction: Representation, Estimation and Testing[J], Econometrica, 55(4), 251～276.
    [9]Escribano A., 2004, Nonlinear Error-Correction: The Case of Money Demand in the United Kingdom(1878～2000)[J], Macroeconomic Dynamics, 8(1), 76～116.
    [10]Fok D., Dijk D. V., Franses P. H., 2004, AMultiLevel Panel Smooth Transition Autoregression for US Sectorad Production[J], Journal of Applied Econometrics, 11(8), 811～827.
    [11]Gonzalo J., Pitarakis Jean-Yves, 2006, Threshold Effects in Cointegrating Relationships[J], Oxford Bulletin of Economics and Statistics, 68(12), 813～833.
    [12]Kapetanios G., Mitchell J., Shin Y., 2010, A Nonlinear Panel Data Model of Cross-sectional Dependence[R], Queen Mary, University of London, School of Economics and Finance in Its Series Working Papers with Number 673.
    [13]Park J. Y., 1992, Canonical Cointegrating Regressions[J], Econometrica, 60(1), 119～143.
    [14]Phillips P. C. B., Hansen B.E. 1990,Statistical lnference in Instrumental Variables Regression with I(1)Processes[J], Review of Economic Studies, 57(1), 99～125.
    [15]Phillips P. C. B., Loretan M., 1991, Estimating Long Run Economic Equilibria[J], Review of Economic Stdies, 58(3), 407～436.
    [16]Saikkonen P., Choi I., 2004, Cointegrating Smooth Transition Regressions[J], Econometric Theory, 20(2), 301～340.
    [17]Schmidt P., Phillips P. C. B., 1992, LM Tests fora Unit Root in the Presence of Deterministic Treats[J], Oxford Bulletin of Economics and Statistics, 54(3), 257～287.
    [18]欧阳志刚：《协整平滑转移回归中的线性检验——基于完全修正最小二乘法的扩展》[J]，《统计研究》2010年第3期。