面板数据计量模型适应性的比较研究（二）

虽然理论上在大样本的情况下(N→∞)完全可以采用Arellano估计量来代替Kiefer估计量，但是并不能确保在小样本的情况下也可以这样做，因为小样本下两种估计量的精确度是不同的。为了对其进行比较，本文通过固定T，针对不同数目的N进行了模拟研究。
    在不考虑序列相关的情况下，本文模拟了一组面板数据，并且估计了β和β的方差。通过模拟多次，就可以得到一系列其估计值，这样一来就可以计算出真实的β方差和β方差估计的平均值。在这里，首先加入了固定个体效应。在不同的模拟中，固定T=10，改变个体的数目，从10增加到250。模拟5000次的结果如表2。（以下模拟实验均是来自5000次蒙特卡洛模拟的结果，均采用MATLAB完成。模拟中设定数据真实的斜率β=1，由于无论在存在个体效应或者时间效应时OLS方法的β估计量都是无偏的，通过5 000次模拟可以得到5000个β值，并可以计算出β的方差，这是该估计值的真实的方差。）
    表2不同个体数情况下各种方法的估计结果（不存在序列相关）
    
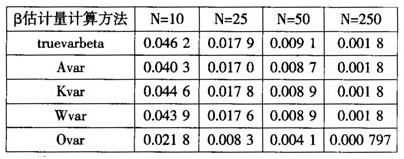
    注：T=10.
    表2中，truevarheta表示真实的β方差，Avar表示基于Arellano估计量计算的β方差的平均值，Kvar表示基于Kiefer估计量计算的β方差平均值，Wvar表示基于White⑤估计量计算的β方差平均值，Ovar表示基于OLS估计量计算的β方差平均值.可以看出，直接用OLS估计明显低估了β的真实方差，在N=10的情况下，OLS估计的β方差仅仅是真实值的47.19%(0.021 8/0.046 2)，随着N的增加，OLS估计量与真实值的比值分别为46.37%、45.05%和44.27%，偏差有所增加，但增加幅度并不大.同时，在样本较小的情况下(N=10)，Arellano估计量与真实方差还是有较大差异的，偏差为12.77%((0.0462-0.040 3)/0.0462)，而Kiefer估计量的偏差仅为3.46%((0.046 2-0.044 6)/0.046 2)，White估计量的偏差为4.98%((0.0462-0.043 9)/0.0462)，这表明在不存在序列相关和小样本的情况下，Kiefer估计量和White估计量的计算结果都比Arellano估计量的精确度高.然而，随着样本规模的逐渐增大，Arellano估计量与真实值之间的偏差逐渐缩小，在本文的模拟实验中，只要N足够大(N≥250)，这几种估计量之间的差异就可以忽略不计。
    由于许多论文在实证过程中往往更关注异方差的情况，而忽略了序列相关这一问题，因此，按照上面的数据结构，本文加上序列相关，重复进行了模拟实验，以期能够得到上述几种估计方法在不同情况下的比较结果，模拟结果见表3.
    表3不同个体数情况下各种方法的估计结果（存在序列相关）
    
    P表示的自相关系数。当P=0.3时，表示的一阶自相关系数为0.3，的一阶自相关系数亦为0.3.表格中第1行数据表示真实的β方差，第2行数据表示基于Arellano方法估计的β方差，第3行数据表示基于Kiefer方法估计的β方差，第4行数据表示基于White方法估计的β方差，第5行数据表示OLS估计的β方差。
    模拟结果表明，加入序列相关后的模拟结果与没有序列相关的情况有着很大的不同。对比N=10的情况可以看出，当序列自相关系数分别为0.3、0.5和0.8时，Arellano估计量、Kiefer估计量和White估计量的偏差分别为9.86%、1%、14.14%；25.70%、9.98%、48.60%；15.30%、5.22%、55.22%.显然，在存在序列相关的小样本情况下，Kiefer估计量要显著优于Arellano估计量和White估计量.White估计量严重偏离了真实值，无论在小样本还是大样本下均如此。在N=250时，Arellano估计量和Kiefer估计量与真实值的偏差分别为0、0(P=0.3)；2.66%、1.90%(P=0.5)；9.09%、0(P=0.8)。这表明在大样本下，Arellano估计量与Kiefer估计量的差异已经很小，这与上面不存在序列相关的模拟结果是一致的。
    为了更形象表示上述结果，进一步给出了上述结果的图表形式，以便能够一目了然小样本情况下各种估计方法的精确情况。
    
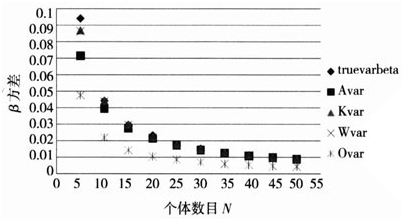
    图2不同个体数情况下各种指数的估计结果（不存在序列相关）
    
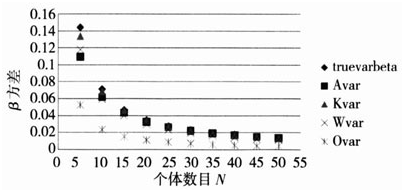
    图3不同个体数情况下各种指数的估计结果（序列相关系数0.3）
    
    图4不同个体数情况下各种指数的估计结果（序列相关系数0.5）
    
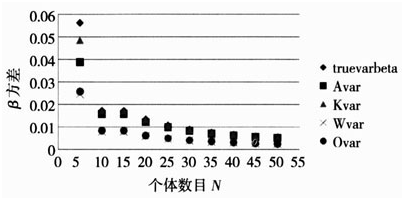
    图5不同个体数情况下各种指数的估计结果（序列相关系数0.8）
    1.1.2Fama-MacBeth误差估计
    现有文献中常见的另外一种估计回归系数和标准误差的方法是Fama-MacBeth方法。该方法的具体运用可表述为研究者首先对面板数据的每一时期的数据进行回归，一共回归了次得到T个β（T代表时期），最后得到Fama-MacBeth的β估计值
    
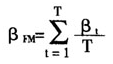
    而该估计值的方差则用下式进行计算
    
    用上文的数据结构，模拟检验了Fama-Macbeth方法的结果，如表4。
    表4只存在固定个体效应的Fama-MacBeth方差估计
    
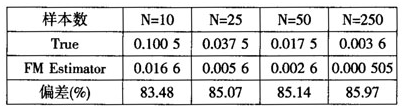
    从上面模拟结果可以看出，当只存在固定个体效应时，Fama-Macbeth方法估计的β方差与真实值之间存在着较大差异，差异甚至大于OLS估计方法（见表1）。在N=10的情况下，OLS的偏差为52.81%，而Fama-Macbeth方法的偏差达到了83.48%，这表明Fama-Macbeth方法并不适合只存在固定个体效应的估计。
    1.2只存在固定时间效应
    与只存在个体效应类似，可假设
    
    1.2.1固定时间效应模型的估计系数
    在只存在时间效应情况下，β系数及其方差的估计与只存在固定个体效应情况下的估计方法类似，在公式的推导过程中，只需将相应的下标i替换为t。为了考察小样本情况下的适用性，本文同样做了模拟。结果显示，当只有10年的数据时，FE模型估计系数产生了一定的偏差。这与本文之前在只存在固定个体效应中的小样本情况下的估计结果是一致的。但是，如果固定N，增加T，随着样本数的增加，FE模型估计将会逐渐产生无偏的结果（与只存在个体效应类似，限于篇幅结果未列出）。从而有理由相信，随着样本数的增加，估计β标准差能够依概率收敛于真实。本文的模拟结果显示，250个样本就足够产生无偏的β标准差估计，而10个样本则显得太少。
    1.2.2Fama-MacBeth误差估计
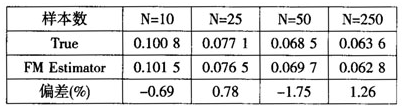
    与上面只存在固定个体效应的模拟结果不同，当只存在时间效应时，Fama-MacBeth方法显示出非常好的效果。固定T=250，不断改变N的模拟结果如表5⑥：
    表5只存在时间效应的Fama-MacBeth方差估计（固定T=250）
    
    既然小样本情况下Fama-MacBeth方法都能产生较好的结果，那么在大样本下情况如何呢？通过固定N=10，不断增加样本数T进行模拟实验，也得到了较好的结果，见表6。
    表6只存在时间效应的Fama-MacBeth方差估计（固定N=10）
    
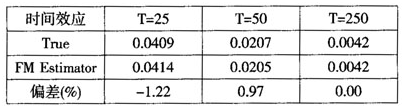
    注：N=10。
    模拟结果表明，无论样本数大小(T)，在只存在时间效应的情况下，Fama-MacBeth方法都能产生较好的估计结果。

（未完待续）