面板数据计量模型适应性的比较研究（三）

1.3同时存在个体效应和时间效应
    1.3.1固定效应模型的估计系数
    以上模拟主要考虑了小样本的情况，因为实际中有些面板数据样本很小，比如公司数目只有几十个，或者更少。根据上面的模拟，可以发现一些有趣的现象，尽管聚类回归方法调整贝塔标准差是有偏的，但是偏离的程度很小，事实上，在聚类数目为50时，偏离的程度只有4.40%（见表2，Arellano估计量。(0.087-0.091)/0.091=-0.043 96）。这表明在小样本情况下，依然有足够的理由使用聚类回归方法进行调整。另一方面，由于Fama-MacBeth方法在只存在固定时间效应时是无偏的，在确定面板数据中只存在时间效应时，可以用该方法进行调整。
    此外，很多作者在进行回归模拟时，引入了虚拟变量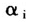，这说明作者考虑了数据中可能存在的个体效应。但是却很少有考虑时间效应的。如果数据中不存在个体效应，只存在时间效应，这样做往往不能得到正确的结果。如果同时存在个体效应和时间效应，使用仅仅能够吸收个体效应，并不能吸收时间效应。
    在上面的模拟中，由于事先设定了数据结构这便能够采用正确的方法处理数据。然而，实际中并不了解真实的数据结构。如果数据中只存在时间效应，却认为存在个体效应而采用了吸收个体效应的方法，或者同时存在两种效应，但是却只考虑了个体效应，又会出现什么情况呢？为了进一步分析方法使用错误而造成的偏误，基于上述模型，同时考虑了个体效应和时间效应
    
    
    表7是T为10年，N为250的模拟结果。可以看出，在存在时间效应时，即使很小（占比25%），使用消去个体效应的固定效应模型估计也会产生较大的偏差，而随着时间效应的增加，产生的偏误越来越大。尽管在模拟实验中显示，时间效应从25%增加到100%，Arellano估计量的偏误仅仅从95.52%增加到98.96%，增量似乎并不大，但是，25%的时间效应就足以产生95.52%的偏误，这就不得不重视实际数据中可能存在的时间效应。
    表7同时存在个体效应和时间效应情况下各种指数模拟结果（大样本）
    
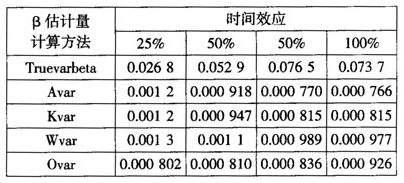
    注：时间T=10，个体N=250。
    表8是T为10年，N为50的模拟结果。与大样本情况类似，在存在时间效应时，使用消去个体效应的固定效应模型估计也会产生较大的偏差，并且偏误也随着时间效应的增加而增大。
    表8同时存在个体效应和时间效应情况下各种指数模拟结果（小样本）
    
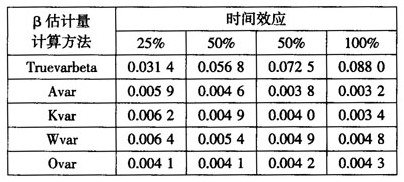
    注：间间T=10，个体N=50。
    1.3.2Fama-MacBeth误差估计
    同样对Fama-MacBeth方法的估计结果进行了比较，从表9可以看出，随着时间效应的增加，Fama-MacBeth方法估计的偏差迅速减小，当时间效应占总效应的一半时，Fama-MacBeth方法估计的误差只有4.17%。然而，如果时间效应较小而个体效应较大，估计仍有较大的偏误，本文认为这是个体效应造成的原因。上文已经说过，Fama-MacBeth方法不适合估计只存在个体效应的数据结构。
    表9同时存在个体效应和时间效应情况下Fama-MacBeth方法模拟结果
    
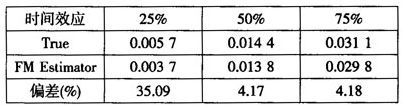
    注：时间T=10，个体N=250。
    1.3.3同时存在个体效应和时间效应的处理
    当同时存在个体效应和时间效应时，对回归系数的估计会复杂得多。在实际数据中，由于横向的公司数目N通常比纵向的时间数T大，实证研究常常在每一时期使用虚拟变量吸收时间效应，然后按照公司聚类进行回归。如果时间效应是固定的，那么使用时间虚拟变量可以完全吸收时间效应，在公司数日较大的情况下，可以得到较好的结果。
    Hsiao介绍了对同时存在个体效应和时间效应的面板数据估计方法。令
    
    最近，针对同时存在固定个体效应和固定时间效应的情况，Thompson[11]和Cameron等[12]提出了下面的估计方法
    
    2结束语
    众所周知，当面板数据中存在固定个体效应或者固定时间效应时，直接使用OLS估计的β标准差是有偏的。然而，部分实证论文并没有考虑数据中可能存在的固定个体效应或者固定时间效应，部分论文虽然考虑了固定效应，但在固定个体效应和固定时间效应的辨别上，往往是比较主观的，换言之，论文中并没有提供可信的证据来表明存在何种效应。本文通过模拟面板数据进行回归分析，证明了在数据中存在不同效应时，采用不合适的估计方法依然会产生较大的偏误。具体来说，本文比较了POOL OLS，固定效应模型和Fama-Macbeth方法在不同的数据结构中的处理结果，并且通过模拟可以看到，对某种数据结构，如果采用了不正确的方法，回归结果的偏差将会非常大
    尽管实证研究中选择正确的模型非常重要，但是，针对实际中面板数据的复杂性，研究中并没有针对模型选择的统一标准。特别是对于数据是否存在时间效应这一问题，实证中往往过于主观。通过本文的模拟，实际上为判断实际数据中存在何种效应提供了一种准则：即以OLS估计为基准，通过使用不同的模型进行估计，当固定个体效应模型估计与OLS估计结果有较大的偏差时，（见上文模拟结果和实证数据结果）有理由相信面板数据中存在个体效应；如果固定时间效应模型估计与OLS估计结果差别较大时，可以认为面板数据中存在时间效应；如果两种估计模型与OLS估计结果均有较大差别时，可以认为面板数据中同时存在个体效应和时间效应。这样，通过进一步了解实际中面板数据的结构，采用正确的估计方法，减少犯错的概率。
    在数据中只存在时间效应时，Fama-Macbeth方法能够产生无偏的β标准差。通过使用固定时间效应模型也能够产生无偏的结果，但是必须在时间数比较多的情况下才成立，如果时间数较少，用固定时间效应模型仍然会产生较大的偏误。但是，由于实际中往往存在样本过小的问题，特别是许多面板数据的时间维度往往过小。因此，如何在小样本下提供较为精确的判断准则，是本文今后将要关注和研究的问题。
    注释：
    ①ST是英文special treatment的缩写，意即“特别处理”。该政策自1998年4月22日起实行，针对的对象是出现财务状况或其他状况异常的上市公司。
    ②实证研究小POOL OLS亦较为常用，本文对OLS方法也进行了理论和模拟分析，以便对OLS方法和其他方法进行比较。
    ③面板数据估计模型分为变截距模型，变系数模型和联合回归模型3种。这里采用的是无截距的POOL OLS模型设定，一方面是因为本文的重点在于斜率标准差的估计问题，在固定效应模型中，截距并不是重要的估计量；另一方面，采用无截距的POOL OLS模型设定，可以使下文的推导更为简洁，并且不失一般性。
    ④panel data极限行为仅仅依赖于单位数N和时间长度T趋于无穷的方式。例如一种是固定N，让T趋于∞，接着N趋于∞，它们用（N,T趋于∞）表示：另一种是T=T(N)，表示T的大小受N控制，N趋于∞，T(N)趋于∞，记为（T(N),N趋于∞）：第3种是T、N分别趋于∞，没有相互约束，记为（N,T趋于∞）。这3种方式极限分别称为序贯、对角和联合极限。Phillips和Moon[9]主要对序贯极限理论和联合极限理论进行了研究，认为序贯极限在寻求极限行为快速渐近性上是有益的。即使在更强一些的条件下，联合极限理论也是很难得到并加以应用，但幸运的是，在所面临的T很大、N适中的情况下，联合极限理论研究和应用并没有多大困难。
    
    
    参考文献：
    [1]Kiefer N M. Estimation of fixed effect models for time series of cross-sections with arbitrary intertemporal covariance [J]. Journal of Econometrics, 1980,14(2):195-202.
    [2]White H A. Heteroscedasticity-consistent covariance matrix estimator and a direct test of heteroskedasticity[J]. Econometrica. 1984, 48(1):817-838.
    [3]Arellano M. Computing robust standard errors for within-groups estimators [J]. Oxford Bulletin of Economics and Statistic,1987, 49(4): 431-434.
    [4]Kezdi G. Robust standard error estimation in fixed-effects panel models[C]//Econometrics. EconWPA: 2004: 0508018.
    [5]Fama E, MacBeth. Risk, return and equilibrium: Empirical tests [J]. Journal of Political Economy, 1973, 81 (3): 607-636.
    [6]Newey W, Kenneth W. A simple, positive semi-definite, heteroscedastic and autocorrelation consistent covariance matrix[J]. Econometrica, 1987, 55(3):703-708.
    [7]Driscoll J C, Kraay A C. Consistent covariance matrix estimation with spatially dependent panel data[J]. Review of Economics and Statistics, 1998, 80( 1 ): 549-560.
    [8]Hsiao. Analysis of Panel Data [M]. Cambridge: Cambridge University Press, 2003.
    [9]Phillips P C B, Moon H R. Linear regression limit theory for nonstationary panel data[J]. Econometrica, 1999, 67 (1):1057-1111.
    [10]Petersen M A. Estimation standard errors in finance panel data sets: Comparing approaches[J]. Review of Financial Studies, 2007, 22 ( 1 ): 435- 480.
    [11]Thompson S. Simple formulas for standard errors that cluster by both firm and time [C] ?/Harvard working paper, Available at SSRN: 2006. http://ssrn. com/abstract = 914002.
    [12]Cameron A C, Gelbach J B, Miller D L. Robust inference with multi-way clustering[C]// University of California-Davis Working Paper No. 327, 2006.
    i附录
    简单证明如下.
    对于只存在时间效应的面板数据，有如下式子
    
    与只存在固定个体效应不同，在只存在固定时间效应时，使用时间维度进行分组以估计组内估计量，需要用到以下假设。
    
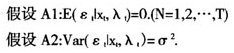
    如果假设A1成立而A2不成立.估计组内方差的普通回归公式将会产生不一致的标准误，该公式如下
    
    然而，既然