面板数据的分位回归方法及其模拟研究（一）

内容提要：文章讨论了含有固定效应的面板数据模型，给出了3种估计未知参数的分位回归方法，蒙特卡洛模拟结果显示这些分位回归方法是处理面板数据的有效手段，且在误差非正态时优于均值回归方法。文章最后给出了一个真实数据的建模案例，得到了有利于决策的有用参考信息。
    关键词：面板数据 固定效应 分位回归 蒙特卡洛模拟
    作者简介：罗幼喜，男，1979年生，湖北省红安县人，2005年毕业于华中师范大学概率论与数理统计专业，获理学硕士学位，现为湖北工业大学理学院讲师，中国人民大学统计学专业博士研究生，研究方向为数理统计及统计建模；田茂再，男，1969年生，湖南省人，2001年毕业于南开大学概率统计专业，获理学博士学位，现为中国人民大学统计学院教授，博士生导师，研究方向为数理统计。
    一、引言
    面板数据也称时间序列截面数据或混合数据，是一种同时在时间和截面空间上取得的二维数据，具有传统截面数据和时间序列方法所不具备的优势。
    面板数据虽有诸多好处，也被广泛应用于各个领域，但是存在着一定的局限性，一是传统的面板数据分析方法主要是基于服从正态分布的数据而做出的，然而一旦数据分布类型发生改变，这种传统的方法所作出的统计结论将不再可靠，而且我们目前也没有建立起一个衡量这种改变究竟会对最终结论带来多大风险的度量方法；二是传统的面板数据分析方法是一种条件均值模型，其主要目的只针对于估计和检验均值效应，然而数据的信息是全方位的，这种只对均值模型做估计和检验的方法虽然能够让研究者迅速掌握变量均值间可能存在的相互关系，但却忽略了数据其他方面的信息，没有能对数据的各个层次做一个全方位的刻画，遗漏了一些可能存在的重要信息，而这些信息往往是很多研究者在均值回归中难以发现的。
    为了改进传统面板数据分析方法的限制，本文考虑尝试将Koenker和Bassett(1978)提出的分位回归思想引入面板数据的分析之中。分位回归方法与传统均值回归方法不同，它是针对响应变量的条件分位函数进行统计推断的。首先这一方法的目标函数是加权的绝对偏差和，所以被估计的系数向量对响应变量的离群点并不敏感，当误差项服从非正态的时候，这种方法得到的估计量要比传统最小二乘估计量更可靠。其次这一方法在给定一组预测变量之后，能在任意分位点全面刻画响应变量的条件分布，给出数据各个层次间可能存在的重要信息，是对传统均值回归方法的一种有益改进和补充。
    Koenker(2004)考虑了纵向数据(Longitudinal Data)的分位回归方法，考虑将固定效应作为惩罚项的分位检验函数最小化估计方法，虽然蒙特卡洛模拟结果显示此方法在非正态分布情形下要优于传统的均值回归方法，但在每个个体层样本量较小的情况下该方法是很难得到有效的估计，且文献没有给出如何确定惩罚参数A取值的有效方法；Tian, Maozai and Chen, Gemai(2006)在正态假定下对分层线性模型提出了分层分位回归的思想，给出了一种新的迭代算法：EQ算法，考虑了EQ算法的渐近性质；Galvao(2008)提出了动态面板数据的分位回归方法，通过引入了工具变量减少遗漏变量带来的偏差，蒙特卡洛研究证实该方法在处理数据非正态和厚尾时比传统方法更具有优势；Galvao and Montes-Rojas(2009)同样引入工具变量讨论了含有测量误差的动态面板数据分位回归方法；Harding and Lamarche(2009)则利用工具变量解决了内生变量和个体效应与响应变量间相关时的面板数据分位回归方法；Powell(2009)讨论了含有外生或内生变量的面板数据的无条件分位回归方法，该方法的一个好处是能够有效估计固定效应参数并且其统计含义和横截面数据分位回归方法相同。纵观以上文献，目前关于面板数据的分位回归方法还处于一个起步阶段，有很多理论问题及方法需要探讨，也急需将这些已有研究成果应用于实际问题。本文正是在这方面做了一些有益探讨，文中给出了3种基于面板数据的分位回归方法，即一阶差分分位回归法、固定效应变换分位回归法和引进虚拟变量的惩罚分位回归法，并在不同误差分布情形下给出了3种方法同均值回归方法的蒙特卡洛模拟比较结果。最后利用分位回归的方法对我国各地区城镇居民人均收入与消费支出面板数据进行了建模分析，并根据分析结果提出了相应政策建议。
    二、模型及方法
    
    
    为检验函数，也称为损失函数，当τ=0.5时称为中位回归，也称为最小绝对偏差回归。然而，在实际问题中，我们面临的问题是往往N比较大但了却比较小，即对于每个个体而言，其观测值并不多，要想利用这少量的个体观测值去估计每个个体效应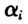并非易事，而且即使能够估计，其估计值也并非有效。考虑到大多数的研究中，参数值β才是人们的兴趣所在，所以我们的重点将放在对β的估计上。然而，如果在估计"的过程中完全忽略个体效应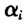，又会对最终的估计结果产生不利的影响，所以我们不能将所有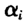看成是同一个数。那么如何消除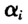的影响同时又能够得到β的有效估计呢，下面我们给出了3种方法。
    （一）一阶差分分位回归法
    
    可以获得β的τ分位点估计，称此估计为一阶差分分位回归估计FDQR(First-Differenced Quantile Regression Estimator)。
    （二）固定效应变换分位回归法
    下面我们考虑另外一种消除固定效应的方法。对每个i有，
    
    
    则求解此问题要涉及对高维设计阵的相关计算，不过好在此矩阵虽然维数很大，但很多元素为0，是个稀疏矩阵，这为我们的计算节省了不少时间。此方法能够同时给出回归系数β和固定效应参数的τ分位点估计，不过我们主要关注的是β的估计，称之为惩罚分位回归估计PQR(Penalized Quantile Regression Estimator)。
    与Koenker(2004)不同的是，我们没有采用多个分位点加权的目标函数，而且这里也假定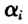是随分位点，的变化而变化的，而Koenker(2004)则将视为只与个体有关而与T无关的量。当然此方法面临的一个问题是当T较小时很难对每个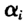在其各分位点处作出有效估计，幸好此处我们重点关心的是回归系数β的估计值，所以方法仍然可以实施。在模拟研究中，由于我们知道未知参数的真实值，所以可以选取使得偏差最小的λ作为惩罚参数值，但在实际问题中，由于未知参数并不知道，所以可以有多种方法和准则来确定λ的值，此处我们提出采用使得模型残差平方和最小的λ作为惩罚参数值的选取准则。
    需要特别指出的是，在上述3种方法中，只有PQR是同时给出了和β的估计，FOQR和FEQR虽然不能给出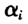的估计，但我们并没有忽略它可能对估计β造成的影响，因为进行一阶差分和固定效应变换都是在每个横截面单位内进行的，这实际上就是考虑到各个不同的横截面单位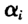的值是有所不同的，只有在同一个横截面单位内它们才是相同的。我们的条件分位函数都是建立在变换之后的模型式(4)和式(10)上的，所以如果要讨论β估计的大样本性质则还需要求变换后的模型中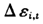和满足一定的条件，考虑到分位回归对误差项分布要求比较弱，所以在此我们并不对其作过多条件限制。不过在实际应用中另外一个值得注意的问题是此处要求解释变量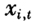应该随着时期t的不同而不同，否则可能会导致模型中参数β无法估计。

（未完待续）