会员登录
会员注册三、蒙特卡洛模拟
由于我们主要关心的参数为β，所以在本节的模拟中我们只给出"估计的结果。根据含固定效应面板数据结构设定产生模拟数据的模型为
①完全忽略个体固定效应，直接使用混合数据的普通最小二乘估计，记为LS估计；
②考虑个体固定效应的最小二乘估计，记为FE估计；
③完全忽略个体固定效应，直接使用混合数据的中位回归估计，记为QR估计；
④考虑个体固定效应的一阶差分中位回归估计，记为FDQR估计；
⑤考虑个体固定效应的固定效应变换中位回归估计，记为FEQR；
⑥考虑个体固定效应的带
惩罚项的中位回归估计，记为PQR。
其中①、②是传统的条件均值回归方法，③、④、⑤、⑥是条件分位回归方法。我们研究的目的是：
1.分位回归方法对于面板数据是否有效？
2.分位回归方法在估计的精度和稳定性上是否优于均值回归方法？
3.当模型中含有个体效应但却没有考虑时会产生何种影响。
4.当无法观测到的特异误差来自不同分布类型时哪种方法能有较好的表现。
从表1的结果来看，表现比较好的3种估计是PK、FDQR、FEQR，其中在估计偏差上FEQR法较小，但在估计的RMSE上，FE法是最小的，比较稳定。另外很明显的可以看出，完全忽略了个体效应的IS法和QR法其Bias和RMSE都很大，这也说明，即使是在误差正态的条件之下，不考虑面板数据中可能存在的个体效应而做出的估计会有很大的偏差和风险。另外PQR法虽然考虑了个体效应，但在时期数T太小时其偏差会比较大。
表1标准正态误差下6种估计的Bias和RMSE
从表2的结果来看，当误差具有厚尾分布时，显然分位回归方法FDQR和FEQR要优于传统的均值回归法，特别是FEQR法，不仅偏差很小，而且RMSE在所有情况下都是最小的，表现最为稳定。另外还可以看到，不考虑个体效应的QR法虽然表现很差，但在这种厚尾分布之下，比起同样不考虑个体效应的LS法，其Bias和RMSE均要小些。所以总的来看，当误差是对称厚尾分布时，分位回归方法较之均值回归方法在估计的精度和稳定性上都要占优。
表3的结果同表2差不多，其中表现最好的是FEQR法，特别是其Bias，在所有情况下绝对值均是最小的。其次是FE法和FDQR法，两方法的Bias和RMSE值都比较接近。另外在这种偏态的误差分布下，QR法较LS法更为有效些。
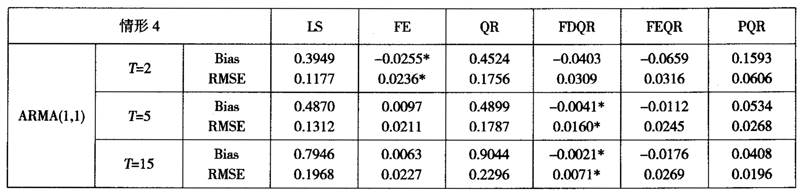
当误差是序列相关时，仅在T=2时FE法优于FDQR法，而在其他情况下，FDQR法都是最优的，这说明对数据在相邻期上进行一阶差分可以在一定程度上消除这种误差相关性对参数估计所带来的不利影响。
综合以上所有模拟结果显示：
1.在模型判断正确的情况下，分位回归方法是处理面板数据的一种有效手段，能够对回归参数做出精确稳定的估计。
2.当模型满足误差正态条件假设时，分位回归方法与传统均值回归方法相当，只在稳定性上略差一点，但当模型不是正态误差时，则分位回归方法比均值回归方法在估计精度和稳定性上都好，特别是厚尾和偏态误差时，其优良性较为明显。
3.不管是均值回归法还是分位回归法，如果对面板数据中存在的个体效应完全忽略，都会给估计值带来较大的偏差，而且估计也会变得不够稳定。
表2t分布误差下6种估计的Bias和RMSE
表3卡方分布误差下6种估计的Bias和RMSE
表4序列相关误差下6种估计的Bias和RMSE
所以对于一个实际面板数据而言，判断是否存在固定效应将是一个非常重要的工作，好在这一点可以借助于一些已有的检验方法来实现，如固定效应的似然比检验法等。
4.当误差为正态分布时，FE法有较好的表现，当误差呈现厚尾或偏态分布时，FEQR法有较好的表现，当误差具有序列相关性时，FDQR法有较为良好的表现。
上述模拟中我们只考虑了当模型的误差分布发生变化时各种方法的估计效果比较，然而实际上模型的其他参数值
以及截距a也可能会影响到β的估计，所以下面我们就考虑对这几种估计方法在不同的模型参数初始值设定时进行模拟比较研究。为了使结果具有可比性，我们依次改变其中的一个参数值而保持其他参数值不变。为节省篇幅，下面只给出当误差服从标准正态分布且N=30，T=5时的模拟结果。
对表5的结果进行比较不难发现截距a的改变对各种估计方法几乎没有什么影响，
虽然影响大些，但主要是对LS法、QR法和PQR法影响较大，对本文新提出的FDQR法和FEQR法影响并不明显，更重要的是这两种方法在所有不同参数初始值设定情况下都有着比较小的Bias和RMSE，这就意味着我们提出FDQR法和FEQR法对不同的固定效应模型都能适用。
表5不同初始值时6种估计的Bias和RMSE
(未完待续）