会员登录
会员注册三、数据选取与处理
根据研究目的，本文选取了上证A股招商银行(600036)2009年8月3日到2010年7月30日共235个交易日的日数据、5分钟数据和分笔数据，分别对应低频、高频、超高频数据。其中，对于分笔数据，剔除了连续竞价时间段外的所有交易数据，还剔除了跨天交易持续期和下午开盘第一个交易持续期，并对交易间隔为0的数据项进行合并，交易量相加，价格按照交易量加权平均。表1为招商银行收益率和持续期的描述统计。
表1招商银行收益率和持续期的描述统计
注：收益率的均值和标准差均已扩大了1000倍。
从表1可以看出，一笔交易的持续期平均为5秒左右。5分钟收益率和超高频收益率均拒绝了JB的正态假设。Lijung-Box的20阶检验显示，5分钟收益率、超高频收益率和交易间隔都具有高度和长期的自相关性。
超高频数据在日内表现出稳定的周期性运动模式，称为日历效应。图1为招商银行持续期的日内波动特征图，从图中可以看出，招商银行1天内收益率的波动呈现倒U型模式，开盘和收盘的交易间隔较小，中间时段的交易间隔较大。为了剔除超高频数据的日历效应，根据Engle和Russell(1998)的研究，本文采用样条函数插值法对时间间隔和日内周期变化特征进行分析，将线性样条函数按9:30、10:00、11:00、13:00、14:00、14:30、15:00划分为六个交易时间段进行拟合。后面使用的持续期序列xi都是剔除了日内周期特征的数据。
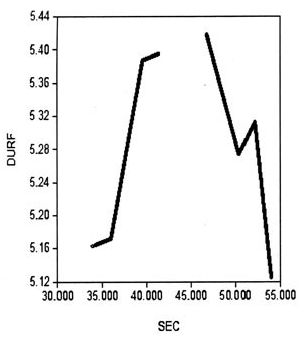
图1招商银行交易持续期日内波动特征
四、实证分析及结论
（一）APARCH模型的估计结果
对于低频日收益率数据，本文基于偏学生分布分别估计了GARCH和APARCH两种模型。通过估计两模型参数进而计算出每天的条件波动，结合收益率的分位数，最终计算出了金融资产1天的VaR。
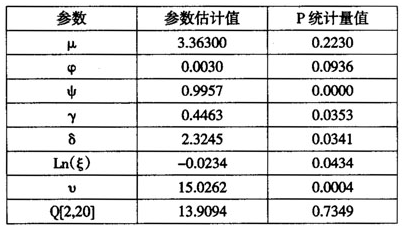
限于篇幅，我们仅给出APARCH模型的方差方程的估计结果（见表2）。从表2可以看出：(1)偏度系数Ln（ξ）＜0，且通过了5%的显著性水平检验，说明随机变量vt序列分布左偏，这与基本统计检验相吻合；(2)γ＞0且显著，表明存在较为明显的杠杆作用（条件方差的不对称性），即负的收益率比正的收益率产生了更大的波动；(3)自由度v显著大于2，说明分布呈现厚尾形态。另外，从残差序列统计检验Q220所表现出的显著性水平可以发现，这里采用的ARMA(1，1)-APARCH(1，1)-SKST模型较好地刻画了日收益率序列的尖峰厚尾及不对称特征。
表2APARCH-SKST模型的估计结果
因此，通过模型ARMA(1，1)-APARCH(1，1)-SKST的参数估计，可以得到日收益率的条件波动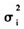
，进而得到未来1天的APARCH条件波动率预测值和金融资产的VaR。
（二）UHF-GARCH模型的估计结果
本文经过反复试验，确定使用残差服从正态分布的UHF-EGARCH(1，1)模型对剔除日内效应的分笔收益率进行刻画，均值方程采用ARMA(1，1)形式，其中EGARCH(1，1)模型部分为：
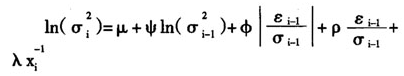
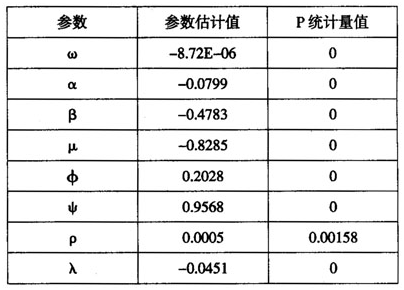
模型的参数估计结果见表3。由表3可以看出，模型各参数均在1%的水平下显著。φ+ψ＞1说明剔除日历效应的超高频收益率的GARCH效应与低频数据一样强，也说明使用UHF-GARCH模型能够很好地刻画超高频收益率。ρ＞0说明利好消息比利空消息导致了更大的波动。此外，
的系数λ为负，说明交易间隔时间越长，波动率越大，这与Diamond和Verrechia(1987)的结论相似。
表3UHF-EGARCH模型的估计结果
（三）RV和UHFV模型的估计结果
前文由UHF-EGARCH模型计算得到的条件波动是日内单位时间的波动率，而目前金融风险管理一般计算的是1天层次的波动率，因此，需要按照公式(13)把UHF-EGARCH模型计算得到的条件波动按天进行加总，即可得到1天层次的超高频波动率UHFV。
此外，使用招商银行5分钟数据，根据公式(5)，可以计算出1天层次的已实现波动率RV。由于RV和UHFV都使用了日内交易信息，因此比低频数据包含了更多的信息，但这些信息是否有助于提高金融风险价值的计算精度，还有待于进行深入的对比分析。
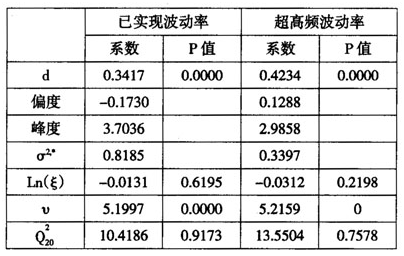
从表4可以看出，招商银行RV序列和UHFV序列均呈现右偏分布，且具有明显的尖峰厚尾特征，两序列的JB检验都拒绝了序列正态性的假设。Ljung-Box的20阶检验结果显示，RV和UHFV序列在1%的显著性水平下拒绝了不存在自相关的零假设，说明已实现波动和超高频波动均具有显著的长记忆性。取对数后的RV和UHFV近似服从正态分布。
表4已实现波动率与超高频波动率的描述统计
表5条件波动调整后的收益率拟合
2.Dynamic quantile regression检验。在检验VaR的精度时，除了kupiec检验外，Engle等(2004)[12]还提出了动态分位数回归检验方法。如果VaR失败的观察值之间具有明显的相关性，则有可能发生连续超过VaR的损失。这种情况一旦发生，给金融市场带来的风险将成倍加大。事实证明，这种事件的发生往往会伴随着金融资产价格波动的加剧以及金融风险的暴露，甚至金融危机的发生。为了能够在进行失败率检验的同时进行VaR相关性检验，Engle等提出了Dynamic quantile regression检验方法，即首先构造一个新的碰撞序列
表7给出了各模型动态分位数检验的P值，这里选择q=5作为动态分位数回归检验变量选择的标准。
表6Kupiec似然比检验结果
注：表中数据为kupiec LR检验的P值，P值越大，表明收益分布模型计算的VaR精确度越高；表中上半部分为正态分布模型，下半部分为偏学生分布模型。
表7动态分位数检验结果
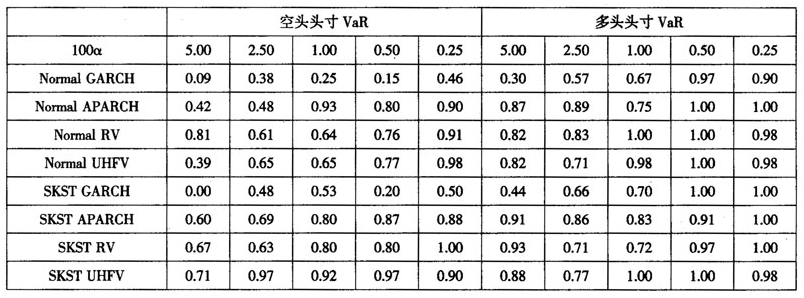
3.结果分析。(1)基于GARCH模型计算的金融风险虽然在实际中使用较多，但该方法很难精确计算VaR值。在40组检验中，有5组数据的p值检验拒绝了GARCH模型的VaR估计结果，并且出现了低于5%、甚至1%的p值。这也说明，在国外经常使用的方法或模型，并不一定适合我国的金融市场。
(2)对比GARCH模型和APARCH模型的检验结果可以发现，使用APARCH模型计算得到的VaR精度有了很大提高，在显著性水平较高时，也能够很好地刻画金融风险。
(3)基于RV模型的VaR回测检验结果显示，已实现波动率能够准确衡量金融风险，在显著性水平较高时表现较好，优于APARCH模型，但在显著性水平较低时衡量的准确性不如APARCH模型。在40组检验中，有20组结果显示RV模型优于APARCH模型，有16组结果显示APARCH模型优于RV模型。总的来说，两模型计算VaR精度的差距很小。
(4)基于UHFV模型计算VaR的结果显示，超高频波动率计算VaR的精度稍微优于RV和APARCH模型，但差距很小。在40组检验中，UHFV模型有22组优于RV模型，RV模型有10组优于UHFV模型；UHFV模型有24组优于APARCH模型，APARCH模型有14组优于UHFV模型。但是，这并不能说明UHFV模型比另外两个模型在测量金融风险精确度方面更好，原因在于，在大多数分位数上，UHFV模型的p值并不是显著大于另外两个模型的p值，它们之间的差距大多只有0.01～0.05，UHFV模型也存在很多p值较小的情况。综合看来，虽然高频数据和超高频数据包含了更多的日内信息，能够反映更多的实际交易情况，但从预测精度上看，基于高频和超高频数据的模型并没有显著提高金融风险的预测准确度，而使用低频数据，只要模型设定适当，仍然能够较为准确地描述金融市场的风险。
(5)对比基于正态分布模型和偏学生分布模型可以发现，无论是在高显著水平还是在低显著水平上，偏学生分布模型都比正态分布模型能够更加准确地描述金融风险。在全部80组对比数据中，SKST模型有52组数据优于Normal模型，Normal模型有21组数据优于SKST模型。这说明，消除了条件波动的收益率不服从正态分布，使用SKST模型能够更加精准地描述金融风险。
五、结论及高频数据的适用性分析
目前对金融高频数据的分析方法只是低频数据方法的扩展和移植，还不完善，使用高频数据甚至超高频数据测量金融风险的准确性并不比低频数据高很多。也就是说，如果我们选用恰当的模型，完全能够使用低频数据得到高频数据的精度，还可以省去很多高频数据获取、处理等的成本和不便。既然高频数据的使用并不能显著提高金融风险计量的精度，那么，是否不需要使用高频数据？这就要对高频数据的优缺点及适用性进行分析。
高频数据在衡量金融风险时有诸多优势。风险分析只有在相当大的样本下才能显示出有效性，高频数据包含了更多的信息，能够提供更丰富的数据资源。所谓“大样本”往往是成千上万，日数据、周数据、月度数据等低频数据都难以满足大样本的要求[13]。我国股市建立至今也只积累了大概5000个日数据样本，周数据需要100年才能达到5000个左右，而400年的月度数据才能累计约5000个样本。很显然，即使是成熟市场（如纽约证券市场能提供100年的数据），也很难提供如此多的数据资料。即便能提供，但在如此长的时间内，这些数据在各个历史阶段会具有不同的特征，是否有可比性值得怀疑。如果分阶段分析，那么“大样本”性质又得不到满足。伴随着存储技术的进步，金融市场的高频数据被完整地记录下来，这为金融实证分析提供了充足的数据资源。以5分钟数据为例，只要5个月时间即可得到5000个样本，而对于1分钟数据，只需要21天就能得到5000个样本。高频数据倍受瞩目的原因还在于，金融高频数据和超高频数据对理解金融市场的微观结构是相当重要的。高频数据在计算金融风险时有很多优势，但是也存在一些问题。例如，高频数据的获取成本很高；高频数据处理方法复杂，数据文件超大（招商银行一年的分笔数据excel文件有80M），程序运行耗费时间较多；高频数据模型仍然处于探索阶段，目前只是低频数据模型的移植和扩展，未有突破性进展，使用目前的高频数据模型计算金融风险并不能显著提高测度的准确性。
鉴于高频数据存在的这些问题，目前计算金融风险时并不一定非要使用高频数据，但有三类金融风险管理者可以使用高频数据来对风险进行计量。一是对预测精度要求高的用户。高频数据模型虽然不是很完善，但确实有助于提高金融风险的预测精度。虽然个别低频数据模型也能达到高频数据的预测精度，但毕竟还有差距，而且并不是每个低频数据模型都能达到高频数据模型的计算精度。二是短期测度时可以使用高频数据。短期内预测时往往使用的是近期数据，低频数据很难达到大样本要求，这时使用高频数据有很大的优势，预测精度会提高很多。由于时期比较短，因此也不存在数据处理的难度问题。三是对成本、时间需求弹性小的用户可以使用高频数据。高频数据不但获取成本高，而且处理成本也很高。高频数据量往往很大，单个数据文件即可达百兆，必须要高端机器才能运行。另外，处理数据需要一定的时间，如果风险管理者对数据成本和处理时间需求弹性不大，则可以考虑使用高频数据。
参考文献：
[1]Andersen T G, T Bollerslev, N Meddahi. Analytical Evaluation Of Volatility Forecasts[J]. International Economic Review, 2004(45):1079-1110.
[2]Pierre Giot S L.Market risk in commodity markets: a var approach[J]. Forthcoming in Journal of Futures Markets, 2002(1).
[3]Martens M,Dvan Dijk. Measuring volatility with the realized range[J]. Journal of Econometrics, 2007(138).
[4]黄后川，陈浪南.中国股票市场波动率的高频估计与特性分析[J].经济研究，2003(2):75-94.
[5]邵锡栋，连玉君，黄性芳.交易间隔、超高频波动率与VaR——利用日内信息预测金融市场风险[J].统计研究，2009(1):96-102.
[6]Dionne G,P Duchesne, M Pacurar. Intraday Value at Risk (IVaR) using tick-by-tick data with application to the Toronto Stock Exchange[J]. Journal of Empirical Finance, 2005,16(5):777-792.
[7]Matsumoto T, et al. The Quality of Life Questionnaire for Cancer Patients Treated with Anticancer Drugs (QOL-ACD): Validity and Reliability in Japanese Patients with Advanced Non-Small-Cell Lung Cancer[J]. Qual Life Res, 2002,11(5):483-493.
[8]Andersen T G, et al. The Distribution of Realized Exchange Rate Volatility[J]. Journal of the American statistical association, 2001(3):42-55.
[9]Giot P L S. Modeling daily value-at-risk usingrealized volatility and ARCH type models[J]. Journal of Empirical Finance, 2004(11):379-398.
[10]Racicot F.Forecasting Irregularly Spaced UHF Financial Data: Realized Volatility vs UHF-GARCH Models[J]. International Advances in Economic Research, 2008,14(1):112-124.
[11]P K. Techniques for verifying the accuracy of risk meeasurement models[J]. Journal of Derivatives, 1995(2):173-184.
[12]Engle R F, S Manganelli. CAViaR: Conditional autoregressive value at risk by regression quantiles[J]. Journal of Business & Economic Statistics, 2004,22(4):367-381.
[13]尹优平，马丹.基于分布拟合方法的高频数据风险价值研究[J].金融研究，2005(3):59-67.